Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn và trải nghiệm website không quảng cáo
Tìm hiểu thêm »Giải Toán lớp 5 trang 9, 10, 11 sách Cánh diều tập 2 giúp các em học sinh lớp 5 tham khảo, xem gợi ý giải các bài tập Bài 52: Hình thang của Chương III: Hình học và đo lường để ngày càng học tốt môn Toán 5.
Giải SGK Toán 5 trang 9 → 11 Cánh diều tập 2 được biên soạn chi tiết, bám sát nội dung trong sách giáo khoa. Đồng thời, cũng giúp thầy cô tham khảo để soạn giáo án cho học sinh của mình theo chương trình mới. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:
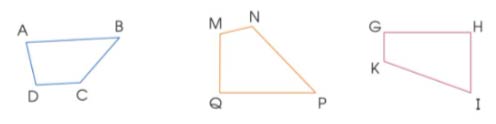
Trong các hình sau, hình nào là hình thang? Hãy chỉ ra cặp cạnh đáy, cặp cạnh bên của mỗi hình thang đó.
Lời giải:
- Trong các hình, hình ABCD, GHIK là hình thang.
- Hình thang ABCD có:
+ Cạnh đáy AB và cạnh đáy DC.
+ Cạnh bên AD và cạnh bên BC.
- Hình thang GHIK có:
+ Cạnh đáy GK và cạnh đáy HI.
+ Cạnh bên GH và cạnh bên KI.
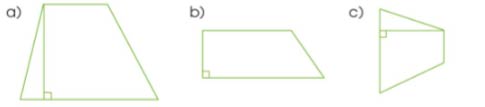
Đo chiều cao của mỗi hình thang sau:
Lời giải:
a) Chiều cao là 3 cm.
b) Chiều cao là 1,5 cm.
c) Chiều cao là 2 cm.
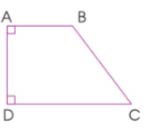
a) Hình thang ABCD có những góc nào là góc vuông? Cạnh bên nào vuông góc với hai đáy?
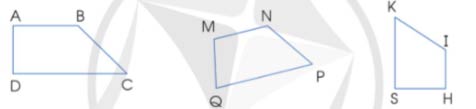
b) Chỉ ra hình thang vuông trong các hình thang sau:
Lời giải:
a) Hình thang ABCD có góc đỉnh A và góc đỉnh D là góc vuông.
Cạnh bên AD vuông góc với hai đáy.
b) Hình thang vuông ABCD, hình thang vuông KIHS
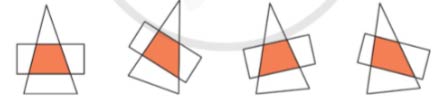
a) Lấy một mảnh giấy hình chữ nhật và một mảnh giấy hình tam giác đặt chồng lên nhau. Quan sát và nói cho bạn nghe phần chồng lên nhau của hai mảnh giấy có hình dạng như thế nào.
b) Cắt hai hình thang giống nhau, rồi ghép thành một hình bình hành.

Nhận xét về mối liên hệ giữa độ dài hai đáy của hình thang với cạnh của hình bình hành.
c) Kể một số vật trong thực tế có dạng hình thang.
Lời giải :
a) Phần chồng lên nhau của hai mảnh giấy có hình dạng hình thang.
b) Nhận xét: Tổng độ dài hai đáy của mỗi hình thang bằng cạnh của hình bình hành.
c) Một số vật trong thực tế có dạng hình thang là: cái thang, mặt túi xách, thùng rác, túi đựng bỏng ngô,...
a) Chỉ ra cách vẽ thêm hai đoạn thẳng trong mỗi hình sau để được một hình thang:
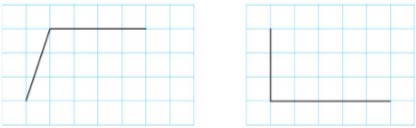
b) Chỉ ra cách vẽ thêm một đoạn thẳng trong hình sau để được một hình bình hành và một hình tam giác:

Lời giải:
a) Hình thang có một cặp cạnh đối diện song song. Ta có thể vẽ như sau:
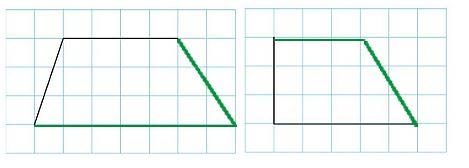
b) Hình bình hành có hai cặp cạnh đối diện song song và bằng nhau. Ta có thể vẽ như sau:
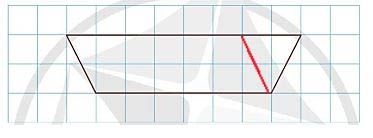
a) Vẽ mỗi hình sau vào vở (theo mẫu):
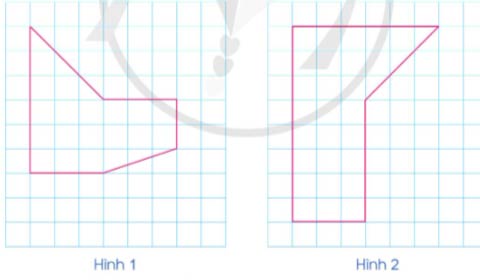
b) Vẽ thêm một đoạn thẳng trong hình 1 để được hai hình thang.
c) Vẽ thêm một đoạn thẳng trong hình 2 để được một hình thang và một hình tam giác.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: