Toán lớp 5 Bài 4: Ôn tập và bổ sung về phân số Giải Toán lớp 5 Cánh diều tập 1 trang 12, 13, 14

Giải Toán lớp 5 trang 12, 13, 14 sách Cánh diều tập 1 giúp các em học sinh lớp 5 tham khảo, xem gợi ý giải các bài tập Bài 4: Ôn tập và bổ sung về phân số của Chương I: Ôn tập và bổ sung về số tự nhiên, phân số, số thập phân để ngày càng học tốt môn Toán 5.

Giải SGK Toán 5 trang 12 → 14 Cánh diều tập 1 được biên soạn chi tiết, bám sát nội dung trong sách giáo khoa. Đồng thời, cũng giúp thầy cô tham khảo để soạn giáo án cho học sinh của mình theo chương trình mới. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Download.vn:

Toán 5 Ôn tập và bổ sung về phân số Cánh diều

Giải Toán 5 Cánh diều Tập 1 trang 12, 13, 14 - Luyện tập, Thực hành
Giải Toán 5 Cánh diều Tập 1 trang 14 - Vận dụng
- Bài 8

Giải Toán 5 Cánh diều Tập 1 trang 12, 13, 14 - Luyện tập, Thực hành

Bài 1

Trò chơi “Ghép thẻ”

a) Ghép các thẻ ghi phân số thích hợp với thẻ hình vẽ có số phần đã tô màu tương ứng:

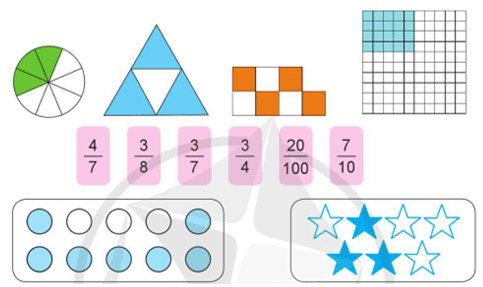
Ôn tập và bổ sung về phân số

b) Đọc các phân số ở câu a và nêu tử số, mẫu số của mỗi phân số đó.

Lời giải:

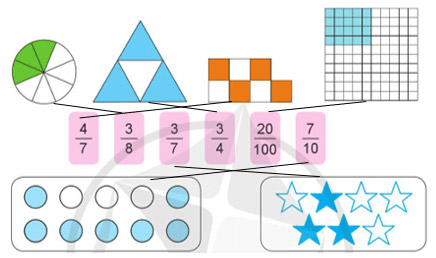
Ôn tập và bổ sung về phân số

$\frac{4}{7}$ đọc là: bốn phần bảy; tử số là 4, mẫu số là 7

$\frac{3}{8}$ đọc là: ba phần tám; tử số là 3, mẫu số là 8

$\frac{3}{7}$ đọc là: ba phần bảy; có tử số là 3, mẫu số là 7

$\frac{3}{4}$ đọc là: ba phần tư; tử số là 3, mẫu số là 4

$\frac{20}{100}$ đọc là: hai mươi phần một trăm; tử số là 20, mẫu số là 100

$\frac{7}{10}$ đọc là: bảy phần mười; tử số là 7, mẫu số là 10

Bài 2

a) Viết phân số chỉ số phần đã tô màu trong mỗi hình rồi đọc (theo mẫu):

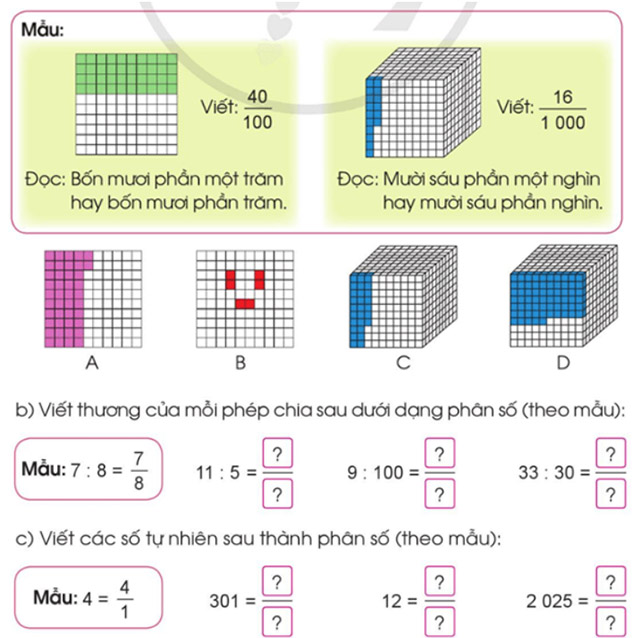
Ôn tập và bổ sung về phân số

Lời giải:

a) Hình A

Viết $\frac{42}{100}$

Đọc: Bốn mươi hai phần một trăm hay bốn mươi hai phần trăm

b) Hình B

Viết $\frac{6}{100}$

Đọc: Sáu phần một trăm hay sáu phần trăm

c) Hình C

$\frac{27}{1000}$

Đọc: Hai mươi bảy phần một nghìn hay hai bảy phần nghìn

d) Hình D

$\frac{65}{1000}$

Đọc: Sáu mươi lăm phần một nghìn hay sáu mươi lăm phần nghìn

11 : 5 = $\frac{11}{5}$

9 : 100 = $\frac{9}{100}$

33 : 30 = $\frac{33}{30}$

c) Viết các số tự nhiên sau thành phân số (theo mẫu):

Mẫu: $4\ =\ \frac{4}{1}$

301 = $\frac{301}{1}$

12 = $\frac{12}{1}$

2 025 = $\frac{2025}{1}$

Bài 3

a) Nêu hai phân số bằng mỗi phân số sau: $\frac{5}{4};\,\frac{9}{{12}}$ .

b) Rút gọn các phân số sau: $\frac{{24}}{{32}};\,\,\frac{{14}}{{35}};\,\,\frac{{30}}{{25}};\,\,\frac{{63}}{{36}}$

Lời giải:

a) $\frac{5}{4} = \frac{{5 \times 3}}{{4 \times 3}} = \frac{{15}}{{12}} ; \frac{5}{4} = \frac{{5 \times 5}}{{4 \times 5}} = \frac{{25}}{{20}}$

Hai phân số bằng phân số $\frac{5}{4}$ là $\frac{{15}}{{12}}$ và $\frac{{25}}{{20}}$

$\frac{9}{{12}} = \frac{{9:3}}{{12:3}} = \frac{3}{4} ; \frac{9}{{12}} = \frac{{9 \times 2}}{{12 \times 2}} = \frac{{18}}{{24}}$

Hai phân số bằng phân số là $\frac{9}{{12}}$ là $\frac{3}{4}$ và $\frac{{18}}{{24}}$

b) $\frac{{24}}{{32}} = \frac{{24:8}}{{32:8}} = \frac{3}{4}$

$\frac{{14}}{{35}} = \frac{{14:7}}{{35:7}} = \frac{2}{5}$

$\frac{{30}}{{25}} = \frac{{30:5}}{{25:5}} = \frac{6}{5}$

$\frac{{63}}{{36}} = \frac{{63:9}}{{36:9}} = \frac{7}{4}$

Bài 4

Quy đồng mẫu số hai phân số:

Ôn tập và bổ sung về phân số

Lời giải:

a) $\frac{4}{7} = \frac{{4 \times 2}}{{7 \times 2}} = \frac{8}{{14}}$ ; giữ nguyên phân số $\frac{3}{{14}}$ .

Vậy quy đồng mẫu số hai phân số $\frac{3}{{14}}$ và $\frac{4}{7}$ ta được $\frac{3}{{14}}$ và $\frac{8}{{14}}$ .

b) $\frac{2}{3} = \frac{{2 \times 2}}{{3 \times 2}}$ = $\frac{4}{6}$ ; giữ nguyên phân số $\frac{5}{6}$ .

Vậy quy đồng mẫu số hai phân số $\frac{2}{3}$ và $\frac{5}{6}$ ta được $\frac{4}{6}$ và $\frac{5}{6}$ .

Bài 5

a) Đọc ví dụ sau rồi nói cho bạn nghe cách thực hiện:

Ví dụ: Quy đồng mẫu số hai phân số $\frac{2}{3}$ và $\frac{5}{4}$

Vì 3 x 4 = 12 nên ta chọn 12 làm mẫu số chung.

Ta có: $\frac{2}{3} = \frac{{2 \times 4}}{{3 \times 4}} = \frac{8}{{12}} và \frac{5}{4} = \frac{{5 \times 3}}{{4 \times 3}} = \frac{{15}}{{12}}$

Vậy quy đồng mẫu số hai phân số $\frac{2}{3}$ và $\frac{5}{4}$ ta được $\frac{8}{12}$ và $\frac{{15}}{{12}}$

b) Quy đồng mẫu số hai phân số:

Ôn tập và bổ sung về phân số

Lời giải:

a) Cách quy đồng mẫu số:

- Chọn mẫu số chung

- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.

- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.

$\frac{1}{4}$ và $\frac{5}{3}$

Vì 4 x 3 = 12 nên ta chọn 12 làm mẫu số chung.

Ta có: $\frac{1}{4} = \frac{{1 \times 3}}{{4 \times 3}} = \frac{3}{{12}} và \frac{5}{3} = \frac{{5 \times 4}}{{3 \times 4}} = \frac{{20}}{{12}}$

Vậy quy đồng mẫu số hai phân số $\frac{1}{4}$ và $\frac{5}{3}$ ta được $\frac{3}{{12}}$ và $\frac{{20}}{{12}}$ .

$\frac{3}{5}$ và $\frac{4}{7}$

Vì 5 x 7 = 35 nên ta chọn 35 làm mẫu số chung.

Ta có: $\frac{3}{5} = \frac{{3 \times 7}}{{5 \times 7}} = \frac{{21}}{{35}}$ và $\frac{4}{7} = \frac{{4 \times 5}}{{7 \times 5}} = \frac{{20}}{{35}}$

Vậy quy đồng mẫu số hai phân số $\frac{3}{5}$ và $\frac{4}{7}$ ta được $\frac{21}{35}$ và $\frac{20}{35}$ .

$\frac{3}{{10}}$ và $\frac{7}{9}$

Vì 10 x 9 = 90 nên ta chọn 90 làm mẫu số chung.

Ta có: $\frac{3}{{10}} = \frac{{3 \times 9}}{{10 \times 9}} = \frac{{27}}{{90}}$ và $\frac{7}{9} = \frac{{7 \times 10}}{{9 \times 10}} = \frac{{70}}{{90}}$

Vậy quy đồng mẫu số hai phân số $\frac{3}{10}$ và $\frac{7}{9}$ ta được $\frac{{27}}{{90}}và \frac{{70}}{{90}}$

Bài 6

Quy đồng mẫu số hai phân số:

Ôn tập và bổ sung về phân số

Lời giải:

+) $\frac{3}{4}$ và $\frac{1}{6}$

Chọn 12 làm mẫu số chung.

Ta có: $\frac{3}{4} = \frac{{3 \times 3}}{{4 \times 3}}$ = $\frac{9}{{12}}$ và $\frac{1}{6} = \frac{{1 \times 2}}{{6 \times 2}} = \frac{2}{{12}}$

Vậy quy đồng mẫu số hai phân số $\frac{3}{4}$ và $\frac{1}{6}$ ta được $\frac{9}{12}$ và $\frac{2}{12}$

+) $\frac{7}{10}$ và $\frac{5}{8}$

Chọn 40 làm mẫu số chung.

Ta có: $\frac{7}{{10}} = \frac{{7 \times 4}}{{10 \times 4}} = \frac{{28}}{{40}}$ và $\frac{5}{8} = \frac{{5 \times 5}}{{8 \times 5}} = \frac{{25}}{{40}}$

Vậy quy đồng mẫu số hai phân số $\frac{7}{10}$ và $\frac{5}{8}$ ta được $\frac{28}{40}$ và $\frac{25}{40}$ .

+) $\frac{4}{9}$ và $\frac{5}{{16}}$

Chọn 144 làm mẫu số chung.

Ta có: $\frac{4}{9} = \frac{{4 \times 16}}{{9 \times 16}} = \frac{{64}}{{144}}$ và $\frac{5}{{16}} = \frac{{5 \times 9}}{{16 \times 9}} = \frac{{45}}{{144}}$

Vậy quy đồng mẫu số hai phân số $\frac{4}{9}$ và $\frac{5}{{16}}$ ta được $\frac{64}{144}$ và $\frac{{45}}{{144}}$ .

Bài 7

>, <,= ?

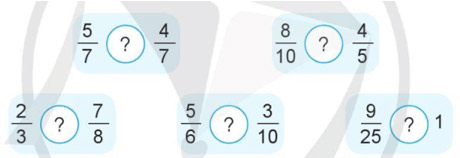
Ôn tập và bổ sung về phân số

b) Sắp xếp các phân số $\frac{2}{3}$ ; $\frac{6}{7}$ ; $\frac{3}{4}$ theo thứ tự từ bé đến lớn.

Lời giải:

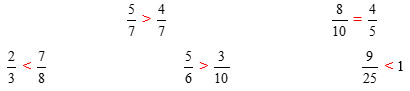
Ôn tập và bổ sung về phân số

b) Chọn mẫu số chung là 84.

Ta có $\frac{2}{3} = \frac{{2 \times 28}}{{3 \times 28}} = \frac{{56}}{{84}}$

$\frac{6}{7} = \frac{{6 \times 12}}{{7 \times 12}} = \frac{{72}}{{84}}$

$\frac{3}{4} = \frac{{3 \times 21}}{{4 \times 21}} = \frac{{63}}{{84}}$

Vì $\frac{{56}}{{84}} < \frac{{63}}{{84}} < \frac{{72}}{{84}}nên \frac{2}{3} < \frac{3}{4} < \frac{6}{7}.$

Vậy các phân số đã cho viết theo thứ tự từ bé đến lớn là $\frac{2}{3}$ ; $\frac{3}{4}$ ; $\frac{6}{7}$ .

Giải Toán 5 Cánh diều Tập 1 trang 14 - Vận dụng

Bài 8

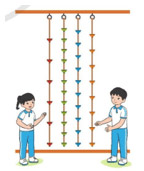
Dung và Đức cùng tham gia trò chơi leo dây với các dây có cùng chiều dài. Dung leo được $\frac{5}{8}$ sợi dây. Đức leo được $\frac{4}{10}$ sợi dây.