Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn (không bao gồm tài liệu cao cấp) và trải nghiệm website không quảng cáo
Tìm hiểu thêm »Giải Toán lớp 12 tập 1 trang 50, 51 Chân trời sáng tạo là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 12 tham khảo.
Giải Toán 12 Chân trời sáng tạo bài 1 Vectơ và các phép toán trong không gian được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 50, 51. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán 12 tập 1 bài 1 Vectơ và các phép toán trong không gian, mời các bạn cùng theo dõi tại đây.
Cho hình hộp ABCD.A′B′C′D′. Chứng minh rằng:
a)  \(\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {AC'}\)
\(\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {AC'}\)
b)  \(\overrightarrow {DB'} + \overrightarrow {D'D} + \overrightarrow {BD'} = \overrightarrow {BB'}\)
\(\overrightarrow {DB'} + \overrightarrow {D'D} + \overrightarrow {BD'} = \overrightarrow {BB'}\)
c)  \(\overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {DB} + \overrightarrow {C'D} = \overrightarrow 0\)
\(\overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {DB} + \overrightarrow {C'D} = \overrightarrow 0\)
Hướng dẫn giải:
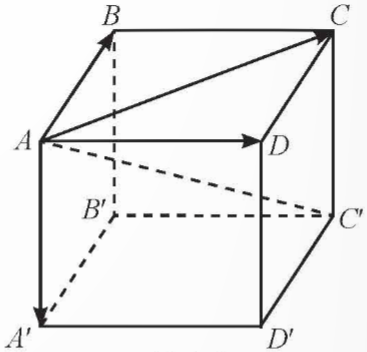
a) Ta có:  \(\overrightarrow{B'C'}=\overrightarrow{AD};\ \overrightarrow{DD'}=\overrightarrow{AA'}\)
\(\overrightarrow{B'C'}=\overrightarrow{AD};\ \overrightarrow{DD'}=\overrightarrow{AA'}\)
Áp dụng quy tắc hình hộp, ta có:
 \(\overrightarrow{AB}+\overrightarrow{B'C'}+\overrightarrow{DD'}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC'}\)
\(\overrightarrow{AB}+\overrightarrow{B'C'}+\overrightarrow{DD'}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC'}\)
b) Ta có:  \(\overrightarrow{DB'}+\overrightarrow{D'D}+\overrightarrow{BD'}\)
\(\overrightarrow{DB'}+\overrightarrow{D'D}+\overrightarrow{BD'}\)
 \(=\overrightarrow{DB'}+\left(\overrightarrow{BD'}+\overrightarrow{D'D}\right)\)
\(=\overrightarrow{DB'}+\left(\overrightarrow{BD'}+\overrightarrow{D'D}\right)\)
 \(=\overrightarrow{DB'}+\overrightarrow{BD}=\overrightarrow{BB'}\)
\(=\overrightarrow{DB'}+\overrightarrow{BD}=\overrightarrow{BB'}\)
c)  \(\overrightarrow{AC}+\overrightarrow{BA'}+\overrightarrow{DB}+\overrightarrow{C'D}\)
\(\overrightarrow{AC}+\overrightarrow{BA'}+\overrightarrow{DB}+\overrightarrow{C'D}\)
 \(=\overrightarrow{AC}+\left(\overrightarrow{C'D}+\overrightarrow{DB}+\overrightarrow{BA'}\right)\)
\(=\overrightarrow{AC}+\left(\overrightarrow{C'D}+\overrightarrow{DB}+\overrightarrow{BA'}\right)\)
 \(=\overrightarrow{A'C'}+\overrightarrow{C'A'}=\overrightarrow{0\ }\)
\(=\overrightarrow{A'C'}+\overrightarrow{C'A'}=\overrightarrow{0\ }\)
Cho hình bình hành ABCD. Gọi S là một điểm không thuộc mặt phẳng chứa hình bình hành. Chứng minh rằng ![]() \(\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}\).
\(\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}\).
Gợi ý đáp án
Do ABCD là hình bình hành nên ![]() \(\overrightarrow{AD}=\overrightarrow{BC}\)
\(\overrightarrow{AD}=\overrightarrow{BC}\)
Suy ra ![]() \(\overrightarrow{SD}-\overrightarrow{SA}=\overrightarrow{SC}-\overrightarrow{SB}\)
\(\overrightarrow{SD}-\overrightarrow{SA}=\overrightarrow{SC}-\overrightarrow{SB}\)
Do đó ![]() \(\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}\).
\(\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}\).
Ba lực có điểm đặt tại một đỉnh của hình lập phương, cùng phương với ba cạnh và cùng có cường độ là 5 N. Tính cường độ của hợp lực.
Gợi ý đáp án
Giả sử ba lực đó là  \(\overrightarrow{AB};\ \overrightarrow{AD};\ \overrightarrow{AA'}\) của hình lập phương ABCD.A'B'C'D'.
\(\overrightarrow{AB};\ \overrightarrow{AD};\ \overrightarrow{AA'}\) của hình lập phương ABCD.A'B'C'D'.
Áp dụng quy tắc hình hộp, ta có:
 \(\overrightarrow{AB}+\ \overrightarrow{AD}+\ \overrightarrow{AA'}=\overrightarrow{AC'}\)
\(\overrightarrow{AB}+\ \overrightarrow{AD}+\ \overrightarrow{AA'}=\overrightarrow{AC'}\)
Khi đó, cường độ của hợp lực là:
 \(\left|\overrightarrow{AC'}\right|=\sqrt{AA'^2+A'C'^2}=\sqrt{5^2+\left(5\sqrt{2}\right)^2}=5\sqrt{3}\) (N).
\(\left|\overrightarrow{AC'}\right|=\sqrt{AA'^2+A'C'^2}=\sqrt{5^2+\left(5\sqrt{2}\right)^2}=5\sqrt{3}\) (N).
Cho hình chóp S.ABCD. Gọi I là trọng tâm của tam giác ABC và J là trọng tâm tam giác ADC. Chứng minh rằng ![]() \(2\overrightarrow{SA}+\overrightarrow{SB}+2\overrightarrow{SC}+\overrightarrow{SD}=3(\overrightarrow{SI}+\overrightarrow{SJ})\).
\(2\overrightarrow{SA}+\overrightarrow{SB}+2\overrightarrow{SC}+\overrightarrow{SD}=3(\overrightarrow{SI}+\overrightarrow{SJ})\).
Gợi ý đáp án
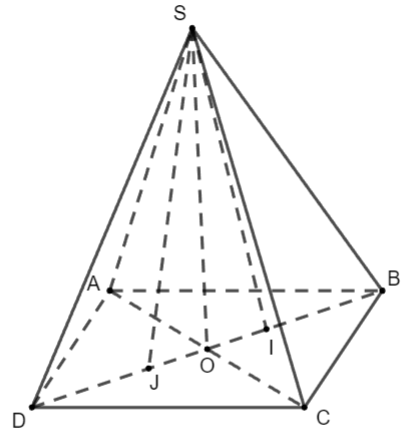
Do I, J lần lượt là trọng tâm tam giác ABC và ADC
Suy ra ![]() \(\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=3\overrightarrow{SI}\) (1)
\(\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}=3\overrightarrow{SI}\) (1)
![]() \(\overrightarrow{SA}+\overrightarrow{SD}+\overrightarrow{SC}=3\overrightarrow{SJ}\) (2)
\(\overrightarrow{SA}+\overrightarrow{SD}+\overrightarrow{SC}=3\overrightarrow{SJ}\) (2)
Cộng vế với vế của (1) và (2), ta có:
![]() \(2\overrightarrow{SA}+\overrightarrow{SB}+2\overrightarrow{SC}+\overrightarrow{SD}=3(\overrightarrow{SI}+\overrightarrow{SJ})\) (đpcm)
\(2\overrightarrow{SA}+\overrightarrow{SB}+2\overrightarrow{SC}+\overrightarrow{SD}=3(\overrightarrow{SI}+\overrightarrow{SJ})\) (đpcm)
Cho hình lăng trụ tam giác ABC.A'B'C' có  \(\overrightarrow{AA'}=\overrightarrow{a},\overrightarrow{AB}=\overrightarrow{b},\overrightarrow{AC}=\overrightarrow{c\ }\). Chứng minh rằng
\(\overrightarrow{AA'}=\overrightarrow{a},\overrightarrow{AB}=\overrightarrow{b},\overrightarrow{AC}=\overrightarrow{c\ }\). Chứng minh rằng  \(\overrightarrow{B'C}=\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b\ }\) và
\(\overrightarrow{B'C}=\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b\ }\) và  \(\overrightarrow{BC'}=\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c\ }\)
\(\overrightarrow{BC'}=\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c\ }\)
Gợi ý đáp án
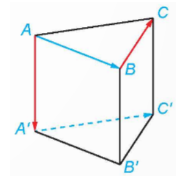
Ta có:  \(\overrightarrow{B'C}=\overrightarrow{AC}-\overrightarrow{AB'}\)
\(\overrightarrow{B'C}=\overrightarrow{AC}-\overrightarrow{AB'}\)
 \(=\overrightarrow{AC}-\left(\overrightarrow{AB}+\overrightarrow{AA'}\right)\)
\(=\overrightarrow{AC}-\left(\overrightarrow{AB}+\overrightarrow{AA'}\right)\)
![]() \(=\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b\ }\)
\(=\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b\ }\)
Ta có:  \(\overrightarrow{BC'}=\overrightarrow{AC'}-\overrightarrow{AB}\)
\(\overrightarrow{BC'}=\overrightarrow{AC'}-\overrightarrow{AB}\)
 \(=\overrightarrow{AA'}+\overrightarrow{AC}-\overrightarrow{AB}\)
\(=\overrightarrow{AA'}+\overrightarrow{AC}-\overrightarrow{AB}\)
 \(=\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{AC}\)
\(=\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{AC}\)
![]() \(=\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c\ }\)
\(=\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c\ }\)
Nếu một vật có khối lượng m (kg) thì lực hấp dẫn ![]() \(\overrightarrow{P\ }\) của Trái Đất tác dụng lên vật được xác định theo công thức
\(\overrightarrow{P\ }\) của Trái Đất tác dụng lên vật được xác định theo công thức ![]() \(\overrightarrow{P}=m\overrightarrow{g\ }\), trong đó
\(\overrightarrow{P}=m\overrightarrow{g\ }\), trong đó ![]() \(\overrightarrow g\) là gia tốc rơi tự do có độ lớn 9,8 m/s2. Tính độ lớn của lực hấp dẫn của Trái Đất tác dụng lên một quả táo có khối lượng 102 gam (Hình 28).
\(\overrightarrow g\) là gia tốc rơi tự do có độ lớn 9,8 m/s2. Tính độ lớn của lực hấp dẫn của Trái Đất tác dụng lên một quả táo có khối lượng 102 gam (Hình 28).
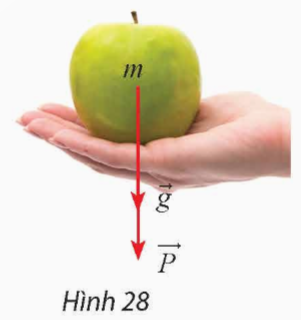
Gợi ý đáp án
m = 102 g = 0,102
Độ lớn của lực hấp dẫn là:
P = m . g = 0,102 . 9,8 = 0,9996 (N)
Trong điện trường đều, lực tĩnh điện ![]() \(\overrightarrow{F\ }\) (đơn vị: N) tác dụng lên điện tích điểm có điện tích q (đơn vị: C) được tính theo công thức
\(\overrightarrow{F\ }\) (đơn vị: N) tác dụng lên điện tích điểm có điện tích q (đơn vị: C) được tính theo công thức ![]() \(\overrightarrow{F}=q.\overrightarrow{E\ }\), trong đó
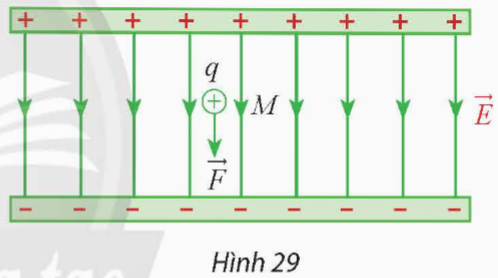
\(\overrightarrow{F}=q.\overrightarrow{E\ }\), trong đó ![]() \(\overrightarrow{E\ }\) là cường độ điện trường (đơn vị: N/C). Tính độ lớn của lực tĩnh điện tác dụng lên điện tích điểm khi q = 10- 9 C và độ lớn điện trường E = 105 N/C (Hình 29).
\(\overrightarrow{E\ }\) là cường độ điện trường (đơn vị: N/C). Tính độ lớn của lực tĩnh điện tác dụng lên điện tích điểm khi q = 10- 9 C và độ lớn điện trường E = 105 N/C (Hình 29).
Gợi ý đáp án
Độ lớn của lực tĩnh điện tác đụng lên điện tích điểm là:
F = q . E = 10- 9 . 105 = 0,0001 (N)
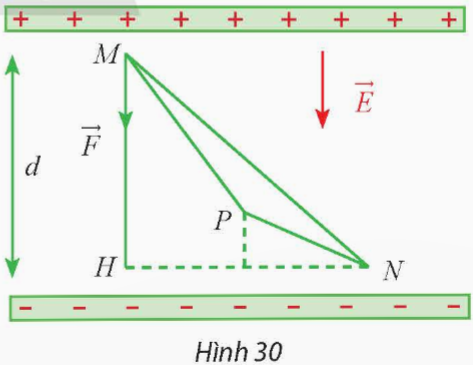
Một lực tĩnh điện ![]() \(\overrightarrow{F\ }\) tác động lên điện tích điểm M trong điện trường đều làm cho M dịch chuyển theo đường gấp khúc MPN (Hình 30). Biết q = 2 . 10- 12 C, vectơ điện trường có độ lớn E = 1,8 . 105 N/C và d = MH = 5 mm. Tính công A sinh bởi lực tĩnh điện
\(\overrightarrow{F\ }\) tác động lên điện tích điểm M trong điện trường đều làm cho M dịch chuyển theo đường gấp khúc MPN (Hình 30). Biết q = 2 . 10- 12 C, vectơ điện trường có độ lớn E = 1,8 . 105 N/C và d = MH = 5 mm. Tính công A sinh bởi lực tĩnh điện ![]() \(\overrightarrow{F\ }\).
\(\overrightarrow{F\ }\).
Gợi ý đáp án
Công A sinh ra bởi lực tĩnh điện ![]() \(\overrightarrow{F\ }\) là:
\(\overrightarrow{F\ }\) là:
A = q . E . d = 2 . 10- 12 . 1,8 . 105 . 0,005
= 1,8 . 10- 9 (J)
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: