Toán 12 Bài 7: Hệ trục tọa độ trong không gian Giải Toán 12 Kết nối tri thức trang 60 → 66

Giải Toán 12 Bài 7: Hệ trục tọa độ trong không gian là tài liệu vô cùng hữu ích giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 12 Kết nối tri thức với cuộc sống tập 1 trang 60, 61, 62, 63, 64, 65, 66.

Giải bài tập Toán 12 Kết nối tri thức tập 1 Bài 7 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 7 Chương II: Vectơ và hệ trục tọa độ trong không gian. Mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Giải Toán 12 Kết nối tri thức Tập 1 trang 64, 65

Bài 2.13

Trong không gian Oxyz, cho ba vectơ \(\vec{a}, \vec{b} , \vec{c}\) đều khác \(\vec{0}\) và có giá đôi một vuông góc. Những mệnh đề nào sau đây là đúng?

a) Có thể lập một hệ tọa độ Oxyz có các trục tọa độ lần lượt song song với giá của các vectơ \(\vec{a}, \vec{b} , \vec{c}\).

b) Có thể lập một hệ tọa độ Oxyz có các trục tọa độ lần lượt trùng với giá của các vectơ \(\vec{a}, \vec{b} , \vec{c}\).

c) Có thể lập một hệ tọa độ Oxyz có các vectơ \(\vec{i} , \vec{j} , \vec{k}\) lần lượt bằng các vectơ \(\vec{a}, \vec{b} , \vec{c}\) .

d) Có thể lập một hệ tọa độ Oxyz có các vectơ \(\vec{i} , \vec{j} , \vec{k}\) lần lượt cùng phương với các vectơ \(\vec{a}, \vec{b} , \vec{c}\)

Hướng dẫn giải:

Các mệnh đề đúng là: a, d

Bài 2.14

Hãy mô tả hệ tọa độ Oxyz trong căn phòng ở Hình 2.44 sao cho gốc O trùng với góc trên của căn phòng, khung tranh nằm trong mặt phẳng (Oxy) và mặt trần nhà trùng với mặt phẳng (Oxz).

Hướng dẫn giải:

Trục Ox là mép trần nhà nằm trên bức tường chứa bức tranh, trục Oy là mép còn lại của bức tường chưa bức tranh, trục Oz là mép trần nhà còn lại.

Bài 2.15

Trong không gian Oxyz, xác định tọa độ của vectơ \(\vec{AB}\) trong mỗi trường hợp sau:

a) A(0; 0; 0) và B(4; 2; − 5)

b) A(1; − 3; 7) và B(1; − 3; 7)

c) A(5; 4; 9) và B(− 5; 7; 2)

Hướng dẫn giải:

a) \(\overrightarrow{AB}=(4;2;-5)\)

b) \(\overrightarrow{AB}=(0;0;0)\)

c) \(\overrightarrow{AB}=(-10;3;-7)\)

Bài 2.16

Trong không gian Oxyz, xác định tọa độ của điểm A trong mỗi trường hợp sau:

a) A trùng với gốc tọa độ

b) A nằm trên tia Ox và OA = 2

c) A nằm trên tia đối của tia Oy và OA = 3

Hướng dẫn giải:

a) A(0; 0; 0)

b) A(2; 0; 0)

c) A(0; - 3; 0)

Bài 2.17

Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A'B'C'D' có đỉnh A trùng với gốc O và các đỉnh D, B, A' có tọa độ lần lượt là (2; 0; 0), (0; 4; 0), (0; 0; 3) (H.2.45). Xác định tọa độ của các đỉnh còn lại của hình hộp chữ nhật.

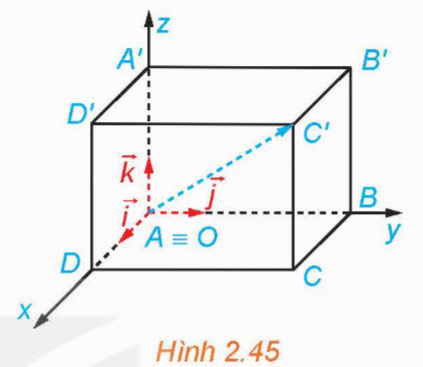
Hướng dẫn giải:

A(0; 0; 0); C(2; 4; 0)

B'(0; 4; 3); C'(2; 4; 3)

D'(2; 0; 3)

Bài 2.18

Trong không gian Oxyz, cho hình hộp OABC.O'A'B'C' có A(1; 1; − 1), B(0; 3; 0), C'(2; − 3; 6).

a) Xác định tọa độ của điểm C.

b) Xác định tọa độ các đỉnh còn lại của hình hộp.

Hướng dẫn giải:

Giả sử tọa độ của C là (x; y; z) và tọa độ của O' là (a; b; c)

Ta có: \(\overrightarrow{OC}=(x;y;z)\)

\(\overrightarrow{AB}=(- 1; 2; 1)\)

Để OABC.O'A'B'C' là hình hộp thì:

• \(\overrightarrow{OC}=\overrightarrow{AB}\)

Do đó x = - 1; y = 2 và z = 1. Vậy C(- 1; 2; 1)

Ta có: \(\overrightarrow{OO'}=(a;b;c)\); \(\overrightarrow{CC'}=(3;-5;-5)\)

• \(\overrightarrow{OO'}=\overrightarrow{CC'}\)

Do đó x = 3; y = - 5 và z = - 5. Vậy O'(3; - 5; - 5)

Bài 2.19

Trong Vận dụng 2, hãy giải thích vì sao tại mỗi thời điểm chiếc máy bay di chuyển trên đường băng thì tọa độ của nó luôn có dạng (x; y; 0) với x, y là hai số thực nào đó.