Toán 12 Bài tập cuối chương I Giải Toán 12 Chân trời sáng tạo trang 37, 38, 39

Giải Toán 12 Bài tập cuối chương I là tài liệu vô cùng hữu ích giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 37, 38, 39.

Giải bài tập Toán 12 Chân trời sáng tạo tập 1 Bài tập cuối chương I được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài tập cuối chương I: Ứng dụng đạo hàm để khảo sát hàm số. Mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Giải Toán 12 Chân trời sáng tạo Tập 1 trang 37, 38 - Trắc nghiệm

Bài 1

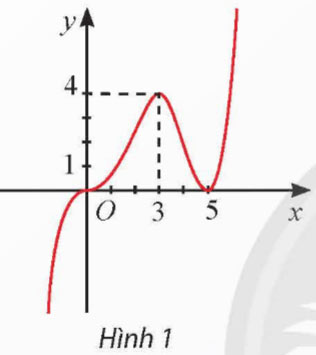
Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số y = f(x) đồng biến trên khoảng

A. (5; + ∞). B. (3; 5). C. (0; 5). D. (3; + ∞).

Đáp án đúng: A

Bài 2

Cho hàm số y = f(x) có đồ thị như Hình 1. Hàm số đạt cực đại tại

A. x = 0. B. x = 3. C. x = 4. D. x = 5.

Đáp án đúng: B

Bài 3

Cho hàm số \(y = \frac{x^{2}-4x+1 }{x-4}\). Trong các khẳng định sau, khẳng định nào đúng?

A. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 2.

B. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 6.

C. Hàm số đạt cực tiểu tại x = 3, giá trị cực tiểu là y = 6.

D. Hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là y = 2.

Đáp án đúng: B

Bài 4

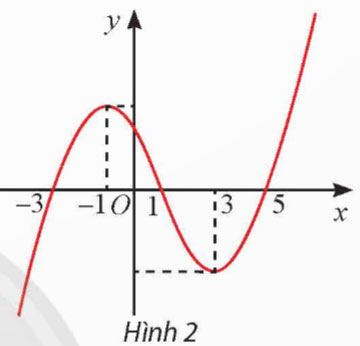
Đạo hàm của hàm số y = f(x) là hàm số có đồ thị được cho trong Hình 2. Hàm số y = f(x) nghịch biến trên khoảng

A. (– 1; 3). B. (– 3; 1). C. (1; 5). D. (3; + ∞).

Đáp án đúng: C

Bài 5

Giá trị nhỏ nhất của hàm số \(y = \sqrt {{x^2} + 2x + 3}\) trên đoạn [–2; 3] là

A. \(\sqrt 3\)

B. \(\sqrt {30}\)

C. \(\sqrt 2\)

D. 0

Đáp án đúng: C

Bài 6

Tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^3} + 3{x^2} - 3}}{{{x^2} - 1}}\) là đường thẳng có phương trình:

Đáp án đúng: A

Bài 7

Tiệm cận đứng của đồ thị hàm số \(y = \frac{{ - 2x + 3}}{{5x + 1}}\) là đường thẳng có phương trình

Đáp án đúng: B

Bài 8

Cho hàm \(y = \frac{{ - 2x - 3}}{{4 - x}}\). Trong các khẳng định sau, khẳng định nào đúng?

A. Hàm số đồng biến trên \(( - \infty ; –4)\) và nghịch biến trên \((–4; + \infty )\).

B. Hàm số đồng biến trên \(( - \infty ; 4)\) và \((4; + \infty )\).

C. Hàm số nghịch biến trên \(( - \infty ; 4)\) và \((4; + \infty )\).

D. Hàm số nghịch biến trên \((- \infty ; –4)\) và \((–4; + \infty )\).

Đáp án đúng: C

Giải Toán 12 Chân trời sáng tạo Tập 1 trang 38, 39 - Tự luận

Bài 9

Tìm hai số không âm a và b có tổng bằng 10 sao cho:

a) Biểu thức ab đạt giá trị lớn nhất;

b) Tổng bình phương của chúng đạt giá trị nhỏ nhất;

c) Biểu thức ab² đạt giá trị lớn nhất

Hướng dẫn giải:

Ta có hai số đó là: a và b = 10 - a (0 ≤ a ≤10)

a) Xét hàm số M(a) = ab = 10a - a²

Ta có M'(a) = 10 - 2a; M'(a) = 0 ⇔ a = 5

M(0) = 0; M(5) = 25; M(10) = 0

Do đó, \(\underset{[0;10]}{\max} M(a) = M(5)=25\)

Vậy biểu thức ab đạt giá trị lớn nhất khi a = b = 5.

b) Xét hàm số N(a) = a² + b²

= 2a² - 20a + 100

Ta có N'(a) = 4a - 20; N'(a) = 0 ⇔ a = 5

N(0) = 100; N(5) = 50; N(10) = 100

Do đó, \(\underset{[0;10]}{\min} N(a) = N(0)=N(10)=100\)

Vậy a = b = 5 thì N(a) đạt giá trị nhỏ nhất.

c) Xét hàm số P(a) = ab²

= a³ - 20a² + 100a

Ta có P'(a) = 3a² - 40a + 100;

P'(a) = 0 ⇔ \(a=\frac{10}{3}\) hoặc a = 10.

P(0) = 0; \(P\left(\frac{10}{3}\right)=\frac{4000}{27}\); P(10) = 0

Do đó, \(\underset{[0;10]}{\max} P(a) =P\left(\frac{10}{3}\right)=\frac{4000}{27}\)

Vậy \(a=\frac{10}{3};\ b=\frac{20}{3}\) thì P(a) đạt giá trị lớn nhất.

Bài 10

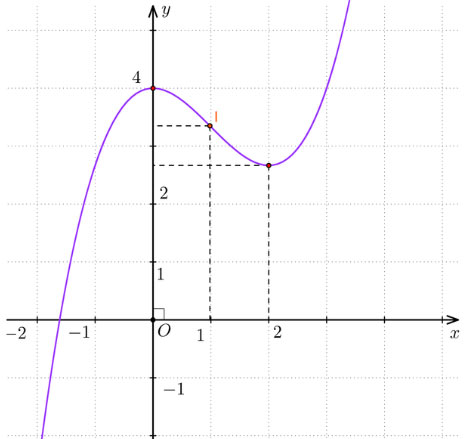
Cho hàm số bậc ba y = f(x) có đồ thị như Hình 3. Viết công thức của hàm số.

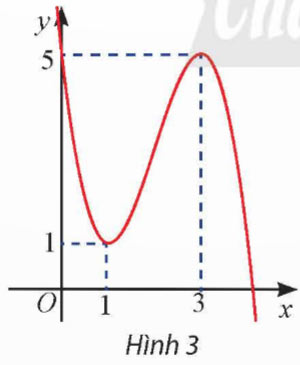
Hướng dẫn giải:

Giả sử hàm số có dạng y = f(x) = ax³ + bx² + cx + d.

Ta có: y' = 3ax² + 2bx + c

Từ đồ thị ta có:

\(\left\{\begin{array}{1} f(0)=5 \\ f(1)=1 \\ f(3)=5 \\ f'(1)=0 \\ f'(3)=0 \end{array} \right. \Leftrightarrow \left\{ \begin{array} {1} d = 5 \\ a + b + c + d = 1 \\ 27a + 9b + 3c + d = 5 \\ 27a + 6b + c = 0 \\ 3a + 2b +c =0 \end{array} \right.\)

\(\Leftrightarrow \left\{\begin{array}{1} a=-1 \\ b=6 \\ c = - 9\\ d = 5 \end{array} \right.\)

Vậy công thức hàm số là y = f(x) = - x³ + 6x² - 9x + 5

Bài 11

Cho hàm số \(y = \frac{1}{3}{x^3} - {x^2} + 4\).

a) Khảo sát và vẽ đồ thị của hàm số.

b) Tính khoảng cách giữa hai điểm cực trị của đồ thị hàm số.

Hướng dẫn giải:

a) Xét hàm số \(y = \frac{1}{3}{x^3} - {x^2} + 4\)

1. Tập xác định: \(\mathbb{R}\).

2. Sự biến thiên:

• Chiều biến thiên:

Đạo hàm y' = x² - 2x. Ta có: y' = 0 ⇔ x = 0 hoặc x = 2

Trên các khoảng \((– ∞; 0)\) và \((2; +\infty )\), y' > 0 nên hàm số đồng biến trên từng khoảng đó.

Trên khoảng (0; 2), y' < 0 nên hàm số nghịch biến trên khoảng đó.

• Cực trị:

Hàm số đạt cực đại tại x = 0 và y_CĐ = 4.

Hàm số đạt cực tiểu tại x = 2 và y_CT = \(\frac{8}{3}\).

• Các giới hạn tại vô cực:

\(\lim_{x \rightarrow -\infty} y=\lim_{x \rightarrow -\infty}x^3 \left ( \frac{1}{3}-\frac{1}{x }+\frac{ 4}{x^3} \right ) =-∞\)

\(\lim_{x \rightarrow +\infty} y=\lim_{x \rightarrow -\infty}x^3 \left ( \frac{1}{3}-\frac{1}{x }+\frac{ 4}{x^3} \right ) =+∞\)

• Bảng biến thiên:

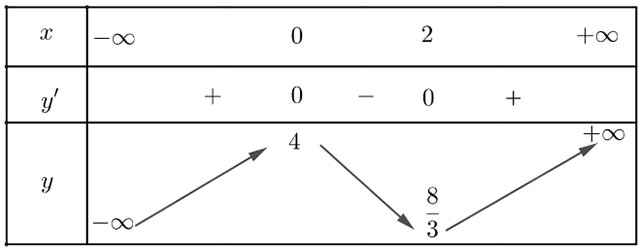
3. Đồ thị

Khi x = 0 thì y = 4 nên (0; 4) là giao điểm của đồ thị với trục Oy.

Ta có y = 0 ⇔ \(\frac{1}{3}{x^3} - {x^2} + 4 =0\)

⇔ x = - 1,612

Vậy đồ thị của hàm số giao với trục Ox tại điểm (- 1,612; 0).

Điểm (0; 4) là điểm cực đại và điểm (2; \(\frac{8}{3}\)) là điểm cực tiểu của đồ thị hàm số.

Đồ thị của hàm số có tâm đối xứng là điểm \(I\left(1;\frac{10}{3}\right)\)

b) Khoảng cách giữa hai điểm cực trị là: \(\frac{2\sqrt{13}}{3}\).

Bài 12

Cho hàm số \(y = \frac{{2x + 1}}{{x - 1}}\)

a) Khảo sát và vẽ đồ thị của hàm số.

b) Gọi A là giao điểm của đồ thị hàm số với trục Oy, I là giao điểm của hai đường tiệm cận của đồ thị hàm số. Tìm điểm B đối xứng với A qua I. Chứng minh rằng điểm B cũng thuộc đồ thị hàm số này.

Hướng dẫn giải:

a) Xét hàm số \(y = \frac{{2x + 1}}{{x - 1}}\)

1. Tập xác định: \(D=\mathbb{R} \setminus \left \{ 1 \right \}\)

2. Sự biến thiên:

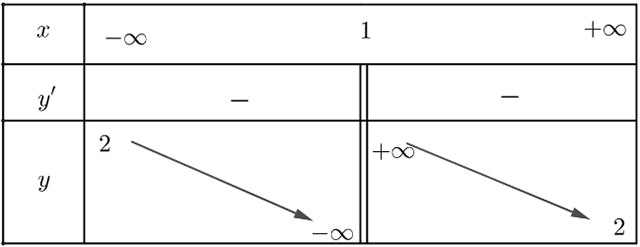
• Chiều biến thiên:

Đạo hàm \(y'=-\frac{3}{\left(x-1\right)^2}\). Vì y' < 0 nên hàm số nghịch biến trên mỗi khoảng \((– ∞; 1)\) và \((1; + ∞)\).

• Tiệm cận:

Ta có: \(\lim_{x \rightarrow +\infty} y = \lim_{x \rightarrow +\infty} \frac{{2x + 1}}{{x - 1}} =2;\) \(\lim_{x \rightarrow -\infty} y = \lim_{x \rightarrow -\infty} \frac{{2x + 1}}{{x - 1}} = 2\). Suy ra đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.

Ta có: \(\lim_{x \rightarrow 1^+} y = \lim_{x \rightarrow 1^+} \frac{{2x + 1}}{{x - 1}} =+\infty ;\) \(\lim_{x \rightarrow 1^-} y = \lim_{x \rightarrow 1^-} \frac{{2x + 1}}{{x - 1}} =-\infty\). Suy ra đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.

• Bảng biến thiên:

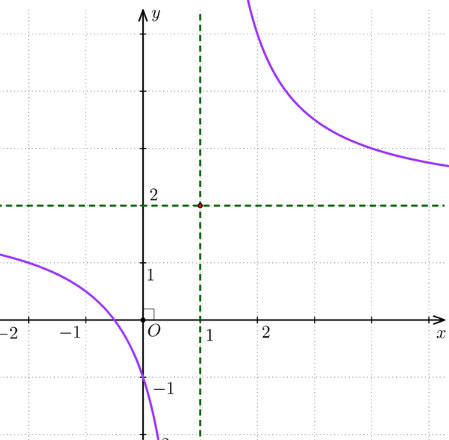
3. Đồ thị

Khi x = 0 thì y = - 1 nên A (0; - 1) là giao điểm của đồ thị với trục Oy.

Ta có y = 0 ⇔ \(\frac{2x+1}{x-1}=0\)

⇔ \(x=-\frac{1}{2}\)

Vậy đồ thị của hàm số giao với trục Ox tại điểm \(\left(-\frac{1}{2};0\right)\).

Tâm đối xứng của đồ thị hàm số là điểm I(1; 2).

Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận x = 1 và y = 2.

b) B thuộc đồ thị hàm số nên \(B\left(x;\frac{2x+1}{x-1}\right)\)

Ta có B đối xứng với A qua I nên I là trung điểm của AB.

Do đó: \(\left\{\begin{array}{1} x_I=\frac{x_A+x_B}{2} \\ y_I=\frac{y_A+y_B}{2} \end{array}\right. \Leftrightarrow \left\{\begin{array}{1} x_B=2x_I - x_A \\ y_B=2y_I - y_A \end{array}\right.\)

\(\Leftrightarrow \left\{\begin{array}{1} x =2.1-0 \\ \frac{2x+1}{x-1} =2.2-(-1) \end{array}\right. \Leftrightarrow x= 2\)

Vậy tọa độ điểm B là (2; 5).

Bài 13

Cho hàm số \(y = \frac{{{x^2} + 4x - 1}}{{x - 1}}\)

a) Khảo sát và vẽ đồ thị của hàm số.

b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [2; 4].

Bài 14

Cho một hình trụ nội tiếp trong hình nón có chiều cao bằng 12 cm và bán kính đáy bằng 5 cm (Hình 4a). Người ta cắt hình nón, trụ này theo mặt phẳng chứa đường thẳng nối đỉnh và tâm hình tròn đáy của hình nón thì thu được một hình phẳng như Hình 4b.

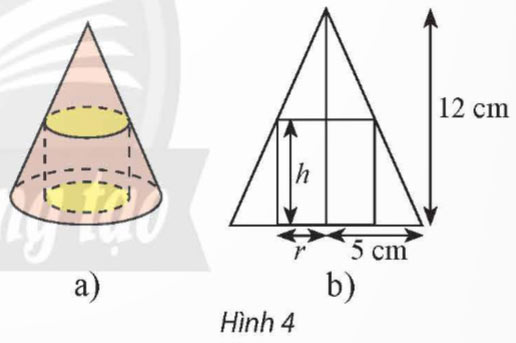
a) Chứng minh rằng công thức tính bán kính r của đáy hình trụ theo chiều cao h của nó là: \(r = \frac{{5(12 - h)}}{{12}}\)

b) Chứng minh biểu thức sau biểu thị thể tích khối trụ theo h: \(V(h) = \frac{{25\pi h{{(12 - h)}^2}}}{{144}}\)

c) Tìm h để khối trụ có thể tích lớn nhất.

Bài 15

Trong một nhà hàng, mỗi tuần để chế biến x phần ăn (x lấy giá trị trong khoảng từ 30 đến 120) thì chi phí trung bình (đơn vị: nghìn đồng) của một phần ăn được cho bởi công thức:

\(\overline C (x) = 2x - 230 + \frac{{7200}}{x}\)

a) Khảo sát và vẽ đồ thị hàm số \(\overline C (x)\) trên [30; 120].

b) Từ kết quả trên, tìm số phần ăn sao cho chi phí trung bình của một phần ăn là thấp nhất.