Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Một số bài toán phương trình logarit khác cơ số Tài liệu ôn tập môn Toán lớp 12
Mua gói Pro để tải file trên Download.vn và trải nghiệm website không quảng cáo
Tìm hiểu thêm »Nhằm đem đến cho các bạn học sinh lớp 12 có thêm nhiều tài liệu học tập môn Toán Download.vn xin giới thiệu tài liệu Một số bài toán phương trình logarit khác cơ số.
Để giải các dạng bài tập về phương trình logarit với cơ số khác nhau, nhiều học sinh thường lúng túng khi biến đổi, gặp khó khăn để đưa về cùng cơ số hoặc đưa về các phương trình cơ bản.Tài liệu này sẽ giới thiệu các phương pháp thường được áp dụng để giải dạng toán này. Bao gồm: Đổi cơ số; Đặt ẩn phụ để đưa về phương trình mũ; Biến đổi tương đương; Đánh giá hai vế. Hy vọng qua tài liệu này các bạn nắm vững được kiến thức giải nhanh các bài toán để đạt kết quả cao trong các bài kiểm tra, bài thi THPT Quốc gia. Mời các bạn cùng theo dõi.
Một số bài toán phương trình logarit khác cơ số
Chuaån bò cho kyø thi Ñaïi hoïc
Page 1
V
VV
Vài bài toán về phương trình
logarit khác cơ số
Huỳnh Đức Khánh – 0975.120.189
Descartes Giải tích – ĐH Quy Nhơn
P
hương trình logarit với cơ số khác nhau luôn là vấn đề gây khó dễ cho học sinh khi gặp phải
trong các đề thi. Học sinh thường lúng túng khi biến đổi, gặp khó khăn để đưa về cùng cơ số hoặc đưa về
các phương trình cơ bản. Tôi viết bài xin đóng góp vài bài mẫu về vấn đề này, nó được dùng các phương
pháp: Đổi cơ số, đặt ẩn phụ để đưa về phương trình mũ, biến đổi tương đương, đánh giá hai vế.
Ví dụ 1. Giải phương trình:
2 3 4 20
log x log x log x log x+ + = .
Điều kiện:
x 0>
.
Với điều kiện trên phương trình tương đương
2 3 2 4 2 20 2
log x log 2.log x log 2.log x log 2.log x+ + =
(
)
2 3 4 20
log x 1 log 2 log 2 log 2 0⇔ + + − =
2
log x 0⇔ =
(do
3 4 20
1 log 2 log 2 log 2 0+ + − ≠
)
x 1⇔ =
(thỏa mãn).
Vậy phương trình có nghiệm
x 1=
.
Ví dụ 2. Giải phương trình:
(
)
2
3 2
log x 3x 13 log x− − =
.
Điều kiện:
2
x 3x 13 0
3 61
x
x 0
2
− − >
+
⇔ >
>
.
Đặt:
t
2
log x t x 2= ⇔ =
.
Phương trình trở thành:
( )
t t
3
log 4 3.2 13 t− − =
t t t
4 3.2 13 3⇔ − − =
t t t
3 1 2
1 13 3
4 4 4
⇔ = + +
. (*)
Hàm số
t t t
3 1 2
y 13 3
4 4 4
= + +
là tổng của các hàm nghịch biến nên y nghịch biến,
hàm
y 1=
là hàm hằng. Do đó phương trình (*) có nghiệm duy nhất.
Ta có:
3 3 3
3 1 2
1 13 3
4 4 4
= + +
. Suy ra phương trình (*) có nghiệm
t 3=
.
Với
3
t 3 x 2 8= ⇒ = =
(thỏa mãn).
Vậy phương trình có nghiệm duy nhất
x 8=
.
Chuaån bò cho kyø thi Ñaïi hoïc
Page 2
Ví dụ 3. Giải phương trình:
(
)
2 3
log 1 x log x+ = .
Điều kiện: x 0> .
Đặt:
t
3
log x t x 3= ⇔ = .
Phương trình trở thành:
( )
t
2
log 1 3 t+ =
t t
1 3 2⇔ + =
t
t
1 3
1
2 2
⇔ + =
. (*)
Hàm số
t
t
1 3
y
2 2
= +
là tổng của các hàm nghịch biến nên y nghịch biến, hàm
y 1=
là hàm hằng. Do đó phương trình (*) có nghiệm duy nhất.
Ta có:
2
2
1 3
1
2 2
+ =
. Suy ra phương trình (*) có nghiệm
t 2=
.
Với
2
t 2 x 3 9= ⇒ = =
(thỏa mãn).
Vậy phương trình có nghiệm duy nhất
x 9=
.
Ví dụ 4. Giải phương trình:
(
)
(
)
2 2
3 2
log x 2x 1 log x 2x+ + = +
. (1)
Điều kiện:
2
2
x 2x 1 0 x 2
x 0
x 2x 0
+ + > < −
⇔
>
+ >
.
Đặt:
2
u x 2x= +
. Phương trình (1) trở thành:
(
)
3 2
log u 1 log u+ =
. (2)
Xét phương trình (2). Ta đặt:
t
2
log u t u 2= ⇔ =
.
Phương trình (2) trở thành:
( )
t
3
log 2 1 t+ =
t t
2 1 3⇔ + =
t t
2 1
1
3 3
⇔ + =
. (3)
Hàm số
t t
2 1
y
3 3
= +
là tổng của các hàm nghịch biến nên y nghịch biến, hàm
y 1=
là hàm hằng. Do đó phương trình (3) có nghiệm duy nhất.
Ta có:
1 1
2 1
1
3 3
+ =
. Suy ra phương trình (3) có nghiệm
t 1=
.
Với
1 2
x 1 3
t 1 u 2 2 x 2x 2
x 1 3
= − −
= ⇒ = = ⇒ + = ⇔
= − +
(thỏa mãn).
Vậy phương trình có nghiệm
x 1 3; x 1 3= − − = − +
.
Chuaån bò cho kyø thi Ñaïi hoïc
Page 3
Ví dụ 5. Giải phương trình:
(
)
(
)
3 5
log x 1 log 3x 1 4+ + + =
.
Điều kiện:
x 1 0
1
x
3x 1 0
3
+ >
⇔ > −
+ >
.
Đặt:
(
)
t
3
log x 1 t x 1 3+ = ⇔ + = , suy ra:
t
3x 1 3.3 2+ = −
.
Phương trình trở thành:
( )
t
5
t log 3.3 2 4+ − =
( )
t
5
log 3.3 2 4 t⇔ − = −
t 4 t
3.3 2 5
−
⇔ − =
t
t
625
3.3 2
5
⇔ − =
t t
3.15 2.5 625⇔ − =
t t
1 1
3 625 2
15 3
⇔ = +
.
Hàm số
t t
1 1
y 625 2
15 3
= +
là tổng của các hàm nghịch biến nên y nghịch biến, hàm
y 3=
là hàm hằng. Do đó phương trình có nghiệm duy nhất.
Ta có:
2 2
1 1
3 625 2
15 3
= +
. Suy ra phương trình có nghiệm
t 2=
.
Với
2
t 2 x 1 3 x 8= ⇒ + = ⇔ =
(thỏa mãn).
Vậy phương trình có nghiệm duy nhất
x 8=
.
Cách khác: ● Kiểm tra
x 8=
là nghiệm của phương trình.
● Nếu
x 8>
thì
(
)
(
)
(
)
(
)
( ) ( )
3 3
3 5
5 5
log x 1 log 8 1 2
log x 1 log 3x 1 4
log 3x 1 log 3.8 1 2
+ > + =
⇒ + + + >
+ > + =
.
● Nếu
x 8<
thì
(
)
(
)
(
)
(
)
( ) ( )
3 3
3 5
5 5
log x 1 log 8 1 2
log x 1 log 3x 1 4
log 3x 1 log 3.8 1 2
+ < + =
⇒ + + + <
+ < + =
.
Vậy phương trình có nghiệm duy nhất
x 8=
.
Chia sẻ bởi:
Trịnh Thị Thanh
Trịnh Thị Thanh
Liên kết tải về
Một số bài toán phương trình logarit khác cơ số
186,2 KB
Tải về
Có thể bạn quan tâm
-
Bài thơ Phò giá về kinh - Tụng giá hoàn kinh sư, Trần Quang Khải
-
Soạn bài Vẻ đẹp bài ca dao "Đứng bên ni đồng, ngó bên tê đồng" - Chân trời sáng tạo 6
-
Văn mẫu lớp 8: Phân tích tác phẩm Ca Huế trên sông Hương
-
Đoạn văn tiếng Anh về việc tự học (3 Mẫu)
-
GDCD 9 Bài 2: Khoan dung - Giáo dục công dân lớp 9 Cánh diều trang 11, 12, 13, 14, 15
-
Bộ đề thi học kì 2 lớp 5 năm 2024 - 2025 theo Thông tư 27
-
KHTN Lớp 6 Bài 10: Không khí và bảo vệ môi trường không khí
-
Bộ đề thi học kì 2 môn Lịch sử - Địa lí 8 năm 2024 - 2025 sách Kết nối tri thức với cuộc sống
-
Bài thơ Chiều xuân - Chiều xuân của Anh Thơ
-
Viết một bức thư ngắn cho một người bạn nước ngoài để làm quen
Nhiều người đang xem
Xác thực tài khoản!
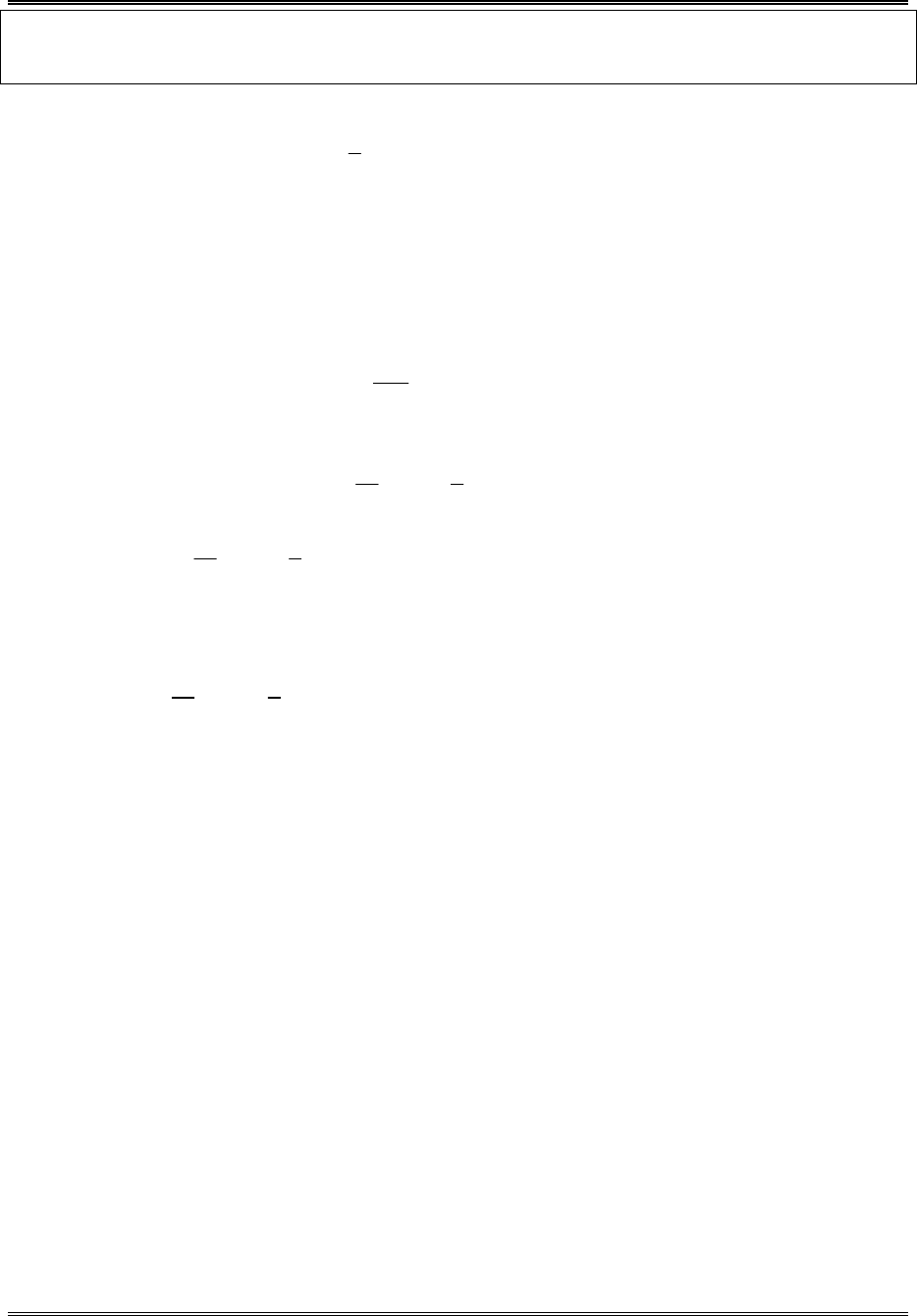
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
KHO TÀI LIỆU GIÁO DỤC & HỖ TRỢ CAO CẤP
Mở khóa quyền truy cập vào hàng ngàn tài liệu độc quyền và nhận hỗ trợ nhanh chóng từ đội ngũ của chúng tôi.
Mới nhất trong tuần
Đóng
Chỉ thành viên Download Pro tải được nội dung này!
Download Pro - Tải nhanh, website không quảng cáo!
Tìm hiểu thêm