Download.vn Học tập Lớp 12 Toán 12

Các dạng bài tập tính đơn điệu của hàm số Ôn tập môn Toán lớp 12

Tải về Bình luận
  • 24

Các dạng bài tập tính đơn điệu của hàm số là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 12 tham khảo.

Bài tập tính đơn điệu của hàm số gồm 59 trang tổng hợp các dạng bài tập trắc nghiệm thường xuất hiện trong các đề thi THPT Quốc gia qua các năm có đáp án kèm theo. Hi vọng qua tài liệu này giúp các bạn lớp 12 học tập chủ động, nâng cao kiến thức để đạt kết quả cao trong kì thi THPT Quốc gia sắp tới. Bên cạnh đó các bạn xem thêm: Bài tập phương trình phức, Bài tập thể tích khối chóp có một cạnh bên vuông góc với đáy, 572 câu trắc nghiệm chuyên đề Hàm số nâng cao.

Những nội dung trong tài liệu Tính đơn điệu của hàm số

PHẦN A. CÂU HỎI 

  • Dạng 1. Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị 
  • Dạng 2. Tìm khoảng đơn điệu của hàm số cho trước 
  • Dạng 3. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó 
  • Dạng 4. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước
  • Dạng 5. Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước 
  • Dạng 6. Tìm m để hàm số khác đơn điệu trên khoảng cho trước
  • Dạng 7. Tìm khoảng đơn điệu của hàm số f(u) khi biết đồ thị hàm số f’(x) 
  • Dạng 8. Tìm khoảng đơn điệu của hàm số f(u)+g(x) khi biết đồ thị, bảng biến thiên của hàm số f’(x) 12

PHẦN B. LỜI GIẢI THAM KHẢO

  • Dạng 1. Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị 
  • Dạng 2. Tìm khoảng đơn điệu của hàm số cho trước 
  • Dạng 3. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó 
  • Dạng 4. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước
  • Dạng 5. Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước 
  • Dạng 6. Tìm m để hàm số khác đơn điệu trên khoảng cho trước
  • Dạng 7. Tìm khoảng đơn điệu của hàm số f(u) khi biết đồ thị hàm số f’(x) 
  • Dạng 8. Tìm khoảng đơn điệu của hàm số f(u)+g(x) khi biết đồ thị, bảng biến thiên của hàm số f’(x) 52

Các dạng bài tập tính đơn điệu của hàm số

PHẦN A. CÂU HỎI

Dạng 1. Tìm khoảng đơn điệu của hàm số thông qua bảng biến thiên, đồ thị

Câu 1: (Mã 103 - BGD - 2019) Cho hàm số f(x)\(f(x)\) có bảng biến thiên như sau:

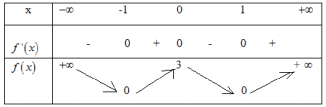
Hàm số đã cho đồng biến trên khoảng nào sau đây?

A. (-\infty;-1)\((-\infty;-1)\)                 B. (0;1)\((0;1)\)

C. (-1;0)\((-1;0)\)             D. (-1;+\infty)\((-1;+\infty)\)

Câu 2: (MĐ 104 BGD&DT NĂM 2017) Cho hàm số  y\ =\ f\ \left(x\right)\(y\ =\ f\ \left(x\right)\) có bảng xét dấu đạo hàm như sau

Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng(-\infty ;-2)\((-\infty ;-2)\)
B. Hàm số đồng biến trên khoảng (-2;0)\((-2;0)\)
C. Hàm số đồng biến trên khoảng (-\infty;0)\((-\infty;0)\)
D. Hàm số nghịch biến trên khoảng (0;2)\((0;2)\)

Câu 3: (Mã đề 101 BGD&ĐT NĂM 2018) Cho hàm số y\ =\ f\ \left(x\right)\(y\ =\ f\ \left(x\right)\) có bảng biến thiên như sau

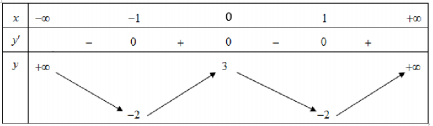
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. (-1;0)\((-1;0)\)              B. (-\infty ;0)\((-\infty ;0)\)

C. \left(1;+\infty\right)\(\left(1;+\infty\right)\)            D. \left(0;1\right)\(\left(0;1\right)\)

Câu 4: (Mã 102 - BGD - 2019) Cho hàm số f(x)\(f(x)\) có bảng biến thiên như sau:

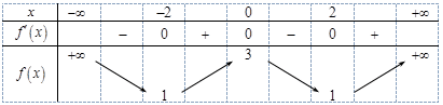
Hàm số đã cho đồng biến trên khoảng nào dưới đây 

A. (0;+\infty)\((0;+\infty)\)            B. \left(0;2\right)\(\left(0;2\right)\)

C. \left(-2;0\right)\(\left(-2;0\right)\)           D. \left(-\infty;-2\right)\(\left(-\infty;-2\right)\)

Câu 5: (MĐ 103 BGD&ĐT NĂM 2017-2018) Cho hàm số y\ =\ f\ \left(x\right)\(y\ =\ f\ \left(x\right)\) có bảng biến thiên như sau:

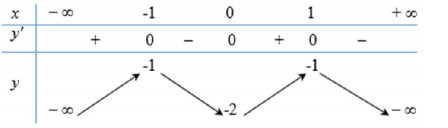
Hàm số đã cho đồng biến trên khoảng nào dưới đây? 

A. \left(0;1\right)\(\left(0;1\right)\)            B. (1;+\infty )\((1;+\infty )\)

C. \left(-\infty;1\right)\(\left(-\infty;1\right)\)         D. \left(-1;0\right)\(\left(-1;0\right)\)

Câu 6: (Mã đề 101 - BGD - 2019) Cho hàm số có bảng biến thiên như sau

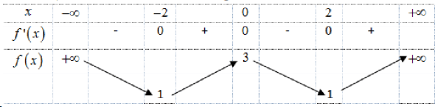
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. \left(0;2\right)\(\left(0;2\right)\)            B. \left(0;+\infty\right)\(\left(0;+\infty\right)\)

C. \left(-2;0\right)\(\left(-2;0\right)\)           D. \left(2;+\infty\right)\(\left(2;+\infty\right)\)

Câu 7: (Mã đề 102 BGD&ĐT NĂM 2018) Cho hàm số y\ =\ f\ \left(x\right)\(y\ =\ f\ \left(x\right)\) có bảng biến thiên như sau:

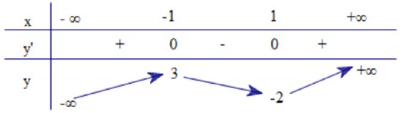
Hàm số đã cho đồng biến trên khoảng nào dưới đây? 

A.\left(-1;+\infty\right)\(\left(-1;+\infty\right)\)          B. \left(1;+\infty\right)\(\left(1;+\infty\right)\)

C. \left(-1;1\right)\(\left(-1;1\right)\)           D. \left(-\infty;1\right)\(\left(-\infty;1\right)\)

Câu 8: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Cho hàm số y\ =\ f\ \left(x\right)\(y\ =\ f\ \left(x\right)\) có đồ thị như hình vẽ dưới. 

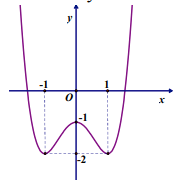
Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. \left(-\infty;-1\right)\(\left(-\infty;-1\right)\)           B. \left(-1;1\right)\(\left(-1;1\right)\)

C. \left(-1;0\right)\(\left(-1;0\right)\)            D. \left(0;1\right)\(\left(0;1\right)\)

Câu 9: (Mã đề 104 BGD&ĐT NĂM 2018) Cho hàm số y\ =\ f\ \left(x\right)\(y\ =\ f\ \left(x\right)\) có bảng biến thiên như sau

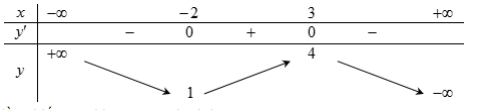
Hàm số đã cho đồng biến trên khoảng nào dưới đây? 

A. \left(-2;3\right)\(\left(-2;3\right)\)                B. \left(3;+\infty\right)\(\left(3;+\infty\right)\)

C. \left(-\infty;-2\right)\(\left(-\infty;-2\right)\)       D. \left(-2;+\infty\right)\(\left(-2;+\infty\right)\)

Câu 10: (ĐỀ THAM KHẢO BGD & ĐT 2018) Cho hàm số y\ =\ f\ \left(x\right)\(y\ =\ f\ \left(x\right)\) có bảng biến thiên như sau:

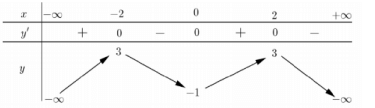
Hàm số trên nghịch biến trên khoảng nào dưới đây? 

A. \left(0;+\infty\right)\(\left(0;+\infty\right)\)            B. \left(-\infty;-2\right)\(\left(-\infty;-2\right)\)

C. \left(0;2\right)\(\left(0;2\right)\)              D. \left(-2;0\right)\(\left(-2;0\right)\)

Dạng 2. Tìm khoảng đơn điệu của hàm số cho trước

Câu 11: (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Hàm số nào dưới đây đồng biến trên khoảng \left(-\infty;+\infty\right)\(\left(-\infty;+\infty\right)\)?

A. y=\frac{x-1}{x-2}\(y=\frac{x-1}{x-2}\)         B. y=x^3+x\(y=x^3+x\)

C. y=-x^3-3x\(y=-x^3-3x\)       D. y=\frac{x+1}{x+3}\(y=\frac{x+1}{x+3}\)

Câu 12: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Cho hàm số  y=\frac{x-2}{x+1}\(y=\frac{x-2}{x+1}\). Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng \left(-\infty;+\infty\right)\(\left(-\infty;+\infty\right)\)
B. Hàm số nghịch biến trên khoảng \left(-1;+\infty\right)\(\left(-1;+\infty\right)\)
C. Hàm số nghịch biến trên khoảng \left(-\infty;-1\right)\(\left(-\infty;-1\right)\)
D. Hàm số đồng biến trên khoảng \left(-\infty;-1\right)\(\left(-\infty;-1\right)\)

Câu 13: (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Hàm số nào dưới đây đồng biến trên khoảng \left(-\infty;+\infty\right)\(\left(-\infty;+\infty\right)\)?

A. y=x^4+3x^2\(y=x^4+3x^2\)

B. y=\frac{x-2}{x+1}\(y=\frac{x-2}{x+1}\)

C. y=3x^3+3x-2\(y=3x^3+3x-2\)

D. y=2x^3-5x+1\(y=2x^3-5x+1\)

Câu 14: (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Cho hàm số y=x^3-3x^2\(y=x^3-3x^2\). Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng \left(0;2\right)\(\left(0;2\right)\)
B. Hàm số nghịch biến trên khoảng \left(0;2\right)\(\left(0;2\right)\)
C. Hàm số nghịch biến trên khoảng \left(-\infty;0\right)\(\left(-\infty;0\right)\)
D. Hàm số nghịch biến trên khoảng \left(2;+\infty\right)\(\left(2;+\infty\right)\)

Câu 15: (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Hỏi hàm số y=2x^4+1\(y=2x^4+1\) đồng biến trên khoảng nào?

A. \left(-\infty;0\right)\(\left(-\infty;0\right)\)        B. \left(-\infty;-\frac{1}{2}\right)\(\left(-\infty;-\frac{1}{2}\right)\)

C. \left(0;+\infty\right)\(\left(0;+\infty\right)\)         D. \left(-\frac{1}{2};+\infty\right)\(\left(-\frac{1}{2};+\infty\right)\)

Câu 16: (MĐ 105 BGD&ĐT NĂM 2017) Cho hàm số y=f\left(x\right)\(y=f\left(x\right)\) có đạo hàm f\(f'(x)=x^{2} +1, \forall x\in \mathbb{R}\). Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng \left(1;+\infty\right)\(\left(1;+\infty\right)\)
B. Hàm số nghịch biến trên khoảng \left(-1;1\right)\(\left(-1;1\right)\)
C. Hàm số đồng biến trên khoảng \left(-\infty;+\infty\right)\(\left(-\infty;+\infty\right)\)
D. Hàm số nghịch biến trên khoảng\left(-\infty;0\right)\(\left(-\infty;0\right)\)

Câu 17:Cho hàm số y=x^{3}-2 x^{2}+x+1\(y=x^{3}-2 x^{2}+x+1\). Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng (1 ;+\infty)\((1 ;+\infty)\)
B. Hàm số nghịch biến trên khoảng \left(\frac{1}{3} ; 1\right)\(\left(\frac{1}{3} ; 1\right)\)
C. Hàm số nghịch biến trên khoảng \left(-\infty ; \frac{1}{3}\right) \quad\(\left(-\infty ; \frac{1}{3}\right) \quad\)

D. Hàm số đồng biến trên khoảng \left(\frac{1}{3} ; 1\right)\(\left(\frac{1}{3} ; 1\right)\)

Câu 18: Cho hàm số y=x^{4}-2 x^{2}\(y=x^{4}-2 x^{2}\). Mệnh đề nào dưới đây đúng?

A. Hàm số nghịch biến trên khoảng (-\infty ;-2) \quad\((-\infty ;-2) \quad\)
B. Hàm số đồng biến trên khoảng (-1 ; 1)
C. Hàm số nghịch biến trên khoảng (-1 ; 1)
D. Hàm số đồng biến trên khoảng (-\infty ;-2)\((-\infty ;-2)\)

Câu 19: Hàm số y=\frac{2}{x^{2}+1}\(y=\frac{2}{x^{2}+1}\) nghịch biến trên khoảng nào dưới đây?

A. (-\infty ;+\infty)\((-\infty ;+\infty)\)
B. (0 ;+\infty)\((0 ;+\infty)\)
C. (-\infty ; 0)\((-\infty ; 0)\)
D. (-1 ; 1)

Câu 20: Cho hàm số y=x^{3}+3 x+2\(y=x^{3}+3 x+2\). Mệnh đề nào dưới đây là đúng?

A. Hàm số nghịch biến trên khoảng (-\infty ; 0)\((-\infty ; 0)\) và đồng biến trên khoảng (0 ;+\infty)\((0 ;+\infty)\)
B. Hàm số đồng biến trên khoảng (-\infty ; 0)\((-\infty ; 0)\) và đồng biến trên khoảng (0 ;+\infty)\((0 ;+\infty)\)
C. Hàm số đồng biến trên khoảng (-\infty ;+\infty)\((-\infty ;+\infty)\)
D. Hàm số nghịch biến trên khoảng (-\infty ;+\infty)\((-\infty ;+\infty)\) 

Câu 21: Cho hàm số y=\sqrt{2 x^{2}+1}\(y=\sqrt{2 x^{2}+1}\). Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng (0 ;+\infty)\((0 ;+\infty)\) 
B. Hàm số đồng biến trên khoảng (-\infty ; 0)\((-\infty ; 0)\)
C. Hàm số nghịch biến trên khoảng (0 ;+\infty)\((0 ;+\infty)\)
D. Hàm số nghịch biến trên khoảng (-1 ; 1)

Dạng 3. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó

Câu 22: Hỏi có bao nhiêu số nguyên m để hàm số y=\left(m^{2}-1\right) x^{3}+(m-1) x^{2}-x+4\(y=\left(m^{2}-1\right) x^{3}+(m-1) x^{2}-x+4\) nghịch biến trên khoảng (-\infty ;+\infty).\((-\infty ;+\infty).\)

A. 0
B. 3
C. 2
D. 1

Câu 23: Cho hàm số y=-x^{3}-m x^{2}+(4 m+9) x+5,\(y=-x^{3}-m x^{2}+(4 m+9) x+5,\) với m là tham số. Hỏi có bao nhiêu giá trị nguyên của \mathrm{m} để hàm số nghịch biến trên khoảng (-\infty ;+\infty)\((-\infty ;+\infty)\)

A. 5
B. 4
C. 6
D. 7

Câu 24:Hỏi có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số hàm số y=\frac{1}{3}\left(m^{2}-m\right) x^{3}+2 m x^{2}+3 x-2\(y=\frac{1}{3}\left(m^{2}-m\right) x^{3}+2 m x^{2}+3 x-2\) đồng biến trên khoảng (-\infty ;+\infty) ?\((-\infty ;+\infty) ?\)

A. 4 .
B. 5 .
C. 3 .
D. 0 .

Câu 25: Tìm tất cả các giá trị của tham số thực m để hàm số y=m x^{3}+m x^{2}+m(m-1) x+2\(y=m x^{3}+m x^{2}+m(m-1) x+2\) đồng biến trên R

A. m \leq \frac{4}{3} và m \neq 0.\(m \leq \frac{4}{3} và m \neq 0.\)
B. m=0 hoặc m \geq \frac{4}{3}.\(m \geq \frac{4}{3}.\)
C. m \geq \frac{4}{3}.\(m \geq \frac{4}{3}.\)
D. m \leq \frac{4}{3}.\(m \leq \frac{4}{3}.\)

Câu 26: Cho hàm số y=-\frac{1}{3} x^{3}+m x^{2}+(3 m+2) x+1\(y=-\frac{1}{3} x^{3}+m x^{2}+(3 m+2) x+1\). Tìm tất cả giá trị của m để hàm số nghịch biến trên R

A. \left[\begin{array}{l}m \geq-1 \\ m \leq-2\end{array}\right.\(A. \left[\begin{array}{l}m \geq-1 \\ m \leq-2\end{array}\right.\)

B. -2 \leq m \leq-1\(B. -2 \leq m \leq-1\)

C. -2<m<-1

D. \left[\begin{array}{l}m>-1 \\ m<-2\end{array}\right.\(D. \left[\begin{array}{l}m>-1 \\ m<-2\end{array}\right.\).

Câu 27: Tìm m để hàm số y=x^{3}-3 m x^{2}+3(2 m-1)+1\(y=x^{3}-3 m x^{2}+3(2 m-1)+1\) đồng biến trên R

A. Không có giá trị m thỏa mãn.

B. m \neq 1.\(m \neq 1.\)

C. m=1.

D. Luôn thỏa mãn với mọi m.

Câu 28: Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số y=\frac{m}{3} x^{3}-2 m x^{2}+(3 m+5) x\(y=\frac{m}{3} x^{3}-2 m x^{2}+(3 m+5) x\) đồng biến trên R

A. 4 .

B. 2.

C. 5 .

D. 6 .

Câu 29: Tìm tập hợp tất cả các giá trị của tham số thực m để hàm số y=\frac{1}{3} x^{3}+m x^{2}+4 x-m\(y=\frac{1}{3} x^{3}+m x^{2}+4 x-m\) đồng biến trên khoảng (-\infty ;+\infty).\((-\infty ;+\infty).\)

A. [-2 ; 2]

B. (-\infty ; 2).\((-\infty ; 2).\)

C. (-\infty ;-2]\((-\infty ;-2]\)

D. [2 ;+\infty)\([2 ;+\infty)\)

Câu 30: Cho hàm số y=-\frac{1}{3} x^{3}+2 x^{2}+(2 a+1) x-3 a+2\(y=-\frac{1}{3} x^{3}+2 x^{2}+(2 a+1) x-3 a+2\) ( a là tham số). Với giá trị nào của a thì hàm số nghịch biến trên R.

A. a \leq 1\(a \leq 1\)

B. a \geq-\frac{5}{2}\(a \geq-\frac{5}{2}\)

C. a \leq-\frac{5}{2}.\(a \leq-\frac{5}{2}.\)

D.a \geq 1.\(a \geq 1.\)

Câu 31: Tìm tất cả các giá trị của m để hàm số y=(m-1) x^{3}-3(m-1) x^{2}+3 x+2\(y=(m-1) x^{3}-3(m-1) x^{2}+3 x+2\) đồng biến biến trên R?

A. 1<m ≤ 2.

B. 1<m<2.

C. 1 \leq m \leq 2.\(1 \leq m \leq 2.\)

D. 1 \leq m<2\(1 \leq m<2\)

Câu 32: Giá trị của m để hàm số y=\frac{1}{3} x^{3}-2 m x^{2}+(m+3) x-5+m\(y=\frac{1}{3} x^{3}-2 m x^{2}+(m+3) x-5+m\) đồng biến trên R là:

A. -\frac{3}{4} \leq m \leq 1\(A. -\frac{3}{4} \leq m \leq 1\)

B. m \leq-\frac{3}{4}\(B. m \leq-\frac{3}{4}\)

D. m \geq 1.\(D. m \geq 1.\)

Dạng 4. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước

Câu 33: Có bao nhiêu giá trị nguyên của tham số m để hàm số y=\frac{x+2}{x+3 m}\(y=\frac{x+2}{x+3 m}\) đồng biến trên khoảng (-\infty ;-6)\((-\infty ;-6)\).

A. 2

B. 6

C. Vô số

D. 1

Câu 34: Có bao nhiêu giá trị nguyên của tham số m để hàm số y=\frac{x+1}{x+3 m}\(y=\frac{x+1}{x+3 m}\) nghịch biến trên khoảng (6 ;+\infty)\((6 ;+\infty)\)?

A. 0

B. 6

C. 3

D. Vô số

Câu 35: Có bao nhiêu giá trị nguyên của tham số m để hàm số y=\frac{x+2}{x+5 m}\(y=\frac{x+2}{x+5 m}\)đồng biến trên khoảng (-\infty ;-10)\((-\infty ;-10)\)?

A. 2

B. Vô số

C. 1

D. 3

Câu 36: Cho hàm số y=\frac{m x+4 m}{x+m}\(y=\frac{m x+4 m}{x+m}\) với m la tham số. Gọi S la tâp hợp tất cả các giá trị nguyên của m để hàm số ngḥich biến trên các khoảng xác đinh. Tìm số phần tử của S.

A. 4

B. Vô số

C. 3

D. 5

Câu 37: Có bao nhiêu giá trị nguyên của tham số m để hàm số y=\frac{x+6}{x+5 m}\(y=\frac{x+6}{x+5 m}\) nghịch biến trên khoảng (10 ;+\infty)\((10 ;+\infty)\)?

A. Vô số

B. 4

C. 5

D. 3

.....................................................

Tài liệu vẫn còn, mời bạn tải về để xem trọn bộ tài liệu Các dạng bài tập tính đơn điệu của hàm số!

Chia sẻ bởi: 👨 Trịnh Thị Thanh
Liên kết tải về

Link Download chính thức:

Tìm thêm: Toán 12
Sắp xếp theo
👨

Tài liệu tham khảo khác

Chủ đề liên quan

Có thể bạn quan tâm

Xem thêm

Mới nhất trong tuần

Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ