3296 bài tập trắc nghiệm thể tích khối đa diện (Có đáp án) Ôn tập môn Toán lớp 12

Tải về Bình luận

TOP 3296 bài tập trắc nghiệm thể tích khối đa diện là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 12 tham khảo.

Trắc nghiệm thể tích khối đa diện gồm 296 trang tổng hợp các dạng bài tập trắc nghiệm thường xuất hiện trong các đề thi THPT Quốc gia qua các năm có đáp án kèm theo. Hi vọng qua tài liệu này giúp các bạn lớp 12 học tập chủ động, nâng cao kiến thức để đạt kết quả cao trong kì thi THPT Quốc gia sắp tới. Bên cạnh đó các bạn xem thêm: Bài tập phương trình phức, Bài tập thể tích khối chóp có một cạnh bên vuông góc với đáy, 572 câu trắc nghiệm chuyên đề Hàm số nâng cao.

3296 bài tập trắc nghiệm thể tích khối đa diện

Câu 1. Cho khối chóp S . ABC có đáy là tam giác đều canh a, SA = $\sqrt{3}$ $\sqrt{3}$ cạnh bên SA vuông góc với đáy. Thề tích của khối chóp S . ABC bằng

A. $\frac{a^{3} \sqrt{3}}{2}$ $\frac{a^{3} \sqrt{3}}{2}$

B. $\frac{a^{3}}{2}$ $\frac{a^{3}}{2}$

C. $\frac{a^{3} \sqrt{3}}{4}.$ $\frac{a^{3} \sqrt{3}}{4}.$

D. $\frac{a^{3}}{4}.$ $\frac{a^{3}}{4}.$

Câu 2. Cho khối chóp S.ABCD cạnh bên SA vuông góc với đáy, đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA = 3a. Thể tích của khối chóp S.ABCD bằng

A. $6 a^{3}.$ $6 a^{3}.$

B. $\frac{a^{3}}{3}$ $\frac{a^{3}}{3}$

C. $2 a^{3}.$ $2 a^{3}.$

D. $a^{3}.$ $a^{3}.$

Câu 3. Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và đáy bằng 30^O. Thể tích khối chóp S.ABC bằng

A. $\frac{a^{3} \sqrt{2}}{18}$ $\frac{a^{3} \sqrt{2}}{18}$

B. $\frac{a^{3} \sqrt{2}}{36}$ $\frac{a^{3} \sqrt{2}}{36}$

C. $\frac{a^{3} \sqrt{3}}{18}.$ $\frac{a^{3} \sqrt{3}}{18}.$

D. $\frac{a^{3} \sqrt{3}}{36}.$ $\frac{a^{3} \sqrt{3}}{36}.$

Câu 4. Cho khối chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, đường cao SO. Biết $S O=\frac{a \sqrt{2}}{2}$ $S O=\frac{a \sqrt{2}}{2}$ thể tích khối chóp S . ABCD bằng

A. $\frac{a^{3} \sqrt{2}}{6}$ $\frac{a^{3} \sqrt{2}}{6}$

B. $\frac{a^{3} \sqrt{2}}{3}$ $\frac{a^{3} \sqrt{2}}{3}$

C. $\frac{a^{3} \sqrt{2}}{2}$ $\frac{a^{3} \sqrt{2}}{2}$

D. $\frac{a^{3} \sqrt{3}}{4}$ $\frac{a^{3} \sqrt{3}}{4}$

Câu 5. Cho khối chóp S.ABC có AB = 5 cm, BC = 4 cm, CA = 7 cm. Các mặt bên tạo với mặt phẳng đáy (ABC) một góc 30 độ. Thể tích khối chóp S.ABC bằng

A. $\frac{4 \sqrt{2}}{3} c m^{3}$ $\frac{4 \sqrt{2}}{3} c m^{3}$

B. $\frac{4 \sqrt{3}}{3} c m^{3}.$ $\frac{4 \sqrt{3}}{3} c m^{3}.$

C. $\frac{4 \sqrt{6}}{3} \mathrm{cm}^{3}.$ $\frac{4 \sqrt{6}}{3} \mathrm{cm}^{3}.$

D. $\frac{4 \sqrt{3}}{4} \mathrm{cm}^{3}.$ $\frac{4 \sqrt{3}}{4} \mathrm{cm}^{3}.$

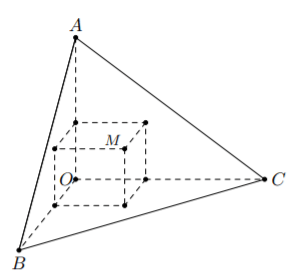
Câu 6. Có một khối gỗ dạng hình chóp O.ABC có OA, OB, OC đôi một vuông góc với nhau, OA = 3 cm, OB = 6 cm, OC = 12 cm. Trên mặt (ABC) người ta đánh dấu một điểm M sau đó người ta cắt gọt khối gỗ để thu được một hình hộp chữ nhật có OM là một đường chéo đồng thời hình hộp có 3 mặt nằm trên 3 mặt của tứ diện (xem hình vẽ). Thể tích lớn nhất của khối gỗ hình hộp chữ nhật bằng

A. 8 cm³

B 24 cm³

C 12 cm³

D 36 cm³

Câu 7. Cho khối chóp tam giác S.ABC có cạnh bên SA vuông góc với mặt phẳng (ABC), đáy là tam giác ABC cân tại A, độ dài trung tuyến AD bằng a, cạnh bên SB tạo với đáy góc 30◦ và tạo với mặt phẳng (SAD) góc 30 độ. Thể tích khối chóp S.ABC bằng:

A. $\frac{a^{3}}{3}$ $\frac{a^{3}}{3}$

B. $\frac{a^{3} \sqrt{3}}{3}$ $\frac{a^{3} \sqrt{3}}{3}$

C. $\frac{a^{3} \sqrt{3}}{6}$ $\frac{a^{3} \sqrt{3}}{6}$

D. $\frac{a^{3}}{6}.$ $\frac{a^{3}}{6}.$

Câu 8. Cho lăng trụ đều ABC $A^{\prime} B^{\prime} C^{\prime}$ $A^{\prime} B^{\prime} C^{\prime}$. Biết rằng góc giữa (A'BC) và (ABC) là 30 độ
tam giác A'BC có diện tích bằng 2. Thể tích khối lăng trụ ABC.A'B'C bằng

A. $2 \sqrt{6}.$ $2 \sqrt{6}.$

B. $\frac{\sqrt{6}}{2}$ $\frac{\sqrt{6}}{2}$

C. 2

D. $\sqrt{3}$ $\sqrt{3}$

Câu 9. Cho một hình chóp tam giác đều có cạnh bằng a, góc giữa canh bên và mặt phẳng dáy bằng 60 độ. Thể tích khối chóp đó là:

A. $\frac{a^{3} \sqrt{3}}{12}.$ $\frac{a^{3} \sqrt{3}}{12}.$

B. $\frac{a^{3} \sqrt{3}}{36}.$ $\frac{a^{3} \sqrt{3}}{36}.$

C. $\frac{a^{3}}{12}.$ $\frac{a^{3}}{12}.$

D. $\frac{a^{3}}{36}.$ $\frac{a^{3}}{36}.$

Câu 10. Cho hình chóp S.ABC có đáy là tam giác vuông cân tại C, cạnh bên SA vuông góc với mặt phẳng đáy, biết AB = 4a, SB = 6a. Thể tích khối chóp S.ABC là V. Tỉ số $\frac{4 a^{3}}{3 V}$ $\frac{4 a^{3}}{3 V}$ có giá trị là

A. $\frac{\sqrt{5}}{10}$ $\frac{\sqrt{5}}{10}$

B. $\frac{3 \sqrt{5}}{8}$ $\frac{3 \sqrt{5}}{8}$

C. $\frac{\sqrt{5}}{8}$ $\frac{\sqrt{5}}{8}$

D. $\frac{\sqrt{5}}{160}$ $\frac{\sqrt{5}}{160}$

Câu 11. Thể tích của khối lăng trụ đứng tam giác đều có tất cả các cạnh bằng a bằng

A. $\frac{a^{3} \sqrt{2}}{3}$ $\frac{a^{3} \sqrt{2}}{3}$

B. $\frac{a^{3}}{3}$ $\frac{a^{3}}{3}$

C. $\frac{a^{3} \sqrt{3}}{4}.$ $\frac{a^{3} \sqrt{3}}{4}.$

D. $\frac{a^{3} \sqrt{3}}{6}$ $\frac{a^{3} \sqrt{3}}{6}$

Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Điểm M, N theo thứ là trung điểm của SA, SB. Tỉ số thể tích $\frac{V_{S . C D M N}}{V_{S . C D A B}}$ $\frac{V_{S . C D M N}}{V_{S . C D A B}}$ là:

A. $\frac{5}{8}$ $\frac{5}{8}$

B. $\frac{3}{8}$ $\frac{3}{8}$

C. $\frac{1}{4}$ $\frac{1}{4}$

D. $\frac{1}{2}$ $\frac{1}{2}$

................

Tải file tài liệu để xem thêm nội dung chi tiết

Chia sẻ bởi:

Trịnh Thị Thanh

Tải về

Liên kết tải về

3296 bài tập trắc nghiệm thể tích khối đa diện (Có đáp án) 2,4 MB Tải về

Chọn file cần tải:

395 bài tập trắc nghiệm thể tích khối đa diện 2,4 MB Tải về

Tìm thêm: Toán 12

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!