Toán 9 Bài 2: Bất phương trình bậc nhất một ẩn Giải Toán 9 Cánh diều tập 1 trang 35, 36, 37, 38, 39, 40, 41

Bài trước

Mục lục

Bài sau

Giải Toán 9 Bài 2: Bất phương trình bậc nhất một ẩn là tài liệu vô cùng hữu ích giúp các em học sinh lớp 9 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 9 Cánh diều tập 1 trang 35, 36, 37, 38, 39, 40, 41.

Giải bài tập Toán 9 Cánh diều tập 1 Bài 2 - Chương II: Bất đẳng thức, bất phương trình bậc nhất một ẩn được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Toán 9 Bài 2: Bất phương trình bậc nhất một ẩn Cánh diều

Giải Toán 9 Cánh diều Tập 1 trang 40, 41

Giải Toán 9 Cánh diều Tập 1 trang 40, 41

Bài 1

Kiểm tra xem số nào là nghiệm của mỗi bất phương trình tương ứng sau đây.

a) x² – 3x + 2 > 0 với x = –3; x = 1,5.

b) 2 – 2x < 3x + 1 với x = $\frac{2}{5}$ $\frac{2}{5}$; x = $\frac{1}{5}$ $\frac{1}{5}$

Hướng dẫn giải

a) ⦁ Thay x = –3 vào bất phương trình đã cho, ta được:

(–3)² – 3.(–3) + 2 > 0 hay 20 > 0 là khẳng định đúng.

Do đó x = –3 là nghiệm của bất phương trình đã cho.

⦁ Thay x = 1,5 vào bất phương trình đã cho, ta được:

1,5² – 3.1,5 + 2 > 0 hay –0,25 > 0 là khẳng định không đúng.

Do đó x = 1,5 không là nghiệm của bất phương trình đã cho.

Bài 2

Giải các bất phương trình:

a) 2x + 6 > 1;

b) 0,6x + 2 > 6x + 9;

c) 1,7x + 4 ≥ 2 + 1,5x.

Hướng dẫn giải

$\begin{array}{l}2x + 6 > 1\\2x > - 5\\x > \frac{{ - 5}}{2}\end{array}$ $\begin{array}{l}2x + 6 > 1\\2x > - 5\\x > \frac{{ - 5}}{2}\end{array}$

Vậy nghiệm của bất phương trình là $x > \frac{{ - 5}}{2}.$ $x > \frac{{ - 5}}{2}.$

$\begin{array}{l}0,6x + 2 > 6x + 9\\0,6x + 2 - 6x - 9 > 0\\ - 5,4x - 7 > 0\\ - 5,4x > 7\\x < - \frac{{35}}{{27}}\end{array}$ $\begin{array}{l}0,6x + 2 > 6x + 9\\0,6x + 2 - 6x - 9 > 0\\ - 5,4x - 7 > 0\\ - 5,4x > 7\\x < - \frac{{35}}{{27}}\end{array}$

Vậy nghiệm của bất phương trình là $x < - \frac{{35}}{{27}}.$ $x < - \frac{{35}}{{27}}.$

$\begin{array}{l}1,7x + 4 \ge 2 + 1,5x\\1,7x + 4 - 2 - 1,5x \ge 0\\0,2x + 2 \ge 0\\0,2x \ge - 2\\x \ge - 10\end{array}$ $\begin{array}{l}1,7x + 4 \ge 2 + 1,5x\\1,7x + 4 - 2 - 1,5x \ge 0\\0,2x + 2 \ge 0\\0,2x \ge - 2\\x \ge - 10\end{array}$

Vậy nghiệm của bất phương trình là $x \ge - 10.$ $x \ge - 10.$

Bài 3

Giải các bất phương trình:

a. $\frac{{8 - 3x}}{2} - x < 5$ $\frac{{8 - 3x}}{2} - x < 5$

b. $3 - 2x - \frac{{6 + 4x}}{3} > 0$ $3 - 2x - \frac{{6 + 4x}}{3} > 0$

c. $0,7x + \frac{{2x - 4}}{3} - \frac{x}{6} > 1$ $0,7x + \frac{{2x - 4}}{3} - \frac{x}{6} > 1$

Hướng dẫn giải

$\begin{array}{*{20}{l}}{\frac{{8 - 3x}}{2} - x < 5}\\{\frac{{8 - 3x}}{2} - \frac{{2x}}{2} < \frac{{10}}{2}}\\{\frac{{8 - 3x - 2x}}{2} - \frac{{10}}{2} < 0}\\{\frac{{8 - 3x - 2x - 10}}{2} < 0}\\{\frac{{ - 5x - 2}}{2} < 0}\\{ - 5x - 2 < 0}\\{ - 5x < 2}\\{x > \frac{{ - 2}}{5}}\end{array}$ $\begin{array}{*{20}{l}}{\frac{{8 - 3x}}{2} - x < 5}\\{\frac{{8 - 3x}}{2} - \frac{{2x}}{2} < \frac{{10}}{2}}\\{\frac{{8 - 3x - 2x}}{2} - \frac{{10}}{2} < 0}\\{\frac{{8 - 3x - 2x - 10}}{2} < 0}\\{\frac{{ - 5x - 2}}{2} < 0}\\{ - 5x - 2 < 0}\\{ - 5x < 2}\\{x > \frac{{ - 2}}{5}}\end{array}$

Vậy nghiệm của bất phương trình là $x > \frac{{ - 2}}{5}.$ $x > \frac{{ - 2}}{5}.$

$\begin{array}{*{20}{l}}{3 - 2x - \frac{{6 + 4x}}{3} > 0}\\{\frac{9}{3} - \frac{{6x}}{3} - \frac{{6 + 4x}}{3} > 0}\\{\frac{{9 - 6x - 6 - 4x}}{3} > 0}\end{array}$ $\begin{array}{*{20}{l}}{3 - 2x - \frac{{6 + 4x}}{3} > 0}\\{\frac{9}{3} - \frac{{6x}}{3} - \frac{{6 + 4x}}{3} > 0}\\{\frac{{9 - 6x - 6 - 4x}}{3} > 0}\end{array}$

$\begin{array}{*{20}{l}}{\frac{{ - 10x + 3}}{3} > 0}\\\begin{array}{l} - 10x + 3 > 0\\ - 10x > - 3\end{array}\\{x < \frac{3}{{10}}}\end{array}$ $\begin{array}{*{20}{l}}{\frac{{ - 10x + 3}}{3} > 0}\\\begin{array}{l} - 10x + 3 > 0\\ - 10x > - 3\end{array}\\{x < \frac{3}{{10}}}\end{array}$

Vậy nghiệm của bất phương trình là $x < \frac{3}{{10}}.$ $x < \frac{3}{{10}}.$

$\begin{array}{*{20}{l}}{0,7x + \frac{{2x - 4}}{3} - \frac{x}{6} > 1}\\\begin{array}{l}\frac{{4,2x}}{6} + \frac{{2.\left( {2x - 4} \right)}}{6} - \frac{x}{6} > \frac{6}{6}\\\frac{{4,2x + 4x - 8 - x - 6}}{6} > 0\end{array}\\{4,2x + 4x - 8 - x - 6 > 0}\\{7,2x - 14 > 0}\\{7,2x > 14}\\{x > \frac{{35}}{{18}}}\end{array}$ $\begin{array}{*{20}{l}}{0,7x + \frac{{2x - 4}}{3} - \frac{x}{6} > 1}\\\begin{array}{l}\frac{{4,2x}}{6} + \frac{{2.\left( {2x - 4} \right)}}{6} - \frac{x}{6} > \frac{6}{6}\\\frac{{4,2x + 4x - 8 - x - 6}}{6} > 0\end{array}\\{4,2x + 4x - 8 - x - 6 > 0}\\{7,2x - 14 > 0}\\{7,2x > 14}\\{x > \frac{{35}}{{18}}}\end{array}$

Vậy nghiệm của bất phương trình là $x > \frac{{35}}{{18}}.$ $x > \frac{{35}}{{18}}.$

Bài 4

Tìm số thực dương x sao cho ở Hình 2 chu vi của hình tam giác lớn hơn chu vi của hình chữ nhật:

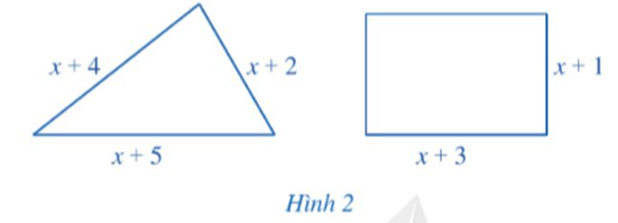
Hình 2

Hướng dẫn giải

Chu vi của hình tam giác là: (x + 4) + (x + 2) + (x + 5) = 3x + 11.

Chu vi của hình chữ nhật là: 2.(x + 1 + x + 3) = 2.(2x + 4) = 4x + 8.

Theo bài, chu vi hình tam giác lớn hơn chu vi của hình chữ nhật nên ta có bất phương trình: 3x + 11 > 4x + 8.

Giải bất phương trình:

3x + 11 > 4x + 8

3x – 4x > 8 – 11

–x > –3

x < 3.

Mà x là số thực dương nên x > 0.

Vậy 0 < x < 3.

Bài 5

Một kho chứa 100 tấn xi măng, mỗi ngày đều xuất đi 20 tấn xi măng. Gọi x là số ngày xuất xi măng của kho đó. Tìm x sao cho sau x ngày xuất hàng, khối lượng xi măng còn lại trong kho ít nhất là 10 tấn.

Hướng dẫn giải

Sau x ngày, khối lượng xi măng xuất đi là: 20x (tấn).

Khi đó, khối lượng xi măng còn lại trong kho là: 100 – 20x (tấn).

Theo bài, khối lượng xi măng còn lại trong kho ít nhất là 10 tấn nên ta có bất phương trình: 100 – 20x ≥ 10.

Giải bất phương trình:

100 – 20x ≥ 10

– 20x ≥ –90

x ≤ 4,5.

Vậy x ≤ 4,5.

Chia sẻ bởi: