Toán 9 Bài tập cuối chương V Giải Toán 9 Cánh diều tập 1 trang 124, 125

Bài trước

Mục lục

Bài sau

Giải Toán 9 Bài tập cuối chương V: Đường tròn là tài liệu vô cùng hữu ích giúp các em học sinh lớp 9 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 9 Cánh diều tập 1 trang 124, 125.

Giải bài tập Toán 9 Cánh diều tập 1 trang 124, 125 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Toán 9 Bài tập cuối chương V Cánh diều

Giải Toán 9 Cánh diều Tập 1 trang 124, 125

Giải Toán 9 Cánh diều Tập 1 trang 124, 125

Bài 1

Trong Hình 92, cho các điểm $A,B,C,D,E$ thuộc đường tròn $\left( O \right)$ $\left( O \right)$.

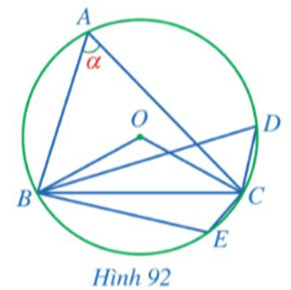
Bài tập cuối chương V

a) Số đo góc $BOC$ là:

A. $\alpha$ $\alpha$

B. $2\alpha$ $2\alpha$

C. $180^\circ - \alpha$ $180^\circ - \alpha$

B. $180^\circ - 2\alpha$ $180^\circ - 2\alpha$

b) Số đo góc $BDC$ là:

A. $\alpha$ $\alpha$

B. $\frac{\alpha }{2}$ $\frac{\alpha }{2}$

C. $180^\circ - \alpha$ $180^\circ - \alpha$

D. $180^\circ - \frac{\alpha }{2}$ $180^\circ - \frac{\alpha }{2}$

c) Số đo góc $BEC$ là:

A. $\alpha$ $\alpha$

B. $2\alpha$ $2\alpha$

C. $180^\circ - \alpha$ $180^\circ - \alpha$

D. $360^\circ - \alpha$ $360^\circ - \alpha$

Hướng dẫn giải

a) Chọn đáp án B.

b) Chọn đáp án A.

c) Chọn đáp án C.

Bài 2

a) Độ dài cung tròn có số đo $30^\circ$ $30^\circ$ của đường tròn có bán kính R là:

A. $\frac{{\pi R}}{{180}}$ $\frac{{\pi R}}{{180}}$

B. $\frac{{\pi R}}{{360}}$ $\frac{{\pi R}}{{360}}$

C. $30\pi R$ $30\pi R$

D. $\frac{{\pi R}}{6}$ $\frac{{\pi R}}{6}$

b) Diện tích của hình quạt tròn tâm O, bán kính R, cung có số đo $45^\circ$ $45^\circ$ là:

A. $\frac{{\pi {R^2}}}{{45}}$ $\frac{{\pi {R^2}}}{{45}}$

B. $\frac{{\pi {R^2}}}{4}$ $\frac{{\pi {R^2}}}{4}$

C. $\frac{{\pi {R^2}}}{8}$ $\frac{{\pi {R^2}}}{8}$

D. $\frac{{\pi {R^2}}}{{16}}$ $\frac{{\pi {R^2}}}{{16}}$

Hướng dẫn giải

a) Chọn đáp án D.

b) Chọn đáp án C.

Bài 3

Cho hình vuông $ABCD$ cạnh $r$ và đường tròn $\left( {C;r} \right)$ $\left( {C;r} \right)$ giả sử $M$ là một điểm nằm trên đường tròn $\left( {C;r} \right)$ $\left( {C;r} \right)$ sao cho điểm $M$ nằm trong hình vuông $ABCD$. Tiếp tuyến của đường tròn $\left( {C;r} \right)$ $\left( {C;r} \right)$ tại tiếp điểm $M$ cắt các đoạn thẳng $AB,AD$ lần lượt tại $N,P$. Chứng minh:

a) Các đường thẳng $NB,PD$ là các tiếp tuyến của đường tròn $\left( {C;r} \right)$ $\left( {C;r} \right)$.

b) $\widehat {NCP} = \widehat {NCB} + \widehat {PCD} = 45^\circ$ $\widehat {NCP} = \widehat {NCB} + \widehat {PCD} = 45^\circ$.

Hướng dẫn giải

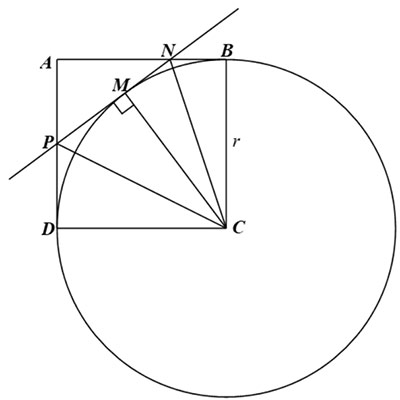
Bài tập cuối chương V

a) Do $ABCD$ là hình vuông nên $AB = BC = CD = AD = r$; $AB \bot BC$ $AB \bot BC$ hay $NB \bot BC$ $NB \bot BC$; $AD \bot CD$ $AD \bot CD$ hay $PD \bot CD$ $PD \bot CD$.

Xét $\left( C \right)$ $\left( C \right)$ có:

+ $B \in \left( C \right);NB \bot BC \Rightarrow NB$ $B \in \left( C \right);NB \bot BC \Rightarrow NB$ là tiếp tuyến của $\left( C \right)$ $\left( C \right)$.

+ $D \in \left( C \right);PD \bot CD \Rightarrow PD$ $D \in \left( C \right);PD \bot CD \Rightarrow PD$ là tiếp tuyến của $\left( C \right)$ $\left( C \right)$.

b) Do $MP$ và $PD$ là hai tiếp tuyến cắt nhau tại $P$ nên $CP$ là tia phân giác của $\widehat {MCD} \Rightarrow \widehat {MCP} = \widehat {PCD}$ $\widehat {MCD} \Rightarrow \widehat {MCP} = \widehat {PCD}$ (1).

Do $MN$ nà $NB$ là hai tiếp tuyến cắt nhau tại $N$ nên $CN$ là tia phân giác của $\widehat {MCB} \Rightarrow \widehat {MCN} = \widehat {BCN}$ $\widehat {MCB} \Rightarrow \widehat {MCN} = \widehat {BCN}$(2).

Từ (1) và (2) suy ra $\widehat {MCP} + \widehat {MCN} = \widehat {PCD} + \widehat {BCN}$ $\widehat {MCP} + \widehat {MCN} = \widehat {PCD} + \widehat {BCN}$ $\Rightarrow \widehat {PCN} = \widehat {PCD} + \widehat {BCN}$ $\Rightarrow \widehat {PCN} = \widehat {PCD} + \widehat {BCN}$.

Lại có: $\widehat {PCN} + \widehat {PCD} + \widehat {PCN} = 90^\circ$ $\widehat {PCN} + \widehat {PCD} + \widehat {PCN} = 90^\circ$ hay $\widehat {PCN} + \widehat {PCN} = 90^\circ \Rightarrow \widehat {PCN} = 45^\circ$ $\widehat {PCN} + \widehat {PCN} = 90^\circ \Rightarrow \widehat {PCN} = 45^\circ$.

Vậy $\widehat {PCN} = \widehat {PCD} + \widehat {BCN} = 45^\circ$ $\widehat {PCN} = \widehat {PCD} + \widehat {BCN} = 45^\circ$.

Bài 4

Chứng minh trong một đường tròn:

a) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy;

b) Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy;

c) Hai dây bằng nhau thì cách đều tâm;

d) Hai dây cách đều tâm thì bằng nhau.

Hướng dẫn giải

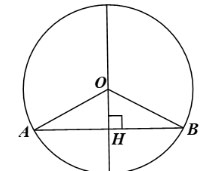
Bài tập cuối chương V

Gọi (O) là đường tròn có đường kính vuông góc với dây AB tại H.

Xét ∆OAB có OA = OB = R nên ∆OAB cân tại O.

∆OAB cân tại O có OH là đường cao (do OH ⊥ AB) nên đồng thời là đường trung tuyến của tam giác. Do đó H là trung điểm của AB.

Vậy đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.

Bài tập cuối chương V

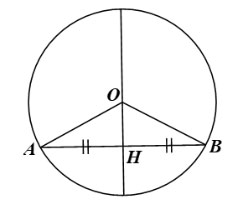
Gọi (O) là đường tròn có đường kính đi qua trung điểm H của dây AB.

Xét ∆OAB có OA = OB = R nên ∆OAB cân tại O.

∆OAB cân tại O có OH là đường trung tuyến nên đồng thời là đường cao của tam giác. Do đó OH ⊥ AB tại H.

Vậy đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.

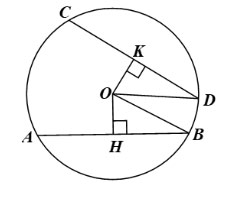
Bài tập cuối chương V

Gọi (O) là đường tròn có hai dây AB, CD. Gọi OH, OK lần lượt là khoảng cách từ O đến AB, CD. Khi đó OH ⊥ AB tại H và OK ⊥ CD tại K.

Do đó, theo kết quả của câu a, ta có: H, K lần lượt là trung điểm của AB, CD.

Suy ra HB = $\frac{1}{2}$ $\frac{1}{2}$AB và KD = $\frac{1}{2}$ $\frac{1}{2}$CD.

Mà AB = CD nên HB = KD. (1)

Xét ∆OHB vuông tại H, ta có: OB² = OH² + HB² (định lí Pythagore).

Suy ra OH² = OB² – HB² = R² – HB². (2)

Xét ∆OKD vuông tại H, ta có: OD² = OK² + KD² (định lí Pythagore).

Suy ra OK² = OD² – KD² = R² – KD². (3)

Từ (1), (2) và (3) suy ra OH² = OK², hay OH = OK.

Vậy hai dây bằng nhau thì cách đều tâm.

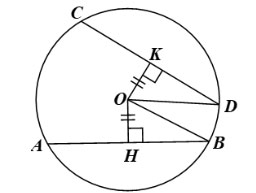
Bài tập cuối chương V

Gọi (O) là đường tròn có hai dây AB, CD bằng nhau. Gọi OH, OK lần lượt là khoảng cách từ O đến AB, CD. Khi đó OH ⊥ AB tại H, OK ⊥ CD tại K.

Do đó, theo kết quả của câu a, ta có: H, K lần lượt là trung điểm của AB, CD.

Suy ra AB = 2HB và CD = 2KD.

Theo bài, OH = OK, suy ra OH² = OK². (1)

Xét ∆OHB vuông tại H, ta có: OB² = OH² + HB² (định lí Pythagore).

Suy ra HB² = OB² – OH² = R² – OH². (2)

Xét ∆OKD vuông tại H, ta có: OD² = OK² + KD² (định lí Pythagore).

Suy ra KD² = OD² – OK² = R² – OK². (3)

Từ (1), (2) và (3) suy ra HB² = KD², hay HB = KD.

Do đó 2HB = 2KD hay AB = CD.

Vậy hai dây cách đều tâm thì bằng nhau.

Bài 5

Cho hai đường tròn $\left( {I;r} \right)$ $\left( {I;r} \right)$ và $\left( {K;R} \right)$ $\left( {K;R} \right)$ tiếp xúc ngoài với nhau tại $P$ với $R \ne r$ $R \ne r$, đường thẳng $a$ lần lượt tiếp xúc với $\left( {I;r} \right)$ $\left( {I;r} \right)$ và $\left( {K;R} \right)$ $\left( {K;R} \right)$ tại $A$ và $B,a$ cắt $KI$ tại $O$. Đường thẳng qua $P$ vuông góc với $IK$ cắt đường thẳng $a$ tại $M$. Chứng minh:

a) $\frac{{OI}}{{OK}} = \frac{r}{R}$ $\frac{{OI}}{{OK}} = \frac{r}{R}$;

b) $AB = 2MP$;

c) $\widehat {IMK} = 90^\circ$ $\widehat {IMK} = 90^\circ$.

Hướng dẫn giải

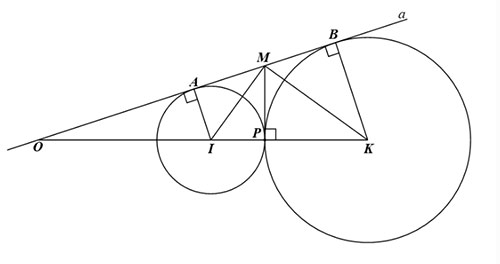
Bài tập cuối chương V

a) Do $AI$ là tiếp tuyến của $\left( I \right)$ $\left( I \right)$ nên $AI \bot AB$ $AI \bot AB$

Do $BK$ là tiếp tuyến của $\left( K \right)$ $\left( K \right)$ nên $KB \bot AB$ $KB \bot AB$

Từ đó suy ra $AI//BK$

Xét tam giác $OBK$ có: $AI//BK \Rightarrow \frac{{OI}}{{OK}} = \frac{{AI}}{{BK}} = \frac{r}{R}$ $AI//BK \Rightarrow \frac{{OI}}{{OK}} = \frac{{AI}}{{BK}} = \frac{r}{R}$ (định lí Thalet).

b) Xét $\left( I \right)$ $\left( I \right)$ có $MP,MA$ là hai tiếp tuyến cắt nhau

$\Rightarrow MP = MA$ $\Rightarrow MP = MA$(1).

Xét $\left( K \right)$ $\left( K \right)$ có $MP,MB$ là hai tiếp tuyến cắt nhau

$\Rightarrow MP = MB$ $\Rightarrow MP = MB$(2).

Từ (1) và (2) suy ra $MP + MP = MA + MB \Rightarrow 2MP = AB$ $MP + MP = MA + MB \Rightarrow 2MP = AB$

c) Do $AI//BK \Rightarrow \widehat {OIA} = \widehat {IKB}$ $AI//BK \Rightarrow \widehat {OIA} = \widehat {IKB}$ (2 góc đồng vị).

Mà $\widehat {AIK} + \widehat {OAI} = 180^\circ$ $\widehat {AIK} + \widehat {OAI} = 180^\circ$ (2 góc kề bù) nên $\widehat {AIK} + \widehat {IKB} = 180^\circ$ $\widehat {AIK} + \widehat {IKB} = 180^\circ$ (3).

Do $MP,MA$ là hai tiếp tuyến cắt nhau

$\Rightarrow IM$ $\Rightarrow IM$ là phân giác $\widehat {AIP} \Rightarrow \widehat {MIP} = \frac{1}{2}\widehat {AIP}$ $\widehat {AIP} \Rightarrow \widehat {MIP} = \frac{1}{2}\widehat {AIP}$ (4).

Do $MP,MB$ là hai tiếp tuyến cắt nhau

$\Rightarrow KM$ $\Rightarrow KM$ là phân giác $\widehat {IKP} \Rightarrow \widehat {MKP} = \frac{1}{2}\widehat {IKP}$ $\widehat {IKP} \Rightarrow \widehat {MKP} = \frac{1}{2}\widehat {IKP}$ (5).

Từ (3), (4) và (5) suy ra $\frac{1}{2}\widehat {AIP} + \frac{1}{2}\widehat {IKP} = \frac{1}{2}.180^\circ \Rightarrow \widehat {MIP} + \widehat {MKP} = 90^\circ$ $\frac{1}{2}\widehat {AIP} + \frac{1}{2}\widehat {IKP} = \frac{1}{2}.180^\circ \Rightarrow \widehat {MIP} + \widehat {MKP} = 90^\circ$

Xét tam giác $IMK$ có: $\widehat {MIP} + \widehat {MKP} = 90^\circ \Rightarrow \widehat {IMK} = 90^\circ$ $\widehat {MIP} + \widehat {MKP} = 90^\circ \Rightarrow \widehat {IMK} = 90^\circ$

Bài 6

Mặt đĩa CD ở Hình 93 có dạng hình vành khuyên giới hạn bởi hai đường tròn có bán kính lần lượt là 1,5 cm và 6 cm. Hình vành khuyên đó có diện tích bằng bao nhiêu centimét vuông (làm tròn kết quả đến hàng đơn vị)?

Bài tập cuối chương V

Hướng dẫn giải

Diện tích mặt đĩa CD có dạng hình vành khuyên là:

S = π(6² – 1,5²) = 33,75π ≈ 106 (cm²).

Bài 7

Hình 94 mô tả mảnh vải có dạng một phần tư hình vành khuyên, trong đó hình vành khuyên giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là 3 dm và 5 dm. Diện tích của mảnh vải đó bằng bao nhiêu decimét vuông (làm tròn kết quả đến hàng phần mười)?

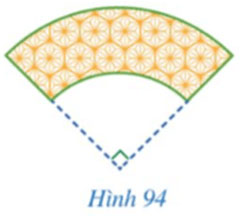
Bài tập cuối chương V

Hướng dẫn giải

Diện tích hình vành khuyên là:

$S = \frac{1}{4}\pi \left( {{5^2} - {3^2}} \right) = 4\pi \left( {d{m^2}} \right)$ $S = \frac{1}{4}\pi \left( {{5^2} - {3^2}} \right) = 4\pi \left( {d{m^2}} \right)$.

Diện tích cung tròn là:

$S = \frac{{\pi {R^2}.90}}{{360}} = \frac{{9\pi }}{4}\left( {d{m^2}} \right)$ $S = \frac{{\pi {R^2}.90}}{{360}} = \frac{{9\pi }}{4}\left( {d{m^2}} \right)$.

Diện tích mảnh vải là:

Bài 8

Logo ở Hình 95 có dạng một hình quạt tròn bán kính 8 cm và góc ở tâm bằng 60°. Tính diện tích mỗi hình sau (theo đơn vị centimét vuông và làm tròn kết quả đến hàng phần mười).

Bài tập cuối chương V

a) Toàn bộ logo;

b) Phần logo màu đỏ có dạng hình viên phân.

Bài 9

Hình 96 biểu diễn vùng biển được chiếu sáng bởi một hải đăng có dạng một hình quạt tròn với bán kính 18 dặm, cung AmB có số đo 245°.

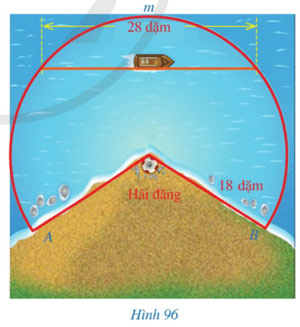
Bài tập cuối chương V

a) Hãy tính diện tích vùng biển có thể nhìn thấy ánh sáng từ hải đăng theo đơn vị kilômét vuông (lấy 1 dặm = 1 609 m và làm tròn kết quả đến hàng đơn vị).

b) Giả sử một con thuyền di chuyển dọc theo dây cung có độ dài 28 dặm của đường tròn với tâm là tâm của hình quạt tròn, bán kính là 18 dặm. Tính khoảng cách nhỏ nhất từ con thuyền đến hải đăng (theo đơn vị dặm và làm tròn kết quả đến hàng đơn vị).

Chia sẻ bởi: