Toán 12 Bài 9: Khoảng biến thiên và khoảng tứ phân vị Giải Toán 12 Kết nối tri thức trang 75 → 79

Giải Toán 12 Bài 9: Khoảng biến thiên và khoảng tứ phân vị là tài liệu vô cùng hữu ích giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 12 Kết nối tri thức với cuộc sống tập 1 trang 75, 76, 77, 78, 79.

Giải bài tập Toán 12 Kết nối tri thức tập 1 Bài 9 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 9 Chương III: Các số đặc trưng đo mức độ phân tán của mẫu số liệu ghép nhóm. Mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Giải Toán 12 Kết nối tri thức Tập 1 trang 78, 79

Bài 3.1

Thống kê số thẻ vàng của mỗi câu lạc bộ trong giải ngoại hạng Anh mùa giải 2021 – 2022 cho kết quả sau:

a) Hãy ghép nhóm dãy số liệu trên thành các nhóm có độ dài bằng nhau với nhóm đầu tiên là [40; 50).

b) Tính khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu gốc và mẫu số liệu ghép nhóm thu được ở câu a. Giá trị nào là giá trị chính xác? Giá trị nào là giá trị xấp xỉ?

Bài 3.2

Thu nhập theo tháng (đơn vị: triệu đồng) của người lao động ở hai nhà máy như sau:

Tính mức thu nhập trung bình của người lao động ở hai nhà máy trên. Dựa vào khoảng tứ phân vị, hãy xác định xem mức thu nhập của người lao động ở nhà máy nào biến động nhiều hơn.Hướng dẫn giải:

Chọn giá trị đại diện cho mỗi nhóm số liệu ta có:

Mức thu nhập trung bình của người lao động ở nhà máy A là:

\(\frac{6,5.20+9,5.35+12,5.45+15,5.35+18,5.20}{\left(20+35+45+35+20\right)}=12,5\)(triệu đồng)

Mức thu nhập trung bình của người lao động ở nhà máy B là:

\(\frac{6,5.17+9,5.23+12,5.30+15,5.23+18,5.17}{\left(17+23+30+23+17\right)}=12,5\) (triệu đồng)

Nhà máy A: Cỡ mẫu n = 155

\(Q_1=8+\frac{\frac{155}{4}-20}{35}.\left(11-8\right)\approx9,61\)

\(Q_3=14+\frac{\frac{155.3}{4}-100}{35}.\left(17-14\right)\approx 15,39\)

Khoảng tứ phân vị là: 15,39 - 9,61 = 5,78

Nhà máy B: Cỡ mẫu n = 110

\(Q_1=8+\frac{\frac{110}{4}-17}{23}.\left(11-8\right)\approx9,37\)

\(Q_3=14+\frac{\frac{110.3}{4}-70}{23}.\left(17-14\right)\approx 15,6\)

Khoảng tứ phân vị là: 15,6 - 9,37 = 6,23

Vậy dựa vào khoảng tứ phân vị thì có thể khẳng định thu nhập của người lao động ở nhà máy B phân tán hơn.

Bài 3.3

Bảng sau đây cho biết chiều cao của các học sinh lớp 12A và 12B.

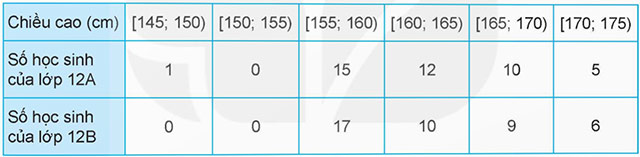
a) Tìm khoảng biến thiên, khoảng tứ phân vị cho các mẫu số liệu ghép nhóm về chiều cao của học sinh lớp 12A, 12B.

b) Để so sánh độ phân tán về chiều cao của học sinh hai lớp này ta nên dùng khoảng biến thiên hay khoảng tứ phân vị? Vì sao?

Hướng dẫn giải:

Lớp 12A.

Khoảng biến thiên: R₁ = 175 - 145 = 30

Cỡ mẫu n = 43

\(Q_1=155+\frac{\frac{43}{4}-1}{15}.\left(160-155\right)\approx158,25\)

\(Q_3=165+\frac{\frac{43,3}{4}-28}{10}.\left(170-165\right)\approx 167,125\)

Khoảng tứ phân vị là: 167,125 - 158,25 = 8,875

Lớp 12B.

Khoảng biến thiên: R₁ = 175 - 155 = 20

Cỡ mẫu n = 42

\(Q_1=155+\frac{\frac{42}{4}-0}{17}.\left(160-155\right)\approx158,09\)

\(Q_3=165+\frac{\frac{42}{4}-27}{9}.\left(170-165\right)\approx 167,5\)

Khoảng tứ phân vị là: 167,5 - 158,09 = 9,41

b) ta nên dùng khoảng tứ phân vị vì khoảng tứ phân vị không bị ảnh hưởng bởi các giá trị quá lớn hay quá bé.