Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số Giải Toán 12 Kết nối tri thức trang 5 → 14

Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số là tài liệu vô cùng hữu ích giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 12 Kết nối tri thức với cuộc sống tập 1 trang 5, 6, 7, 8, 9, 10, 11, 12, 13, 14.

Giải bài tập Toán 12 Kết nối tri thức tập 1 Bài 1 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 1 Chương I: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số. Mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Giải Toán 12 Kết nối tri thức Tập 1 trang 13, 14

Bài 1.1

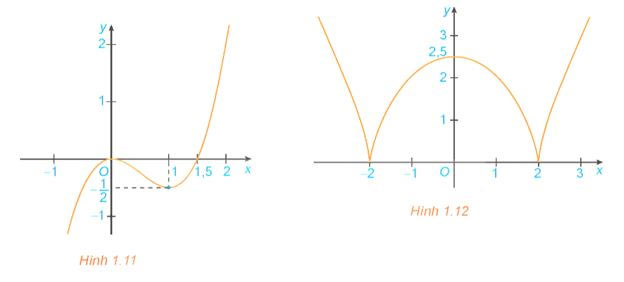
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:

a) Đồ thị hàm số \((y = {x^3} - \frac{3}{2} {x^2})\) (H.1.11);

b) Đồ thị hàm số \(y = \sqrt[3]{{{{( {{x^2} - 4} )}^2}}}\) (H.1.12).

Lời giải:

a) Tập xác định của hàm số là R.

Từ đồ thị hàm số Hình 1.11 suy ra:

• Hàm số đồng biến trên khoảng (- ∞; 0) và (1; + ∞)
• Hàm số nghịch biến trên khoảng (0; 1)

b) Tập xác định của hàm số là R.

Từ đồ thị hàm số Hình 1.12 suy ra:

• Hàm số đồng biến trên khoảng (- 2; 0) và (2; + ∞)
• Hàm số nghịch biến trên khoảng (- ∞; - 2) và (0; 2).

Bài 1.2

Xét sự đồng biến, nghịch biến của các hàm số sau:

a) \(y = \frac{1}{3}{x^3} - 2{x^2} + 3x + 1\)

b) \(y = - {x^3} + 2{x^2} - 5x + 3\)

a) \(y=\frac{1}{3}x^3-2x^2+3x+1\)

Tập xác định của hàm số là R.

Ta có: y' = x² - 4x + 3

y' = 0 \(\Leftrightarrow\) x = 1 hoặc x = 3.

Lập bảng biến thiên của hàm số:

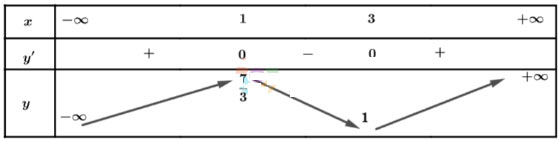
Từ bảng biến thiên, ta có:

Hàm số đồng biến trên các khoảng \(\left(-∞;1\right)\) và \(\left(3;+∞\right)\)

Hàm số nghịch biến trên các khoảng (1; 3).

b) y = - x³ + 2x² - 5x + 3.

Tập xác định của hàm số là R.

Ta có: y' = - 3x² + 4x - 5

= \(-3\left(x^2-\frac{4}{3}x+\frac{5}{3}\right)\)

\(=-3\left(x-\frac{2}{3}\right)^2-\frac{11}{3} <0\) với mọi x

Hàm số nghịch biến trên R.

Bài 1.3

Tìm các khoảng đơn điệu của các hàm số sau:

a) \(y = \frac{{2x - 1}}{{x + 2}}\);

b) \(y = \frac{{{x^2} + x + 4}}{{x - 3}}\).

Lời giải:

a) \(y=\frac{2x-1}{x+2}\)

Tập xác định của hàm số là R \ {- 2}

Ta có: \(y'=\frac{2\left(x+2\right)-\left(2x-1\right)}{\left(x+2\right)^2}=\frac{5}{\left(x+2\right)^2} >0\), với mọi x ≠ - 2.

Lập bảng biến thiên của hàm số:

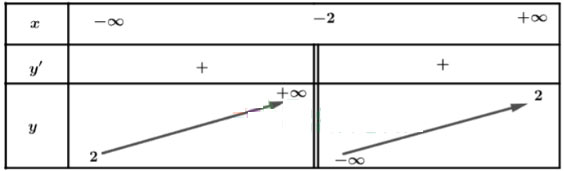
Từ bảng biến thiên, ta có: Hàm số đồng biến trên các khoảng \(\left(-∞;-2\right)\) và \(\left(-2;+∞\right)\)

b) \(y=\frac{x^2+x+4}{x-3}\)

Tập xác định của hàm số là R \ {3}

Ta có: \(y'=\frac{(2x+1)\left(x-3\right)-\left(x^2+x+4\right)}{\left(x-3\right)^2}=\frac{x^2-6x-7}{\left(x-3\right)^2}\)

y' = 0 \(\Leftrightarrow\) x= - 1 hoặc x = 7

Lập bảng biến thiên của hàm số:

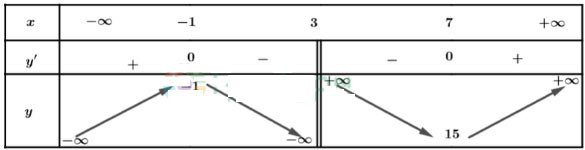
Từ bảng biến thiên, ta có:

Hàm số đồng biến trên các khoảng \(\left(-∞;-1\right)\) và \(\left(7;+∞\right)\)

Hàm số nghịch biến trên các khoảng (- 1; 3) và (3; 7)

Bài 1.4 

Xét chiều biến thiên của các hàm số sau:

a) \(y = \sqrt {4 - {x^2}} ;\)

b) \(y = \frac{x}{{{x^2} + 1}}\).

Lời giải:

a) \(y=\sqrt{4-x^2}\)

Tập xác định của hàm số là: [- 2; 2]

Ta có: \(y'=-\frac{x}{\sqrt{4-x^2}}\); y' > 0 với x ∈ (- 2; 0) và y' < 0 với (0; 2)

Do đó, hàm số đồng biến trên khoảng (-2; 0) và nghịch biến trên khoảng (0; 2).

b) \(y=\frac{x}{x^2+1}\)

Tập xác định của hàm số là R.

Ta có: \(y'=\frac{x^2+1-2x^2}{(x^2+1)^2}=\frac{1-x^2}{(x^2+1)^2}\)

y' = 0 \(\Leftrightarrow\) x = 1 hoặc x = - 1.

Lập bảng biến thiên của hàm số:

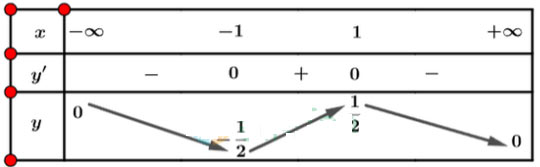
Từ bảng biến thiên, ta có:

Hàm số đồng biến trên khoảng (- 1; 1)

Hàm số nghịch biến trên khoảng (- ∞; - 1) và (1; + ∞).

Bài 1.5

a) Tính số dân của thị trấn đó vào các năm 2000 và 2015.

b) Tính đạo hàm N’(t) và \(\mathop {\lim }\limits_{t \to + \infty } N\left( t \right)\). Từ đó giải thích tại sao dân số của thị trấn đó luôn tăng nhưng sẽ không vượt qua một ngưỡng nào đó.

Lời giải:

a) Số dân của thị trấn đó vào năm 2000, tức t = 0 là:

\(N\left(0\right)=\frac{25.0+10}{0+5}=2\) (nghìn người)

Số dân của thị trấn đó vào năm 2015, tức t = 15 là:

\(N\left(15\right)=\frac{25.15+10}{15+5}=19,25\) (nghìn người)

b) Ta có \(N'\left(t\right)=\frac{25\left(t+5\right)-\left(25t+10\right)}{\left(t+5\right)^2}=\frac{115}{\left(t+5\right)^2} >0\) với mọi t.

\(\lim_{t\rightarrow +\infty} N(t) = \lim_{t\rightarrow +\infty} \frac{25t+10}{t+5}=25\)

Do đó số dân của thị trấn đó luôn tăng nhưng sẽ không vượt quá 25 nghìn người.

Bài 1.6

Đồ thị của đạo hàm bậc nhất \(y = f'\left( x \right)\) của hàm số f(x) được cho trong Hình 1.13:

a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích.

b) Tại giá trị nào của x thì f(x) có cực đại hoặc cực tiểu? Giải thích.

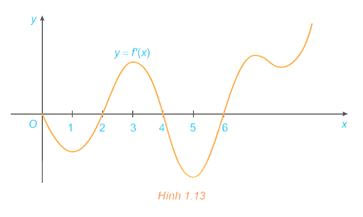
Lời giải:

a) Từ đồ thi của hàm số y = f'(x), ta có:

Hàm số đồng biến trên các khoảng (2; 4) và (6; + ∞)

Hàm số nghịch biến trên các khoảng (0; 2) và (4; 6)

b) Ta có:

f'(x) < 0 với mọi điểm x ∈ (0; 2) và f'(x) > 0 với mọi điểm x ∈ (0; 4) nên x = 2 là điểm cực tiểu.

f'(x) < 0 với mọi điểm x ∈ (4; 6) và f'(x) > 0 với mọi điểm x ∈ (6; + ∞) nên x = 6 là điểm cực tiểu.

f'(x) > 0 với mọi điểm x ∈ (2; 4) và f'(x) < 0 với mọi điểm x ∈ (4; 6) nên x = 4 là điểm cực đại.

Bài 1.7 

Tìm cực trị của các hàm số sau:

a) \(y = 2{x^3} - 9{x^2} + 12x - 5\);

b) \(y = {x^4} - 4{x^2} + 2\);

c) \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\);

d) \(y = \sqrt {4x - 2{x^2}}\).

Bài 1.8

Cho hàm số \(y = f\left( x \right) = \left| x \right|\).

a) Tính các giới hạn \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\) và \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}}\). Từ đó suy ra hàm số không có đạo hàm tại x = 0.

b) Sử dụng định nghĩa, chứng minh hàm số có cực tiểu tại x = 0. (Xem Hình 1.4)

Bài 1.9

Giả sử doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) tuân theo quy luật logistic được mô hình hóa bằng hàm số \(f\left( t \right) = \frac{{5\;000}}{{1 + 5{e^{ - t}}}},t \ge 0,\) trong đó thời gian t được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm f’(t) sẽ biểu thị tốc độ bán hàng. Hỏi sau khi phát hành bao nhiêu năm thì tốc độ bán hàng là lớn nhất?