Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Giải Toán 12 Kết nối tri thức trang 15 → 19

Giải Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số là tài liệu vô cùng hữu ích giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 12 Kết nối tri thức với cuộc sống tập 1 trang 15, 16, 17, 18, 19.

Giải bài tập Toán 12 Kết nối tri thức tập 1 Bài 2 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 2 Chương I: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số. Mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Giải Toán 12 Kết nối tri thức Tập 1 trang 19

Bài 1.10 

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) \(y = - {x^2} + 4x + 3\);

b) \(y = {x^3} - 2{x^2} + 1\) trên \(\left[ {0; + \infty } \right)\);

c) \(y = \frac{{{x^2} - 2x + 3}}{{x - 1}}\) trên \(\left( {1; + \infty } \right)\);

d) \(y = \sqrt {4x - 2{x^2}}\).

Hướng dẫn giải:

a) y = - x² + 4x + 3

Tập xác định của hàm số là: R

Ta có: y' = - 2x + 4; y' = 0 ⇔ x = 2

Lập bảng biến thiên của hàm số:

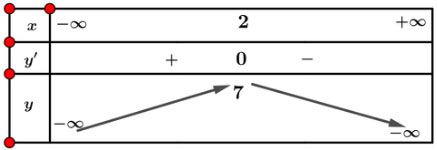
Từ bảng biến thiên ta được: \(\underset{\mathbb{R}}{\max} y = 7\), hàm số không có giá trị nhỏ nhất.

b) y = x³ - 2x² + 1 trên [0; + ∞)

Ta có: y' = 3x² - 4x = x(3x - 4)

y' = 0 ⇔ x = 0 hoặc x = \(\frac{4}{3}\) (vì x ∈ [0; + ∞))

Lập bảng biến thiên của hàm số trên [0; + ∞):

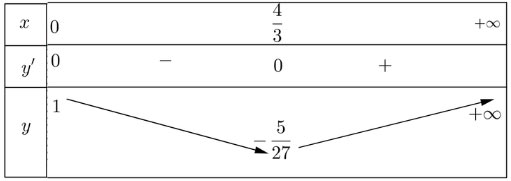
Từ bảng biến thiên, ta được: \(\underset{[0; + ∞)}{\min} y = - \frac{5}{27}\), hàm số không có giá trị lớn nhất.

c) \(y=\frac{x^2-2x+3}{x-1}\) trên (1; + ∞)

Ta có: \(y'=\frac{x^2-2x-1}{\left(x-1\right)^2}\)

y' = 0 ⇔ \(x=\sqrt{2}+1\) (vì x ∈ (1; + ∞))

Lập bảng biến thiên của hàm số trên (1; + ∞):

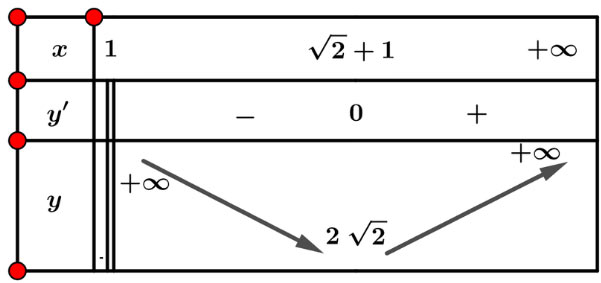
Từ bảng biến thiên, ta được: \(\underset{(1; + ∞)}{\min} y = 2\sqrt{2}\), hàm số không có giá trị lớn nhất.

d) \(y=\sqrt{4x-2x^2}\)

Bài 1.11

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) y = x⁴ – 2x² + 3;

b) y = xe^−x;

c) y = xlnx;

d) \(y = \sqrt{x - 1} + \sqrt{3 - x}\)

Hướng dẫn giải:

a) y = x⁴ - 2x² + 3

Tập xác định của hàm số là: R

Ta có: y' = 4x³ - 4x = 4x(x - 1)(x + 1)

y' = 0 ⇔ \(\left [ \begin{array}{l} x= - 1 \\ x = 0 \\ x = 1 \end{array} \right.\)

Lập bảng biến thiên của hàm số:

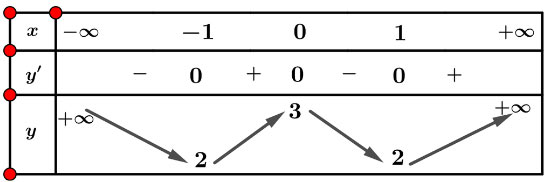
Từ bảng biến thiên ta được: \(\underset{\mathbb{R}}{\max} y = 3,\ \underset{\mathbb{R}}{\min} y = 2\).

b) y = xe^{- x}

Tập xác định của hàm số là: R

Ta có: \(y'=\frac{1-x}{e^x}\); y' = 0 ⇔ x = 1

Lập bảng biến thiên của hàm số:

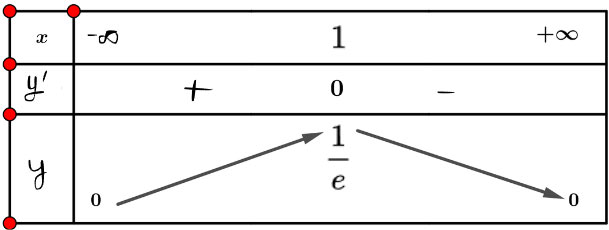
Từ bảng biến thiên, ta được: \(\underset{R}{\max} y = \frac{1}{e}\), hàm số không có giá trị nhỏ nhất.

c) \(y=x \ln x\)

Tập xác định của hàm số là: (0; + ∞)

Ta có: y' = ln x + 1; y' = 0 ⇔ \(x=\frac{1}{e}\)

Lập bảng biến thiên của hàm số trên (0; + ∞):

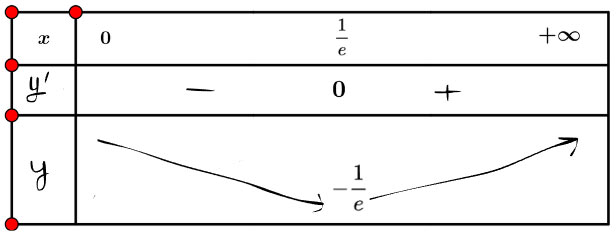
Từ bảng biến thiên, ta được: \(\underset{R}{\min} y = -\frac{1}{e}\), hàm số không có giá trị lớn nhất.

d) \(y=\sqrt{x-1} +\sqrt{3-x}\)

Tập xác định của hàm số là: [1; 3]

Ta có: \(y'=\frac{1}{2\sqrt{x-1}}+\frac{1}{2\sqrt{3-x}}\)

y' = 0 ⇔ x = 2

\(y\left(1\right)=\sqrt{2};\ y\left(2\right)=2;\ y\left(3\right)=\sqrt{2}\)

Từ bảng biến thiên, ta được: \(\underset{[1;3]}{\max} y = 2, \ \underset{[1;3]}{\min} y = \sqrt{2}\).

Bài 1.12

Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:

a) \(y = 2{x^3} - 6x + 3\) trên đoạn \(\left[ { - 1;2} \right]\);

b) \(y = {x^4} - 3{x^2} + 2\) trên đoạn \(\left[ {0;3} \right]\);

c) \(y = x - \sin 2x\) trên đoạn \(\left[ {0;\pi } \right]\);

d) \(y = \left( {{x^2} - x} \right){e^x}\) trên đoạn \(\left[ {0;1} \right]\).

Hướng dẫn giải:

Bài 1.13

Trong các hình chữ nhật có chu vi là 24cm, hãy tìm hình chữ nhật có diện tích lớn nhất.

Hướng dẫn giải:

Nửa chu vi: 24 : 2 = 12 cm

Gọi chiều dài là x (cm), chiều rộng là 12 - x (cm) (0 < x < 12)

Gọi S(x) là hàm số biểu thị diện tích của hình chữ nhật, ta có:

S(x) = x(12 - x) = 12x - x², 0 < x < 12

Ta có: S'(x) = 12 - 2x; S'(x) = 0 ⇔ x = 6

Lập bảng biến thiên của hàm số S(x) trên (0; 12):

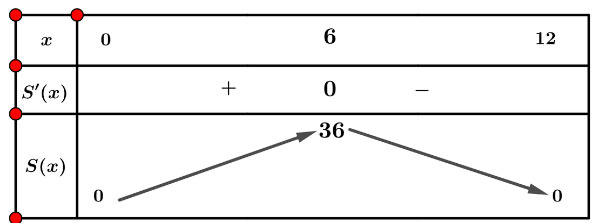
Từ bảng biến thiên, ta có \(\underset{(0;12)}{\max} S(x) = 36\)

Vậy hình chữ nhật có diện tích lớn nhất là 36 cm² (tức là khi chữ nhật trở thành hình vuông)

Bài 1.14

Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng 108cm² như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.

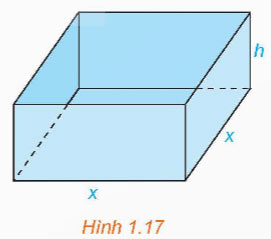
Hướng dẫn giải:

Diện tích bề mặt là: 4xh + x² = 108 (cm²)

⇒ \(h=\frac{108-x^2}{4x}\)

Gọi V(x) là hàm số biểu thị thể tích của hình hộp chữ nhật, ta có:

\(V(x)=S_{đáy}.h=\frac{x\left(108-x^2\right)}{4}=\frac{-x^3+108x}{4}\), x > 0

Ta có: \(V'\left(x\right)=-\frac{3x^2}{4}+27\); V'(x) = 0 ⇔ x = 6 (do x > 0)

Lập bảng biến thiên của hàm số V(x) trên (0; + ∞):

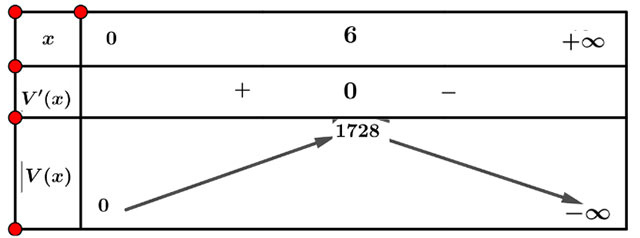
Từ bảng biến thiên, ta có \(\underset{(0;+ \infty )}{\max}V(x) = 1728\)

Vậy để hình hộp có thể tích lớn nhất thì đáy có cạnh bằng 6 và chiều cao h = 3 cm.

Bài 1.15

Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích 1000 cm³. Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,2 nghìn đồng/cm², trong khi mặt bên của bình được làm bằng vật liệu có giá 0,75 nghìn đồng/cm². Tính các kích thước của bình để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất.

Hướng dẫn giải:

Diện tích mặt đáy là: S_đáy = πR² (cm²)

Thể tích khối trụ là: V = πR²h = 1 000 (cm³) => Chiều cao khối trụ là: \(h=\frac{1\ 000}{\pi R^2}\) (cm)

Diện tích xung quanh khối trụ là: S_xq = 2πRh = \(\frac{2000}{R}\) (cm²)

Gọi C(R) là hàm số biểu thị chi phí vật liệu sản xuất mỗi chiếc bình, ta có:

\(C\left(R\right)=2\pi R^2.1,2+\frac{2000}{R}.0,75=2,4\pi R^2+\frac{1500}{R}\), R > 0

Ta có: \(C'\left(R\right)=4,8\pi R-\frac{1500}{R^2}\); C'(x) = 0 ⇔ \(R=\sqrt[3]{\frac{625}{2\pi}}\) (do R > 0)

Lập bảng biến thiên của hàm số C'(R) trên (0; + ∞):

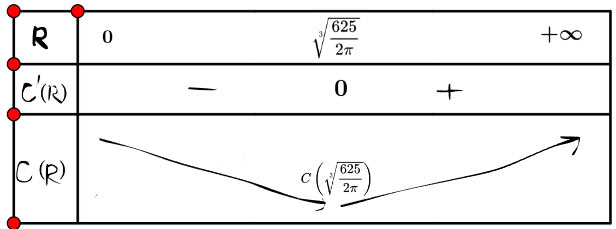
Vậy để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất thì bán kính đáy \(R=\sqrt[3]{\frac{625}{2\pi}}\)