Phân dạng và bài tập Hình học lớp 9 Các dạng toán hình lớp 9 và cách giải

Tổng hợp các dạng toán Hình học lớp 9 là nguồn tư liệu hữu ích mà các bạn học sinh lớp 9 không thể bỏ lỡ. Các dạng toán Hình học lớp 9 được biên soạn rất chi tiết kỹ lưỡng gồm 71 trang tổng hợp toàn bộ các bài tập trọng tâm.

Các dạng Toán hình lớp 9 tổng hợp toàn bộ kiến thức về lý thuyết, ví dụ minh họa, các dạng bài tập có đáp án giải chi tiết kèm theo tự luyện. Qua đó giúp các bạn học sinh tham khảo, hệ thống lại kiến thức để giải nhanh các bài tập hình học 9. Ngoài ra để nâng cao kiến thức môn Toán thật tốt các em xem thêm một số tài liệu như: chuyên đề Giải phương trình bậc 2 chứa tham số, bài tập hệ thức Vi-et và các ứng dụng. Nội dung tài liệu các dạng Toán hình lớp 9 bao gồm:

Chương 1: Hệ thức lượng trong tam giác vuông

Chủ đề 1. Hệ thức về cạnh và đường cao trong tam giác vuông

• Dạng 1. Tính độ dài đoạn thẳng trong tam giác vuông.
• Dạng 2. Dựng đoạn thẳng Py-ta-go; Dựng đoạn trung bình nhân.
• Dạng 3. Chứng minh hệ thức hình học.

Chủ đề 2. Tỉ số lượng giác của một góc nhọn

• Dạng 1. Tính tỉ số lượng giác.
• Dạng 2. Dựng góc α biết một tỉ số lượng giác là m/n.
• Dạng 3. Tính cạnh, tỉ số lượng giác của góc còn lại khi biết tỉ số lượng giác của một góc.
• Dạng 4. Sắp thứ tự các tỉ số lượng giác mà không dùng bảng số và máy tính.
• Dạng 5. Chứng minh hệ thức lượng giác.

Chủ đề 3. Hệ thức về cạnh và góc trong tam giác vuông

• Dạng 1. Giải tam giác vuông biết độ dài một cạnh và số đo một góc nhọn.
• Dạng 2. Giải tam giác vuông biết hai cạnh.
• Dạng 3. Tính cạnh, tính góc của tam giác.

Chương 2. Đường tròn

Chủ đề 1. Sự xác định đường tròn

• Dạng 1. Chứng minh nhiều điểm cùng thuộc một đường tròn.
• Dạng 2. Xác định tâm và bán kính của đường tròn ngoại tiếp.
• Dạng 3. Dựng đường tròn thỏa mãn điều kiện cho trước.

Chủ đề 2. Đường kính và dây cung của một cung tròn

• Dạng 1. Chứng minh hai đoạn thẳng bằng nhau. Hai dây bằng nhau.
• Dạng 2. Tính độ dài một đoạn thẳng. Độ dài một cung.
• Dạng 3. So sánh hai dây cung – Hai đoạn thẳng.

Chủ đề 3. Vị trí tương đối của đường thẳng và đường tròn

• Dạng 1. Xác định vị trí tương đối của đường thẳng và đường tròn.
• Dạng 2. Tìm vị trí tâm của một đường tròn có bán kính cho trước tiếp xúc với một đường thẳng cho trước.

Chủ đề 4. Các tính chất của tiếp tuyến

• Dạng 1. Tính độ dài của một đoạn tiếp tuyến.
• Dạng 2. Chứng minh một đường thẳng là tiếp tuyến của một đường tròn.
• Dạng 3. Chứng minh đẳng thức hình học.

Chủ đề 5. Vị trí tương đối của hai đường tròn

• Dạng 1. Xác định vị trí tương đối của hai đường tròn.
• Dạng 2. Các bài toán với hai đường tròn tiếp xúc nhau.
• Dạng 3. Các bài toán với hai đường tròn cắt nhau.

Chương 3: Góc với đường tròn

Chủ đề 1. Góc ở tâm, số đo cung, liên hệ giữa cung và dây.

• Dạng 1. Sự liên hệ giữa góc ở tâm và cung.
• Dạng 2. Sự liên hệ giữa cung và dây.

Chủ đề 2. góc nội tiếp và góc tạo bởi tia tiếp tuyến với một dây cung

• Dạng 2. Góc tạo bởi tia tiếp tuyến và dây cung.

Chủ đề 3. Góc có đỉnh ở trong hoặc ngoài đường tròn

Dạng 1. Áp dụng góc có đỉnh ở trong đường tròn.

Chủ đề 4. Cung chứa góc

Dạng 1. Áp dụng giải các bài toán về quỹ tích và dựng hình.

Chủ đề 5. Tứ giác nội tiếp và đường tròn ngoại tiếp

• Dạng 1. Chứng minh tứ giác nội tiếp.
• Dạng 2. Chứng minh nhiều điểm cùng nằm trên một đường tròn.

Chủ đề 6. Tứ giác ngoại tiếp và đường tròn ngoại tiếp

• Dạng 1. Chứng minh các hệ thức liên hệ giữa các cạnh của tứ giác ngoại tiếp.
• Dạng 2. Chứng minh tứ giác ngoại tiếp.

Chủ đề 7. Độ dài đường tròn và độ dài cung tròn

• Dạng 1. Tính độ dài đường tròn, cung tròn hoặc các đại lượng liên quan.
• Dạng 2. Tính độ dài của cung tròn do các cung chắp nối thành.

Chủ đề 8. Diện tích hình tròn, diện tích hình quạt

• Dạng 1. Tính diện tích hình tròn, quạt tròn.
• Dạng 2. Tính diện tích hình viên phân, hình vành khăn và những hình khác có liên quan đến cung tròn.

Chương 4: Hình trụ - hình nón - hình cầu

Chủ đề 1. Diện tích xung quanh và thể tích hình trụ

• Dạng 1. Tính diện tích xung quanh – Diện tích toàn phần, thể tích hình trụ hoặc các yếu tố liên quan.
• Dạng 2. Diện tích xung quanh – Thể tích của một hình hỗn hợp.

Chủ đề 2. Diện tích xung quanh và thể tích của hình nón, hình nón cụt

• Dạng 1. Tính số đo cung hoặc bán kính hình quạt tròn hoặc nửa góc ở đỉnh của hình nón.
• Dạng 2. Diện tích xung quanh, thể tích của hình nón, nón cụt và các đại lượng có liên quan nếu biết hai trong ba yếu tố. Bán kính đáy, chiều cao, đường sinh.
• Dạng 3. Tính diện tích xung quanh, thể tích của một hình hỗn hợp, gồm nhiều hình.

Chủ đề 3. Diện tích mặt cầu và thể tích hình cầu

• Dạng 1. Tính diện tích mặt cầu, thể tích hình cầu khi biết bán kính của hình cầu hoặc ngược lại, tính bán kính hình cầu khi biết thể tích hoặc diện tích của nó.
• Dạng 2. Tính diện tích, thể tích của một hình hỗn hợp gồm nhiều hình.

..........

Các dạng Toán hình lớp 9 và cách giải

Chương 1: Hệ thức lượng trong tam giác vuông

A. Kiến thức trọng tâm 

Cho tam giác ABC vuông tại A, cạnh huyền BC = a, các cạnh góc vuông AC = b và AB = c. Gọi AH = h là đường cao ứng với cạnh huyền CH = b', BH = c' lần lượt là hình chiếu của AC, AB trên cạnh huyền BC.

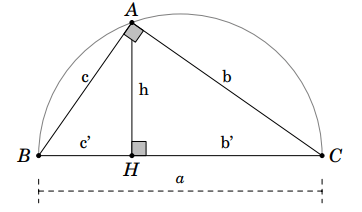
1. Ba hệ thức về cạnh

1, c² = ac',

2. b² = ab'

3, a² = b² + c²

2. Ba hệ thức về đường cao

1. ah = bc

2., h² = b'.c'

3. 1/h² = 1/b₂ + 1/c₂

3. Dấu hiệu nhận biết tam giác vuông

• Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng một nữa cạnh ấy thì
  tam giác đó là tam giác vuông.
• Dấu hiệu này sinh ra cách vẽ một tam giác vuông bằng thước kẻ và compa gồm hai
  bước:

B1: Vẽ một nữa đường tròn tâm O, đường kính BC.

B2: Lấy điểm A bất kì trên nữa đường tròn thu được tam giác ABC vuông tại A.  

B. Các dạng bài tập cơ bản 

- Tính độ dài đoạn thẳng trong tam giác vuông

Xác định vị trí cạnh huyền.

Áp dụng hệ thức về cạnh hoặc đường cao.

- Tính độ dài đoạn thẳng trong tam giác vuông

• Xác định vị trí cạnh huyền.
• Áp dụng hệ thức về cạnh hoặc đường cao.

Ví dụ 1.

Hãy tính x, y với các kích thước như hình bên.

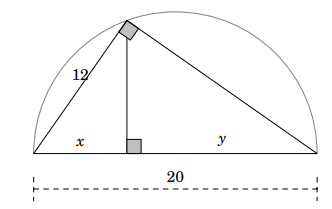
Ví dụ 2.

Hãy tính x, y với các kích thước như hình bên.

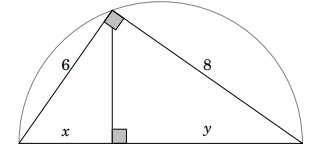
Ví dụ 3.

Hãy tính x, y với các kích thước như hình bên.

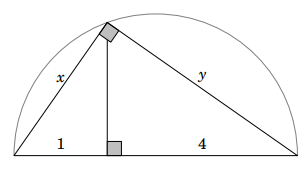
Ví dụ 4 

Hãy tính x, y với các kích thước như hình bên.

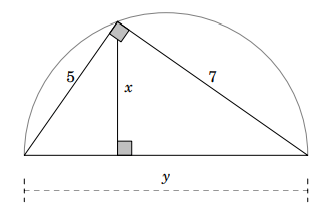
Ví dụ 5.

Hãy tính x, y với các kích thước như hình bên.

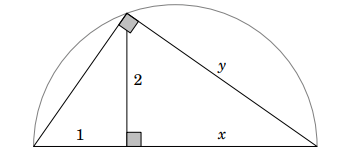
4. Bài tập vận dụng

Bài 1. Cho tam giác ABC có góc A = 90 độ , AB = 12cm, BC = 13cm. Tính AC, đường cao AH, các đoạn thẳng BH, CH và diện tích của tam giác.

Bài 2. Cho 4ABC vuông cạnh huyền AB, cạnh AC = 15, đường cao CH chia AB thành hai đoạn AH và HB với HB = 16. Tính diện tích tam giác ABC.

Bài 3. Cho tam giác ABC cân tại A có cạnh bên bằng 15cm, cạnh đáy bằng 18 cm. Tính độ dài các đường cao.

Bài 4. Tính diện tích của một tam giác cân có chiều cao ứng với cạnh đáy bằng 10cm, chiều cao ứng với với cạnh bên bằng 12cm.

Bài 5. Cho tam giác ABC vuông tại A, đường phân giác trong BE, biết EC = 3, BC = 6. Tính độ dài các đoạn thẳng AB, AC.

Bài 6. Tính diện tích tam giác có độ dài ba cạnh là 10cm, 17cm, 21cm

Dạng 2: Dựng đoạn thẳng Py-ta-go; Dựng đoạn trung bình nhân

1. Dựng đoạn thẳng Py-ta-go \(a^2+b^2\)

Loại 1. Cho trước hai đoạn thẳng a và b. 

Dựng tam giác vuông có 2 cạnh góc vuông là a và b thì cạnh huyền bằng x

 Loại 2. Cho trước hai đoạn thẳng a và b. Dựng đoạn thẳng

\(y=\sqrt{x^2-b^2}(x>b)=y^2+b^2 = a^2 .\)

Dựng tam giác vuông có cạnh huyền là a, cạnh góc vuông là b thì cạnh góc vuông
kia là y. 

2. Dựng đoạn trung bình nhân

Cho trước hai đoạn thẳng a và b. Dựng đoạn thẳng \(x=\sqrt{ah}\)

Dựng tam giác ABC có cạnh huyền BC = a + b có góc A bằng 90 độ thì đường cao ứng với cạnh huyền là x với BH = a, HC = b.

Ví dụ 1. Dựng đoạn thẳng \(\sqrt{2}\) bằng cách dựng đoạn thẳng Py-ta-go.

Ví dụ 2. Dựng đoạn thẳng \(\sqrt{5}\) bằng cách dựng đoạn thẳng Py-ta-go.

Ví dụ 3. Dựng đoạn thẳng \(\sqrt{5}\) bằng cách dựng đoạn thẳng Py-ta-go.

Ví dụ 4. Dựng đoạn thẳng \(\sqrt{3}\) bằng cách dựng đoạn thẳng Py-ta-go.

Ví dụ 5. Dựng đoạn thẳng \(\sqrt{3}\) bằng cách dựng trung bình nhân.

Ví dụ 6. Dựng đoạn thẳng \(\sqrt{5}\) bằng cách dựng đoạn trung bình nhân.

BÀI TẬP VẬN DỤNG

Bài 1. Dựng đoạn thẳng \(\sqrt{7}\) bằng cách dựng đoạn thẳng Py-ta-go.

Bài 2. Dựng đoạn thẳng \(\sqrt{6}\) bằng cách dựng trung bình nhân.

Dạng 3: Chứng minh hệ thức hình học

1. Chọn các tam giác vuông thích hợp chứa các đoạn thẳng có trong hệ thức. Tính các
đoạn thẳng đó nhờ các hệ thức về cạnh và đường cao.

2. Liên kết các giá trị trên rút ra hệ thức phải chứng minh.

VÍ DỤ MINH HỌA

Ví dụ 1. Cho tam giác ABC vuông tại A, đường cao AH. Gọi M, N lần lượt là hình chiếu vuông
góc của H trên AB và AC. Chứng minh rằng:

\(a) A M \cdot A B=A N \cdot A C;\)

\(b) H B \cdot R C=M A \cdot M \bar{B}+N A \cdot N C;\)

\(e) \frac{A B}{H C}-\left(\frac{A B}{A C}\right)^2\)

.........