Các định lý Hình học nổi tiếng ôn thi vào lớp 10 Các định lý Hình học lớp 9

Các định lý Hình học lớp 9 là tài liệu vô cùng hữu ích được biên soạn đầy đủ và chi tiết nhất về 20 định lí trọng tâm thường có trong đề thi vào 10 môn Toán.

TOP 20 Định lý Hình học lớp 9 được trình bày rất bài bản các vấn đề quan trọng nhất cần ghi nhớ, ví dụ minh họa kèm theo các dạng bài tập giải chi tiết. Qua đó giúp học sinh nhanh chóng đối chiếu so sánh với bài làm của mình tự nhận xét được năng lực bản thân, thấy được lỗi sai cần tránh, kịp thời lấp đầy lỗ hổng kiến thức, tìm ra các phương pháp làm bài nhanh. Nội dung tài liệu bao gồm các định lý sau:

• Đường thẳng Euler.
• Đường thẳng Simmon.
• Đường thẳng Steiner.
• Đường tròn Euler.
• Điểm Miquel.
• Đường tròn Miquel.
• Định lý Miquel.
• Định lý Lyness.
• Định lý Lyness mở rộng (bổ đề Sawayama).
• Một hệ quả của định lý Lyness mở rộng.
• Định lý Ptolemy cho tứ giác nội tiếp.
• Định lý Ptolemy cho tứ giác bất kỳ.
• Định lý Brocard.
• Định lý con bướm với đường tròn.
• Định lý con bướm mở rộng với đường tròn.
• Định lý con bướm với cặp đường thẳng.
• Định lý Shooten.
• Hệ thức Van Aubel.
• Định lý Ce’va.
• Định lý Menelaus.

Các định lý Hình học lớp 9

1. Đường thẳng Euler

1.(Đường thẳng Euler). Cho tam giác ABC. Chứng minh rằng trọng tâm G, trực tâm H và tâm đường tròn ngoại tiếp O cùng nằm trên một đường thẳng. Hơn nữa \(\frac{GH}{GO}=2\). Đường thẳng H, G, O nối gọi là đường thẳng Euler của tam giác ABC.

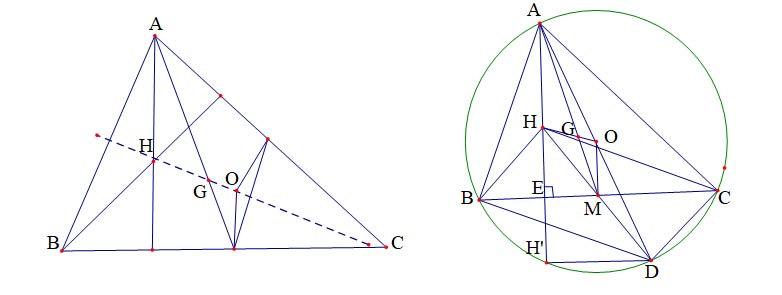
Cách 1: Gọi E, F lần lượt là trung điểm của BC, AC. Ta có EF là đường trung bình của tam giác A B C nên EF / / AB. Ta lại có OF / / BH (cùng vuông góc với A C ). Do đó \(\overline{O F E}=\bar{A} B H\) (góc có canh tương ứng song song). Chứng minh tương tư \(\overline{O E F}=\bar{B} A H.\)

Từ đó có \(\mathrm{D} A B H: \mathrm{D} E F O\) (g.g)\(\mathrm{p} \frac{A H}{O E}=\frac{A B}{E F}=2\) (do EF là đường trung bình của tam giác ABC ). Mặt khác G là trong tâm của tam giác ABC nên \(\frac{A G}{G E}=2\). Do đó \(\frac{A G}{F G}=\frac{A H}{O E}=2\), lai có \(\bar{H} A G=\bar{O} E G\) (so le trong, OE / / AH ) \(\mathrm{D}\) DHAG: \(\mathrm{D} E O G (c.g.c) \mathrm{p} \quad \bar{H} G A=\bar{E} G O\). Do \(\bar{E} G O+\bar{A} G O=180^{\circ} nên \bar{H} G A+\bar{A} G O=180^{\circ} hay \bar{H} G O=180^{\circ} .\)

Vây H, G, O thẳng hàng.

Cách 2: Kẻ đường kính AD của đường tròn (O) ta có \(B H \wedge A C\) (Tính chất trực tâm) \(\mathrm{AC}^{\wedge} \mathrm{CD}\)(Góc nội tiếp chắn nửa đường tròn) suy ra BH / / CD. Tương tự ta cũng có CH / / BD nên tứ giác BHCD là hình bình hành, do đó HD cắt BC tại trung điểm của mỗi đường. Từ đó cũng suy ra \(O M / /=\frac{1}{2} A H\) (Tính chất đường trung bình tam giác ADH ). Nối AM cắt HO tai G thì \(\frac{G O}{G H}=\frac{O M}{A H}=\frac{1}{2}\) nên G là trọng tâm của tam giác ABC .

Chú ý rằng: Nếu ta kéo dài AH cắt đường tròn tai \(\mathrm{H}^{\prime}\) thì \(\widehat{\mathrm{AH}} \mathrm{D}=90^{0}\) (Góc nội tiếp chắn nửa đường tròn) nên EM là đường trung bình của tam giác HH'D suy ra H đối xứng với H' qua BC. Nếu gọi O là tâm vòng tròn ngoại tiếp tam giác HBC thì ta có \(\mathrm{O}^{\prime}\) đối xứng với O qua BC.

Đường thẳng đi qua H, G, O được gọi là đường thẳng Euler của tam giác ABC. Ngoài ra ta còn có OH=3 OG.

*Đường thẳng Euler có thể coi là một trong những định lý quen thuộc nhất của hình học phẳng. Khái niệm đường thẳng Euler trước hết liên quan đến tam giác, sau đó được mở rộng và ứng dụng cho tứ giác nội tiếp và cả n - giác nội tiếp, trong chuyên đề ta quan tâm đến một số vấn đề có liên quan đến khái niệm này trong tam giác.

.............

Nội dung chi tiết tài liệu các định lý hình học 9