Toán 11 Bài 1: Giá trị lượng giác của góc lượng giác Giải Toán 11 Kết nối tri thức trang 5, 6, 7, 8, ... 16

Giải Toán 11 Kết nối tri thức Tập 1 trang 16 giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi hoạt động và 6 bài tập trong SGK bài Giá trị lượng giác của góc lượng giác được nhanh chóng và dễ dàng hơn.

Toán 11 Kết nối tri thức trang 16 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh lớp 11 học tốt môn Toán 11. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 11 Kết nối tri thức Tập 1 trang 16 mời các bạn cùng theo dõi.

Hoạt động Toán 11 Kết nối tri thức tập 1

Hoạt động 1

Trên đồng hồ ở Hình 1.2, kim phút đang chỉ đúng số 2.

a) Phải quay kim phút mấy phần của một vòng tròn theo chiều quay ngược chiều kim đồng hồ để nó chỉ đúng số 12?

b) Phải quay kim phút mấy phần của một vòng tròn theo chiều quay của kim đồng hồ để nó chỉ đúng số 12?

c) Có bao nhiêu cách quay kim phút theo một chiều xác định để kim phút từ vị trí chỉ đúng số 2 về vị trí chỉ đúng số 12?

Gợi ý đáp án 

a) Theo chiều quay ngược chiều kim đồng hồ, để kim phút chỉ đúng số 12 thì kim phút quay được: \(\frac{2}{12}=\frac{1}{6}\) phần của một vòng tròn

b) Theo chiều quay cùng chiều kim đồng hồ, để kim phút chỉ đúng số 12 thì kim phút quay được: \(\frac{10}{12}=\frac{5}{6}\) phần của một vòng tròn

c) Có 2 cách quay kim phút theo một chiều xác định để kim phút từ vị trí chỉ đúng số 2 về vị trí chỉ đúng số 12: ngược chiều kim đồng hồ và cùng chiều kim đồng hồ

Hoạt động 2

Cho ba tia Ou, Ov, Ow với số đo của các góc hình học uOv và vOw lần lượt là 30⁰ và 45⁰.

a) Xác định số đo của ba góc lượng giác (Ou,Ov), (Ov,Ow) và (Ou, Ow) được chỉ ra ở Hình 1.5

b) Với các góc lượng giác ở câu a, chứng tỏ rằng có một số nguyên k để sđ(Ou,Ov) + sđ(Ov,Ow) = sđ(Ou,Ow) + k360^o (k ∊ Z)

Gợi ý đáp án 

a) Góc lượng giác có tia đầu Ou, tia cuối Ov, theo chiều quay ngược chiều kim đồng hồ:

sđ(Ou, Ov) = 30^o + k360^o (k ∊ Z)

Góc lượng giác có tia đầu Ov, tia cuối Ow, theo chiều quay ngược chiều kim đồng hồ:

sđ(Ov, Ow) = 45^o + k360^o (k ∊ Z)

Góc lượng giác có tia đầu Ou, tia cuối Ow, theo chiều quay cùng chiều kim đồng hồ:

sđ(Ou, Ow) = 75^o + k360^o (k ∊ Z)

b) Với các góc lượng giác ở câu a, ta có:

sđ(Ou, Ov) + sđ(Ov, Ow)

= 30^o + k360^o + 45^o + k360^o

= sđ(Ou, Ow) + k360^o (k ∊ Z)

Vậy với một số nguyên k, ta có sđ(Ou,Ov) + sđ(Ov,Ow) = sđ(Ou,Ow) + k360^o (k ∊ Z)

Hoạt động 3

Cho đường tròn bán kính R

a) Độ dài của cung tròn có số đo bằng 1 rad là bao nhiêu?

b) Tính độ dài l của cung tròn có số đo α rad

Gợi ý đáp án

a) Độ dài của cung tròn có số đo bằng 1 rad là bằng bán kính R.

b) Độ dài l của cung tròn có số đo α là \(l=Rα\)

Phần Bài tập Toán 11 Kết nối tri thức tập 1 trang 16

Bài 1.1 SGK Toán 11 Kết nối tri thức

Hoàn thành bảng sau

Gợi ý đáp án:

Bài 1.2 SGK Toán 11 Kết nối tri thức

Một đường tròn có bán kính 20 cm. Tìm độ dài của các cung trên đường tròn đó có số đo sau:

a) \(\frac{\pi }{12}\)

b) 1.5

c) \(35^{\circ}\)

d) \(315^{\circ}\)

Gợi ý đáp án:

a) Độ dài cung đường tròn: \(l=20\times \frac{\pi }{12}=5.236\) (cm)

b) Độ dài cung đường tròn: \(l=20\times 1.5=30\) (cm)

c) Đổi \(35^{\circ}=\frac{7\pi }{36}\)

Độ dài cung đường tròn: \(l=20\times \frac{7\pi }{36}=12.2173\) (cm)

d) Đổi \(315^{\circ}=\frac{7\pi }{4}\)

Độ dài cung đường tròn: \(l=20\times \frac{7\pi }{4}=109.9557\) (cm)

Bài 1.3 SGK Toán 11 Kết nối tri thức

Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau:

a) \(\frac{2\pi }{3}\)

b) \(-\frac{11\pi }{4}\)

c) \(150^{\circ}\)

d) \(315^{\circ}\)

Gợi ý đáp án

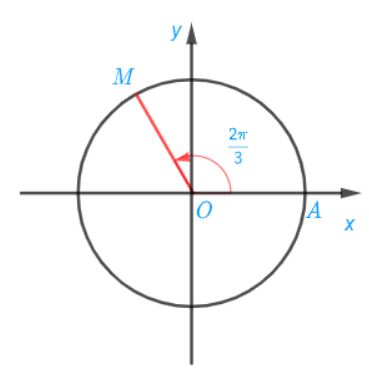
a) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng \(\frac{2\pi }{3}\) được xác định trong hình sau:

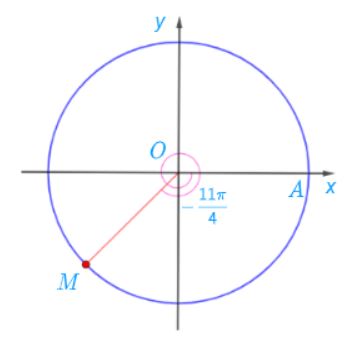
b) Ta có: \(-\frac{11\pi }{4}=-(\frac{3\pi }{4}+2\pi )\)

Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng \(-\frac{11\pi }{4}\) được xác định trong hình sau:

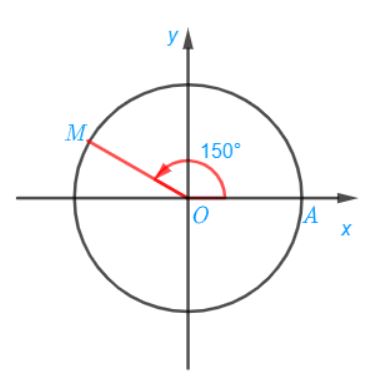
c) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng 150° được xác định trong hình sau:

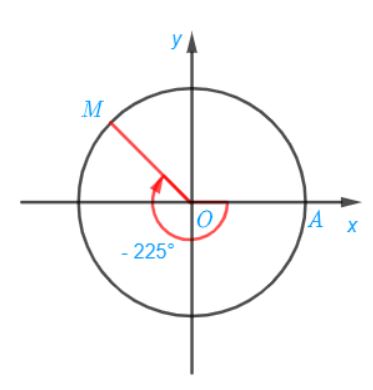
d) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng – 225° được xác định trong hình sau:

Bài 1.4 SGK Toán 11 Kết nối tri thức

Tính các giá trị lượng giác góc \(\alpha\), biết

a) \(cos\alpha =\frac{1}{5} và 0<\alpha <\frac{\pi }{2}\)

b) \(sin\alpha =\frac{2}{3} và \frac{\pi }{2}<\alpha <\pi\)

c) \(tan\alpha =\sqrt{5} và \pi < \alpha <\frac{3\pi }{2}\)

d) \(cot\alpha =-\frac{1}{\sqrt{2}} và \frac{3\pi }{2}<\alpha <2\pi\)

Gợi ý đáp án

a) Vì \(0 < \alpha <\frac{\pi }{2}\) nên \(sin \alpha > 0\)

Mặt khác, từ \(sin^{2}\alpha +cos^{2}\alpha =1\) suy ra \(sin\alpha =\sqrt{1-cos^{2}\alpha }=\sqrt{1-\frac{1}{25}}=\frac{2\sqrt{6}}{5}\)

Do đó, \(tan\alpha =\frac{sin\alpha }{cos\alpha }=\frac{\frac{2\sqrt{6}}{5}}{\frac{1}{5}}=2\sqrt{6}\) và \(cot\alpha =\frac{1}{tan\alpha }=\frac{1}{2\sqrt{6}}\)

b) Vì \(\frac{\pi }{2}<\alpha <\pi\) nên \(cos\alpha<0\)

Mặt khác, từ \(sin^{2}\alpha +cos^{2}\alpha =1 suy ra cos\alpha =-\sqrt{1-sin^{2}\alpha }=-\sqrt{1-\frac{4}{9}}=-\frac{\sqrt{5}}{3}\)

Do đó, \(tan\alpha =\frac{sin\alpha }{cos\alpha }=\frac{\frac{2}{3}}{-\frac{\sqrt{5}}{3}}=-\frac{2\sqrt{5}}{5} và cot\alpha =\frac{1}{tan\alpha }=\frac{-\sqrt{5}}{2}\)

c) \(cot\alpha =\frac{1}{tan\alpha }=\frac{1}{2-\sqrt{5}}\)

Vì \(\pi < \alpha <\frac{3\pi }{2}\) nên \(cos\alpha <0,sin\alpha <0\)

Mặt khác, từ \(1+tan^{2}\alpha =\frac{1}{cos^{2}\alpha }\) suy ra \(cos\alpha =-\sqrt{\frac{1}{1+tan^{2}\alpha }}=-\sqrt{\frac{1}{1+5}}=-\frac{1}{\sqrt{6}}\)

Từ \(1+cot^{2}\alpha =\frac{1}{sin^{2}\alpha }\) suy ra \(sin\alpha =-\sqrt{\frac{1}{1+cot^{2}\alpha }}=-\sqrt{\frac{1}{1+\frac{1}{5}}}=-\frac{\sqrt{30}}{6}\)

d) \(tan\alpha =\frac{1}{cot\alpha }=-\sqrt{2}\)

Vì \(\frac{3\pi }{2}<\alpha <2\pi\) nên \(cos\alpha >0,sin\alpha <0\)

Mặt khác, từ \(1+tan^{2}\alpha =\frac{1}{cos^{2}\alpha }\) suy ra \(cos\alpha =\sqrt{\frac{1}{1+tan^{2}\alpha }}=\sqrt{\frac{1}{1+2}}=\frac{1}{\sqrt{3}}\)

Từ \(1+cot^{2}\alpha =\frac{1}{sin^{2}\alpha }\) suy ra \(sin\alpha =-\sqrt{\frac{1}{1+cot^{2}\alpha }}=-\sqrt{\frac{1}{1+\frac{1}{2}}}=-\frac{\sqrt{6}}{3}\)

Bài 1.5 SGK Toán 11 Kết nối tri thức

Chứng minh các đẳng thức:

a) \(cos^{4}\alpha -sin^{4}\alpha =2cos^{2}\alpha -1\)

b) \(\frac{cos^{2}\alpha +tan^{2}\alpha -1}{sin^{2}\alpha }=tan^{2}\alpha\)

Gợi ý đáp án

a) \(cos^{4}\alpha -sin^{4}\alpha =(cos^{2}\alpha +sin^{2}\alpha )(cos^{2}\alpha -sin^{2}\alpha )\)

\(=1\times (cos^{2}\alpha -sin^{2}\alpha )=cos^{2}\alpha -(1-sin^{2}\alpha )=2cos^{2}\alpha -1\)

b) \(\frac{cos^{2}\alpha +tan^{2}\alpha -1}{sin^{2}\alpha }=\frac{cos^{2}\alpha }{sin^{2}\alpha }+\frac{tan^{2}\alpha }{sin^{2}\alpha }-\frac{1}{sin^{2}\alpha }\)

\(=cot^{2}\alpha +\frac{\frac{sin^{2}\alpha }{cos^{2}\alpha }}{sin^{2}\alpha }-(1+cot^{2}\alpha )=\frac{1}{cos^{2}}-1=tan^{2}\alpha\)

Bài 1.6 SGK Toán 11 Kết nối tri thức

Bánh xe của người đi xe đạp quay được 11 vòng trong 5 giây

a) Tính góc (theo độ và radian) mà bánh xe quay được trong 1 giây

b) Tính độ dài quãng đường mà người đi xe đã đi được trong 1 phút, biết rằng đường kính của bánh xe đạp là 680mm

Gợi ý đáp án

a) 1 giây bánh xe quay được số vòng là: \(11:5=\frac{11}{5}\) (vòng)

Góc mà bánh xe quay được trong 1 giây: \(\frac{11}{5}\times 360^{\circ}=792^{\circ}=4.4\pi\) (rad)

b) Ta có: 1 phút = 60 giây.

Trong 1 phút bánh xe quay được \(60\times \frac{11}{5}=132\) vòng.

Chu vi của bánh xe đạp là: C = 680π (mm).

Quãng đường mà người đi xe đạp đã đi được trong một phút là

\(680π\times 132 = 89 760π (mm) = 89,76π (m).\)

Luyện tập Giá trị lượng giác của góc lượng giác