Vật lí 11 Bài 7: Bài tập về sự chuyển hóa năng lượng trong dao động điều hòa Giải Lý 11 Kết nối tri thức trang 28, 29, 30

Bài trước

Mục lục

Bài sau

Giải Vật lý 11 trang 28, 29, 30 Kết nối tri thức với cuộc sống giúp các em học sinh lớp 11 có thêm nhiều gợi ý tham khảo để biết cách trả lời các câu hỏi bài học bài 7: Bài tập về sự chuyển hóa năng lượng trong dao động điều hòa của Chương 1: Dao động

Giải Lý 11 Kết nối tri thức bài 7 các em sẽ hiểu được kiến thức lý thuyết về động năng, thế năng, dao động tắt dần, ... biết cách trả lời toàn bộ các câu hỏi 1, 2, 3, 4 trang 28→30 trong sách giáo khoa Vật lí 11. Đồng thời qua đó giúp quý thầy cô tham khảo để soạn giáo án cho học sinh của mình.

Vật lí 11 Bài 7: Bài tập về sự chuyển hóa năng lượng trong dao động điều hòa

Bài tập về sự chuyển hóa năng lượng trong dao động điều hòa

Bài tập về sự chuyển hóa năng lượng trong dao động điều hòa

Bài 1 trang 29

Hình 7.3 mô tả một máy đo địa chấn đơn giản hoạt động theo nguyên tắc sau đây: Khi xảy ra động đất thì hệ gồm lò xo và vật nặng của máy đo sẽ dao động theo tần số của địa chấn. Bút dạ gắn với vật nặng sẽ ghi lại đồ thị của địa chấn trên cuộn giấy quay đều. Biết sóng địa chấn có tần số nằm trong khoảng từ 30 Hz đến 40 Hz.

Hãy giải thích tại sao tần số riêng của hệ (vật nặng + lò xo) trong máy địa chấn phải có giá trị nhỏ hơn tần số nay rất nhiều.

Gợi ý đáp án

Tần số riêng của hệ (vật nặng + lò xo) trong máy địa chấn phải có giá trị nhỏ hơn tần số sóng địa chấn vì để tránh xảy ra hiện tượng cộng hưởng dao động gây hỏng máy không đo được tần số của sóng địa chấn.

Bài 2 trang 29

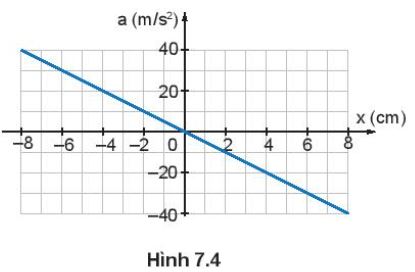
Đồ thị Hình 7.4 mô tả mối liên hệ giữa gia tốc và li độ của một vật dao động điều hoà.
Sử dụng số liệu trong đồ thị Hình 7.4 để tính tần số của dao động.

Gợi ý đáp án

Ta có: x = -0,04 (m) thì a = 20 ( m/s² )

$\Rightarrow a=-\omega ^{2}x \Leftrightarrow a=-(2\pi f)^{2}x \Leftrightarrow 20=(2\pi f)^{2}.0,04 \Leftrightarrow f=\frac{5\sqrt{5}}{2\pi}$ $\Rightarrow a=-\omega ^{2}x \Leftrightarrow a=-(2\pi f)^{2}x \Leftrightarrow 20=(2\pi f)^{2}.0,04 \Leftrightarrow f=\frac{5\sqrt{5}}{2\pi}$ (Hz)

Bài 3 trang 30

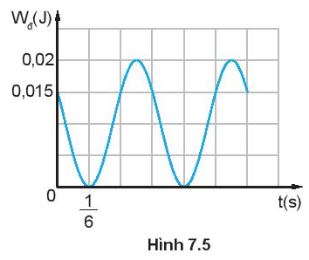
Hình 7.5 là đồ thị động năng theo thời gian của một vật khối lượng 0,4 kg dao động điều hoà. Tại thời điểm ban đầu vật đang chuyển động theo chiều dương, lấy $\pi ^{2}$ $\pi ^{2}$ = 10. Viết phương trình dao động của vật.

Gợi ý đáp án

Từ đồ thị ta có:

Tại thời điểm ban đầu t = 0: $Wđ = 0,015 J \Rightarrow W_{t}=0,02 - 0,015=0,005 (J)\Leftrightarrow W_{t}=\frac{W}{4}\Rightarrow x_{0}=\pm \frac{A}{2}$ $Wđ = 0,015 J \Rightarrow W_{t}=0,02 - 0,015=0,005 (J)\Leftrightarrow W_{t}=\frac{W}{4}\Rightarrow x_{0}=\pm \frac{A}{2}$

Tại thời điểm $t1 = \frac{1}{6} : Wđ = 0 \Rightarrow x_{1}=\pm A$ $t1 = \frac{1}{6} : Wđ = 0 \Rightarrow x_{1}=\pm A$

Dựa vào đồ thị ta suy ra: $x_{0}=\frac{A}{2}; x_{1}= A$ $x_{0}=\frac{A}{2}; x_{1}= A$

Khoảng thời gian từ x0 đến x1 là: $\Delta t =\frac{T}{6}\Leftrightarrow T=1 (s)\Leftrightarrow \omega = \frac{2\pi}{T}=2\pi (rad/s)$ $\Delta t =\frac{T}{6}\Leftrightarrow T=1 (s)\Leftrightarrow \omega = \frac{2\pi}{T}=2\pi (rad/s)$

$Wđmax= \frac{1}{2}m\omega ^{2}A^{2}=0,02\Leftrightarrow A=\sqrt{\frac{2W_{dmax}}{m\omega ^{2}}}=\sqrt{\frac{2.0,02}{0,4.(2\pi) ^{2}}}=0,05 m = 5 (cm)$ $Wđmax= \frac{1}{2}m\omega ^{2}A^{2}=0,02\Leftrightarrow A=\sqrt{\frac{2W_{dmax}}{m\omega ^{2}}}=\sqrt{\frac{2.0,02}{0,4.(2\pi) ^{2}}}=0,05 m = 5 (cm)$

Tại $t=0: \left\{\begin{matrix} x_{0}=Acos\varphi=\frac{A}{2} & \\ v=-Asin \varphi >0 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} cos\varphi =\frac{1}{2} & \\ sin \varphi < 0 \end{matrix}\right. \Rightarrow \varphi =-\frac{\pi}{3}$ $t=0: \left\{\begin{matrix} x_{0}=Acos\varphi=\frac{A}{2} & \\ v=-Asin \varphi >0 \end{matrix}\right.\Rightarrow \left\{\begin{matrix} cos\varphi =\frac{1}{2} & \\ sin \varphi < 0 \end{matrix}\right. \Rightarrow \varphi =-\frac{\pi}{3}$

Phương trình dao động của vật: $x=5cos(2\pi t-\frac{\pi}{3}) (cm)$ $x=5cos(2\pi t-\frac{\pi}{3}) (cm)$

Bài 4 trang 30

Một vật có khối lượng m dao động điều hoà với tần số góc ở và biên độ A.

a) Khi vật có li độ bằng một nửa biên độ thì động năng và thế năng chiếm bao nhiêu phần trăm so với cơ năng?

b) Tại li độ nào thì thế năng bằng động năng?

Gợi ý đáp án

a) Ta có:

$x=\frac{A}{2} \Rightarrow \frac{W_{t}}{W}=\frac{\frac{1}{2}m\omega ^{2}x^{2}}{\frac{1}{2}m\omega ^{2}A^{2}}=\frac{1}{4}\Rightarrow Wt = 25%W; Wđ = 75%W$ $x=\frac{A}{2} \Rightarrow \frac{W_{t}}{W}=\frac{\frac{1}{2}m\omega ^{2}x^{2}}{\frac{1}{2}m\omega ^{2}A^{2}}=\frac{1}{4}\Rightarrow Wt = 25%W; Wđ = 75%W$

b) Ta có: $Wt=Wđ \Rightarrow \frac{W_{t}}{W}=\frac{\frac{1}{2}m\omega ^{2}x^{2}}{\frac{1}{2}m\omega ^{2}A^{2}}=\frac{1}{2}\Rightarrow x=\frac{A}{\sqrt{2}}$ $Wt=Wđ \Rightarrow \frac{W_{t}}{W}=\frac{\frac{1}{2}m\omega ^{2}x^{2}}{\frac{1}{2}m\omega ^{2}A^{2}}=\frac{1}{2}\Rightarrow x=\frac{A}{\sqrt{2}}$

Chia sẻ bởi: