Bài tập Nhân chia các số hữu tỉ Toán lớp 7 Nhân chia số hữu tỉ

Tải về Bình luận

Nhân chia số hữu tỉ thuộc dạng bài tập trọng tâm trong chương trình Toán 7. Chuyên đề Nhân chia số hữu tỉ bao gồm lý thuyết, các dạng toán và bài tập chuyên đề nhân, chia số hữu tỉ có đáp án kèm theo.

Toán lớp 7 Nhân chia số hữu tỉ được áp dụng với cả 3 bộ sách theo chương trình mới. Qua tài liệu này giúp các bạn học sinh nắm vững quy tắc nhân, chia hai số hữu tỉ, các tính chất của phép nhân số hữu tỉ. Từ đó vận dụng quy tắc nhân, chia số hữu tỉ để thực hiện phép tính, tính giá trị biểu thức. Vậy sau đây là Bài tập Nhân chia số hữu tỉ, mời các bạn cùng theo dõi tại đây.

Nhân chia số hữu tỉ

I. Lý thuyết Nhân chia các số hữu tỉ
II. Sơ đồ hóa Nhân chia số hữu tỉ
III. Ví dụ Nhân chia số hữu tỉ
IV. Bài tập Nhân chia các số hữu tỉ
V. Đáp án bài tập Nhân chia các số hữu tỉ

I. Lý thuyết Nhân chia các số hữu tỉ

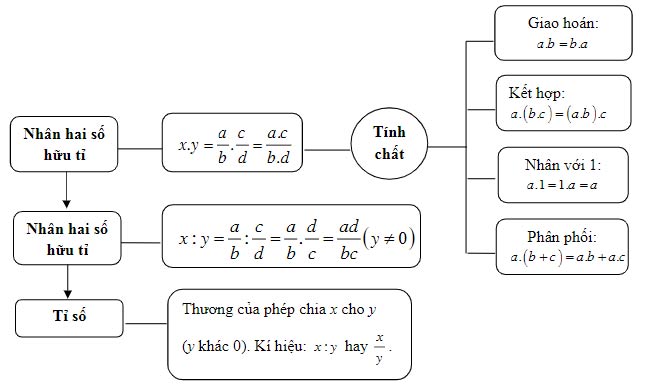
1. Nhân hai số hữu tỉ

+ Phép nhân số hữu tỉ có các tính chất của phép nhân phân số: giao hoán, kết hợp, nhân với số 1

+ Với $x = \frac{a}{b}$ $x = \frac{a}{b}$ và $y = \frac{c}{d}\left( {a,b,c,d \in Z} \right)$ $y = \frac{c}{d} (a, b, c, d \in Z)$ ta có: $x.y = \frac{a}{b}.\frac{c}{d} = \frac{{a.c}}{{b.d}}$ $x . y = \frac{a}{b} . \frac{c}{d} = \frac{a . c}{b . d}$

2. Chia hai số hữu tỉ

+ Với $x = \frac{a}{b}$ $x = \frac{a}{b}$ và $y = \frac{c}{d}$ $y = \frac{c}{d}$ ta có: $x:y = \frac{a}{b}:\frac{c}{d} = \frac{a}{b}.\frac{d}{c} = \frac{{a.d}}{{b.c}}$ $x : y = \frac{a}{b} : \frac{c}{d} = \frac{a}{b} . \frac{d}{c} = \frac{a . d}{b . c}$

+ Thương của phép chia số hữu tỉ x cho số hữu tỉ y (y khác 0) gọi là tỉ số của hai số x và y, kí hiệu là $\frac{x}{y}$ $\frac{x}{y}$ hay x : y

II. Sơ đồ hóa Nhân chia số hữu tỉ

III. Ví dụ Nhân chia số hữu tỉ

Ví dụ 1:

a) $\dfrac{-2}{7}.\dfrac{21}{8}$ $\frac{- 2}{7} . \frac{21}{8}$

b) $0,24.\dfrac{-15}{4}$ $0, 24. \frac{- 15}{4}$

c) $(-2).\left(-\dfrac{7}{12}\right)$ $(- 2) . (- \frac{7}{12})$

d) $\left(-\dfrac{3}{25}\right) : 6$ $(- \frac{3}{25}) : 6$

Trả lời

a) $\dfrac{-2}{7}.\dfrac{21}{8}$ $\frac{- 2}{7} . \frac{21}{8}$ $= \dfrac{-2.21}{7.8} = \dfrac{-3}{4};$ $= \frac{- 2.21}{7.8} = \frac{- 3}{4};$

b) $0,24.\dfrac{-15}{4}$ $0, 24. \frac{- 15}{4}$ $\dfrac{6}{25}.\dfrac{-15}{4} = \dfrac{6.(-15)}{25.4} = \dfrac{-9}{10};$ $\frac{6}{25} . \frac{- 15}{4} = \frac{6. (- 15)}{25.4} = \frac{- 9}{10};$

c) $(-2).\left(-\dfrac{7}{12}\right) = \dfrac{-2}{1}.\left(-\dfrac{7}{12}\right) = \dfrac{(-2).(-7)}{1.12} = \dfrac{7}{6};$ $(- 2) . (- \frac{7}{12}) = \frac{- 2}{1} . (- \frac{7}{12}) = \frac{(- 2) . (- 7)}{1.12} = \frac{7}{6};$

d) $\left(-\dfrac{3}{25}\right) : 6 = \left(-\dfrac{3}{25}\right). \dfrac{1}{6}= \dfrac{(-3).1}{25.6} = \dfrac{-1}{50}$ $(- \frac{3}{25}) : 6 = (- \frac{3}{25}) . \frac{1}{6} = \frac{(- 3) .1}{25.6} = \frac{- 1}{50}$

Ví dụ 2:

Ta có thể viết số hữu tỉ $\dfrac{-5}{16}$ $\frac{- 5}{16}$ dưới các dạng sau đây:

a) $\dfrac{-5}{16}$ $\frac{- 5}{16}$ là tích của hai số hữu tỉ. Ví dụ: $\dfrac{-5}{16} = \dfrac{-5}{2}.\dfrac{1}{8};$ $\frac{- 5}{16} = \frac{- 5}{2} . \frac{1}{8};$

b) $\dfrac{-5}{16}$ $\frac{- 5}{16}$ là thương của hai số hữu tỉ. Ví dụ: $\dfrac{-5}{16} = \dfrac{-5}{2} : 8$ $\frac{- 5}{16} = \frac{- 5}{2} : 8$

Với mỗi câu, em hãy tìm thêm một ví dụ.

Trả lời

Theo đề bài ta có:

a) $\dfrac{-5}{16} = \dfrac{-5}{4}.\dfrac{1}{4} = (-5).\dfrac{1}{16} = \dfrac{-5}{8}.\dfrac{1}{2};$ $\frac{- 5}{16} = \frac{- 5}{4} . \frac{1}{4} = (- 5) . \frac{1}{16} = \frac{- 5}{8} . \frac{1}{2};$

b) $\dfrac{-5}{16} = \dfrac{-5}{4} : 4 = \dfrac{-5}{8} : 2$ $\frac{- 5}{16} = \frac{- 5}{4} : 4 = \frac{- 5}{8} : 2$

Lưu ý: $\dfrac{a}{b}. \dfrac{c}{d} = \dfrac{a.c}{b.d}$ $\frac{a}{b} . \frac{c}{d} = \frac{a . c}{b . d}$

Ví dụ 3

Tính:

a) $\dfrac{-3}{4}.\dfrac{12}{-5}.\left(-\dfrac{25}{6}\right);$ $\frac{- 3}{4} . \frac{12}{- 5} . (- \frac{25}{6});$

b) $(-2).\dfrac{-38}{21}.\dfrac{-7}{4}.\left(-\dfrac{3}{8}\right);$ $(- 2) . \frac{- 38}{21} . \frac{- 7}{4} . (- \frac{3}{8});$

c) $\left(\dfrac{11}{12}:\dfrac{33}{16}\right).\dfrac{3}{5};$ $(\frac{11}{12} : \frac{33}{16}) . \frac{3}{5};$

d) $\dfrac{7}{23}.\left[\left(-\dfrac{8}{6}\right)-\dfrac{45}{18}\right]$ $\frac{7}{23} . [(- \frac{8}{6}) - \frac{45}{18}]$

Trả lời

a) $\dfrac{-3}{4}.\dfrac{12}{-5}.\left(-\dfrac{25}{6}\right)$ $\frac{- 3}{4} . \frac{12}{- 5} . (- \frac{25}{6})$

$= \dfrac{-3.(-12).(-25)}{4.5.6}$ $= \frac{- 3. (- 12) . (- 25)}{4.5 .6}$

$= \dfrac{-15}{2} = -7\dfrac{1}{2}$ $= \frac{- 15}{2} = - 7 \frac{1}{2}$

b) $(-2).\dfrac{-38}{21}.\dfrac{-7}{4}.\left(-\dfrac{3}{8}\right)$ $(- 2) . \frac{- 38}{21} . \frac{- 7}{4} . (- \frac{3}{8})$

$= \dfrac{(-2).(-38).(-7).(-3)}{21.4.8}$ $= \frac{(- 2) . (- 38) . (- 7) . (- 3)}{21.4 .8}$

$= \dfrac{19}{8} = 2\dfrac{3}{8}$ $= \frac{19}{8} = 2 \frac{3}{8}$

c) $\left(\dfrac{11}{12}:\dfrac{33}{16}\right).\dfrac{3}{5}$ $(\frac{11}{12} : \frac{33}{16}) . \frac{3}{5}$

$= \left(\dfrac{11}{12}.\dfrac{16}{33}\right).\dfrac{3}{5}$ $= (\frac{11}{12} . \frac{16}{33}) . \frac{3}{5}$

$= \dfrac{11.16.3}{12.33.5}$ $= \frac{11.16 .3}{12.33 .5}$

$= \dfrac{4}{15}$ $= \frac{4}{15}$

d) $\dfrac{7}{23}.\left[\left(-\dfrac{8}{6}\right)-\dfrac{45}{18}\right]$ $\frac{7}{23} . [(- \frac{8}{6}) - \frac{45}{18}]$

$= \dfrac{7}{23}.\dfrac{-24 - 25}{18}$ $= \frac{7}{23} . \frac{- 24 - 25}{18}$

$= \dfrac{7}{23}.\left(\dfrac{-69}{18}\right)$ $= \frac{7}{23} . (\frac{- 69}{18})$

$= \dfrac{7.(-69)}{23.18}$ $= \frac{7. (- 69)}{23.18}$

$= -\dfrac{7}{6}$ $= - \frac{7}{6}$

$= -1\dfrac{1}{6}$ $= - 1 \frac{1}{6}$

Ví dụ 4:

a) -0,32 . (-0,875)

$= \frac{{ - 32}}{{100}}.\left( {\frac{{ - 875}}{{1000}}} \right)$ $= \frac{- 32}{100} . (\frac{- 875}{1000})$

$= \frac{{ - 8}}{{25}}.\left( {\frac{{ - 7}}{8}} \right) = \frac{{ - 7}}{{25}}$ $= \frac{- 8}{25} . (\frac{- 7}{8}) = \frac{- 7}{25}$

b) $\left( { - 5} \right):2\frac{1}{5} = \left( { - 5} \right):\frac{{11}}{5} = \left( { - 5} \right).\frac{5}{{11}} = \frac{{ - 25}}{{11}}$ $(- 5) : 2 \frac{1}{5} = (- 5) : \frac{11}{5} = (- 5) . \frac{5}{11} = \frac{- 25}{11}$

Ví dụ 5:

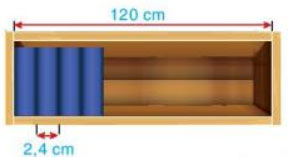
Ngăn đựng sách của một giá sách trong thư viện dài 120cm (xem hình bên). Người ta dự định xếp các cuốn sách dày khoảng 2,4 cm vào ngăn này. Hỏi ngăn sách đó có thể để được nhiều nhất bao nhiêu cuốn sách như vậy?

Bài 1.11

Gợi ý đáp án:

Ngăn sách đó có thể để được số sách nhiều nhất là:

120 : 2, 4 = 50 (cuốn sách)

Vậy có thể để được nhiều nhất 50 cuốn sách vào ngăn sách đó.

Ví dụ 6;

b) $\left( {7 - \frac{1}{2} - \frac{3}{4}} \right):\left( {5 - \frac{1}{4} - \frac{5}{8}} \right)$ $(7 - \frac{1}{2} - \frac{3}{4}) : (5 - \frac{1}{4} - \frac{5}{8})$

$= \left( {\frac{{28}}{4} - \frac{2}{4} - \frac{3}{4}} \right):\left( {\frac{{40}}{8} - \frac{2}{8} - \frac{5}{8}} \right)$ $= (\frac{28}{4} - \frac{2}{4} - \frac{3}{4}) : (\frac{40}{8} - \frac{2}{8} - \frac{5}{8})$

$= \left( {\frac{{28 - 2 - 3}}{4}} \right):\left( {\frac{{40 - 2 - 5}}{8}} \right)$ $= (\frac{28 - 2 - 3}{4}) : (\frac{40 - 2 - 5}{8})$

$= \frac{{23}}{4}:\frac{{33}}{8} = \frac{{23}}{4}.\frac{8}{{33}} = \frac{{46}}{{33}}$ $= \frac{23}{4} : \frac{33}{8} = \frac{23}{4} . \frac{8}{33} = \frac{46}{33}$

IV. Bài tập Nhân chia các số hữu tỉ

Câu 1: Kết quả của phép tính $\frac{{ - 3}}{4}.\frac{{16}}{{15}}$ $\frac{- 3}{4} . \frac{16}{15}$ bằng:

A. $\frac{{ - 5}}{4}$

\frac{- 5}{4}

B. $\frac{{ - 4}}{5}$

\frac{- 4}{5}

C. -1

D. $\frac{{ - 4}}{3}$

\frac{- 4}{3}

Câu 2: Kết quả của phép tính $\frac{{22}}{4}:\frac{{11}}{8}$ $\frac{22}{4} : \frac{11}{8}$ bằng:

A. 1

B. 2

C. 3

D. 4

Câu 3: Giá trị x thỏa mãn $\frac{3}{4}x = \frac{{15}}{{16}}$ $\frac{3}{4} x = \frac{15}{16}$ là:

A. $x = \frac{{ - 4}}{5}$

x = \frac{- 4}{5}

B. $x = \frac{4}{5}$

x = \frac{4}{5}

C. $x = \frac{{ - 5}}{4}$

x = \frac{- 5}{4}

D. $x = \frac{5}{4}$

x = \frac{5}{4}

Câu 4: $\frac{{ - 1}}{6}$ $\frac{- 1}{6}$ là kết quả của phép tính:

A. $\frac{{22}}{{14}}.\frac{7}{{11}}.\frac{1}{6}$ $\frac{22}{14} . \frac{7}{11} . \frac{1}{6}$	B. $\frac{3}{4}.\left( {\frac{{ - 7}}{{14}}} \right).\frac{4}{{21}}$ $\frac{3}{4} . (\frac{- 7}{14}) . \frac{4}{21}$
C. $\frac{5}{{16}}.\frac{8}{{15}}.2$ $\frac{5}{16} . \frac{8}{15} .2$	D. $\frac{{ - 4}}{{12}}.\left( {\frac{{ - 5}}{6}} \right).\left( {\frac{{ - 9}}{{15}}} \right)$ $\frac{- 4}{12} . (\frac{- 5}{6}) . (\frac{- 9}{15})$

Câu 5: Giá trị x thỏa mãn $x:\frac{5}{4} = \frac{8}{{15}}$ $x : \frac{5}{4} = \frac{8}{15}$ là:

A. $x = \frac{2}{3}$

x = \frac{2}{3}

B. $x = \frac{3}{2}$

x = \frac{3}{2}

C. $x = \frac{3}{4}$

x = \frac{3}{4}

D. $x = \frac{4}{3}$

x = \frac{4}{3}

Câu 6: Thực hiện phép tính:

a, $\frac{{ - 3}}{2}.\left( { - 0,08} \right)$ $\frac{- 3}{2} . (- 0, 08)$	b, $\left( {\frac{{ - 1}}{5}} \right).4\frac{1}{2}$ $(\frac{- 1}{5}) .4 \frac{1}{2}$	c, $- 3\frac{3}{4}:\left( { - 2,1} \right)$ $- 3 \frac{3}{4} : (- 2, 1)$
d, $\left( { - 8\frac{2}{5}} \right).\frac{5}{{ - 14}}$ $(- 8 \frac{2}{5}) . \frac{5}{- 14}$	e, $- 3,5:\frac{{21}}{4}$ $- 3, 5 : \frac{21}{4}$	f, $1\frac{2}{3}.\left( {\frac{{ - 7}}{3}} \right)$ $1 \frac{2}{3} . (\frac{- 7}{3})$

Câu 7: Tìm số hữu tỉ x, biết:

a, $\frac{2}{3} - 1\frac{4}{{15}}x = \frac{{ - 3}}{5}$ $\frac{2}{3} - 1 \frac{4}{15} x = \frac{- 3}{5}$	b, $1\frac{1}{2}.x - 4 = 0,5$ $1 \frac{1}{2} . x - 4 = 0, 5$
c, $\frac{x}{{12}} - \frac{5}{6} = \frac{1}{{12}}$ $\frac{x}{12} - \frac{5}{6} = \frac{1}{12}$	d, $2\frac{2}{3}:x = 1\frac{7}{9}:2\frac{2}{3}$ $2 \frac{2}{3} : x = 1 \frac{7}{9} : 2 \frac{2}{3}$

Câu 8: Viết số hữu tỉ $\frac{{ - 25}}{{16}}$ $\frac{- 25}{16}$ dưới các dạng:

a, Tích của hai số hữu tỉ có một thừa số là $\frac{{ - 5}}{{12}}$ $\frac{- 5}{12}$

b, Thương của hai số hữu tỉ, trong đó số bị chia là $\frac{{ - 4}}{5}$ $\frac{- 4}{5}$

V. Đáp án bài tập Nhân chia các số hữu tỉ

Câu 1	Câu 2	Câu 3	Câu 4	Câu 5
B	D	D	C	A

Câu 6

a, $\frac{{ - 3}}{2}.\left( { - 0,08} \right) = \frac{3}{{25}}$ $\frac{- 3}{2} . (- 0, 08) = \frac{3}{25}$	b, $\left( {\frac{{ - 1}}{5}} \right).4\frac{1}{2} = \frac{{ - 9}}{{10}}$ $(\frac{- 1}{5}) .4 \frac{1}{2} = \frac{- 9}{10}$	c, $- 3\frac{3}{4}:\left( { - 2,1} \right) = \frac{{25}}{{14}}$ $- 3 \frac{3}{4} : (- 2, 1) = \frac{25}{14}$
d, $\left( { - 8\frac{2}{5}} \right).\frac{5}{{ - 14}} = 3$ $(- 8 \frac{2}{5}) . \frac{5}{- 14} = 3$	e, $- 3,5:\frac{{21}}{4} = \frac{{ - 2}}{3}$ $- 3, 5 : \frac{21}{4} = \frac{- 2}{3}$	f, $1\frac{2}{3}.\left( {\frac{{ - 7}}{3}} \right) = \frac{{ - 35}}{9}$ $1 \frac{2}{3} . (\frac{- 7}{3}) = \frac{- 35}{9}$

Câu 7:

x = 1

x = 3

x = 11

d, $% MathType!MTEF!2!1!+- % feaahqart1ev3aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn % hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr % 4rNCHbGeaGqipv0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9 % vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x % fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamiEaiabg2 % da9maalaaabaGaaGymaaqaaiaaisdaaaaaaa!39A0! $x = \frac{1}{4}$

Câu 8

a, $\frac{{ - 25}}{{16}} = \frac{{ - 5}}{{12}}.\frac{{15}}{4}$ $\frac{- 25}{16} = \frac{- 5}{12} . \frac{15}{4}$

b, $\frac{{ - 25}}{{16}} = \frac{{ - 4}}{5}:\frac{{64}}{{125}}$ $\frac{- 25}{16} = \frac{- 4}{5} : \frac{64}{125}$

Chia sẻ bởi:

Thu Thảo

Tải về

Liên kết tải về

Bài tập Nhân chia các số hữu tỉ 411,9 KB Tải về

Tìm thêm: Toán lớp 7 Toán 7

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!