Tổng và hiệu của hai vectơ Ôn tập Toán 10

Tải về Bình luận

Tổng và hiệu của hai vectơ là tài liệu vô cùng hữu ích không thể thiếu dành cho các học sinh lớp 10 tham khảo. Tổng và hiệu của hai vectơ sẽ được học trong chương trình Toán 10 học kì 1 áp dụng đối với cả 3 bộ sách giáo khoa.

Bài tập tổng và hiệu của hai vectơ lớp 10 bao gồm 7 trang tóm tắt toàn bộ kiến thức lý thuyết và các dạng bài tập, phương pháp giải có đáp án kèm theo. Tài liệu được biên soạn rất khoa học, phù hợp với mọi đối tượng học sinh. Qua đó giúp học sinh củng cố, nắm vững chắc kiến thức nền tảng, vận dụng với các bài tập cơ bản để đạt được điểm số cao trong kì thi học kì 1 lớp 10. Bên cạnh đó các bạn xem thêm tài liệu Bài tập tự luận chuyên đề vectơ.

Tổng và hiệu của hai vectơ

I. Tổng của hai vectơ
II. Hiệu của hai vectơ
III. Áp dụng tổng và hiệu hai vecto
IV. Các dạng bài tập tổng và hiệu của vectơ
V. Bài tập tổng và hiệu của hai vectơ

I. Tổng của hai vectơ

1. Tổng của hai vectơ

Định nghĩa: Cho hai vectơ $\overrightarrow{a}, \overrightarrow{b}$ $\overrightarrow{a}, \overrightarrow{b}$. Lấy một điểm A tùy ý, vẽ $\overrightarrow{AB} = \overrightarrow{a}, \overrightarrow{BC} = \overrightarrow{b}$ $\overrightarrow{AB} = \overrightarrow{a}, \overrightarrow{BC} = \overrightarrow{b}$. Vectơ $\overrightarrow{AC}$ $\overrightarrow{AC}$ được gọi là tổng của hai vectơ $\overrightarrow{a}$ $\overrightarrow{a}$ và $\overrightarrow{b}.$ $\overrightarrow{b}.$

$\overrightarrow{AC} = \overrightarrow{a} + \overrightarrow{b}.$ $\overrightarrow{AC} = \overrightarrow{a} + \overrightarrow{b}.$

2. Quy tắc hình bình hành

Nếu ABCD là hình bình hành thì

$\overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{AC}.$ $\overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{AC}.$

3. Tính chất của tổng các vectơ

- Tính chất giao hoán

$\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}$ $\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}$

- Tính chất kết hợp

$(\overrightarrow{a} + \overrightarrow{b} ) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} +\overrightarrow{c})$ $(\overrightarrow{a} + \overrightarrow{b} ) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} +\overrightarrow{c})$

- Tính chất của $\overrightarrow{0}$ $\overrightarrow{0}$:

$\overrightarrow{a}+\overrightarrow{0} = \overrightarrow{0} + \overrightarrow{a} =\overrightarrow{a}$ $\overrightarrow{a}+\overrightarrow{0} = \overrightarrow{0} + \overrightarrow{a} =\overrightarrow{a}$

II. Hiệu của hai vectơ

a) Vec tơ đối: Vectơ có cùng độ dài và ngược hướng với vec tơ $\overrightarrow{a}$ $\overrightarrow{a}$ được gọi là vec tơ đối của vec tơ $\overrightarrow{a}$ $\overrightarrow{a}$ , kí hiệu $-\overrightarrow{a}.$ $-\overrightarrow{a}.$

Vec tơ đối của $\overrightarrow{0}$ $\overrightarrow{0}$ là vectơ $\overrightarrow{0}.$ $\overrightarrow{0}.$

b) Hiệu của hai vec tơ: Cho hai vectơ $\overrightarrow{a}, \overrightarrow{b}$ $\overrightarrow{a}, \overrightarrow{b}$. Vec tơ hiệu của hai vectơ, kí hiệu $\overrightarrow{a}- \overrightarrow{b}$ $\overrightarrow{a}- \overrightarrow{b}$ là vectơ $\overrightarrow{a} + (-\overrightarrow{b})$ $\overrightarrow{a} + (-\overrightarrow{b})$

$\overrightarrow{a}- \overrightarrow{b} = \overrightarrow{a} + (-\overrightarrow{b}).$ $\overrightarrow{a}- \overrightarrow{b} = \overrightarrow{a} + (-\overrightarrow{b}).$

c) Chú ý: Với ba điểm bất kì, ta luôn có

$\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC} (1)$ $\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC} (1)$

$\overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{CB} (2)$ $\overrightarrow{AB} - \overrightarrow{AC} = \overrightarrow{CB} (2)$

(1) là quy tắc 3 điểm (quy tắc tam giác) đối với tổng của hai vectơ.

(2) là quy tắc 3 điểm (quy tắc tam giác) đối với hiệu các vectơ.

III. Áp dụng tổng và hiệu hai vecto

a) Trung điểm của đoạn thẳng:

I là trung điểm của đoạn thẳng

$⇔ \overrightarrow{IA} +\overrightarrow{IB} = \overrightarrow{0}$ $⇔ \overrightarrow{IA} +\overrightarrow{IB} = \overrightarrow{0}$

b) Trọng tâm của tam giác:

G là trọng tâm của tam giác ∆ABC

$⇔ \overrightarrow{GA} + \overrightarrow{GB}+\overrightarrow{GC} = \overrightarrow{0}$ $⇔ \overrightarrow{GA} + \overrightarrow{GB}+\overrightarrow{GC} = \overrightarrow{0}$

IV. Các dạng bài tập tổng và hiệu của vectơ

Dạng 1: Xác định độ dài tổng và hiệu của các vectơ

Phương pháp giải:

Sử dụng định nghĩa về tổng và hiệu của các vectơ và các tính chất, quy tắc để xác định phép toán vectơ đó
Dựa vào tính chất của hình học, sử dụng định lý Pitago, hệ thức lượng trong tam giác vuông để xác định độ dài vectơ đó.

Ví dụ 1: Cho tam giác ABC vuông tại A có $\widehat{ABC}=30^\circ$ $\widehat{ABC}=30^\circ$ và $BC=a\sqrt5$ $BC=a\sqrt5$. Tính độ dài của các vectơ $\overrightarrow{AB}+\overrightarrow{BC},\overrightarrow{AC}-\overrightarrow{BC}$ $\overrightarrow{AB}+\overrightarrow{BC},\overrightarrow{AC}-\overrightarrow{BC}$ và $\overrightarrow{AB}+\overrightarrow{AC}$ $\overrightarrow{AB}+\overrightarrow{AC}$

Cách giải:

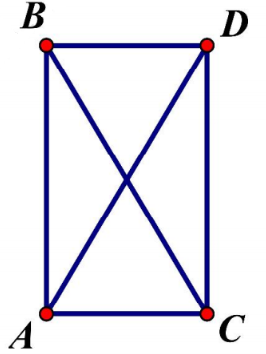
Theo quy tắc ba điểm:

$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$

Mà $\sin{ABC}=\frac{AC}{BC}$ $\sin{ABC}=\frac{AC}{BC}$

$\Rightarrow AC=BC.\sin{ABC}=a\sqrt5.\sin{30^\circ}=\frac{a\sqrt5}{2}$ $\Rightarrow AC=BC.\sin{ABC}=a\sqrt5.\sin{30^\circ}=\frac{a\sqrt5}{2}$

Do đó $\left | \overrightarrow{AB}+\overrightarrow{BC} \right |=\left | \overrightarrow{AC} \right |=AC=\frac{a\sqrt5}{2}$ $\left | \overrightarrow{AB}+\overrightarrow{BC} \right |=\left | \overrightarrow{AC} \right |=AC=\frac{a\sqrt5}{2}$

$\overrightarrow{AC}-\overrightarrow{BC}= \overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AB}$ $\overrightarrow{AC}-\overrightarrow{BC}= \overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AB}$

Ta có: $AC^2+AB^2-BC^2\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{5a^2-\frac{5a^2}{4}}=\frac{a\sqrt{15}}{2}$ $AC^2+AB^2-BC^2\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{5a^2-\frac{5a^2}{4}}=\frac{a\sqrt{15}}{2}$

Vì vậy $\left | \overrightarrow{AC}-\overrightarrow{BC} \right |=\left | \overrightarrow{AB} \right |=AB=\frac{a\sqrt{15}}{2}$ $\left | \overrightarrow{AC}-\overrightarrow{BC} \right |=\left | \overrightarrow{AB} \right |=AB=\frac{a\sqrt{15}}{2}$

Gọi D là điểm sao cho tứ giác ABCD là hình bình hành

Khi đó theo quy tắc hình bình hành ta có $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}$ $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}$

Vì tam giác ABC vuông ở A nên tứ giác ABCD là hình chữ nhật suy ra $AD=BC=a\sqrt5$ $AD=BC=a\sqrt5$

Vậy $\left | \overrightarrow{AB}+\overrightarrow{AC} \right |=\left | \overrightarrow{AD} \right |=AD= a\sqrt5$ $\left | \overrightarrow{AB}+\overrightarrow{AC} \right |=\left | \overrightarrow{AD} \right |=AD= a\sqrt5$

Dạng 2: Chứng minh các đẳng thức vectơ từ việc biến đổi

Phương pháp giải: Để chứng minh đẳng thức vectơ ta có các cách biến đổi: Vế này thành vế kia, biến đổi tương đương, biến đổi hai vế cùng bằng một đại lượng trung gian. Trong quá trình biến đổi ta cần sử dụng linh hoạt các quy tắc vectơ.

Ví dụ 1: Cho năm điểm A,B,C,D,E. Chứng minh rằng:

$\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{EA}=\overrightarrow{CB}+\overrightarrow{ED}$ $\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{EA}=\overrightarrow{CB}+\overrightarrow{ED}$

$\overrightarrow{AC}+\overrightarrow{CD}-\overrightarrow{EC}=\overrightarrow{AE}-\overrightarrow{DB}+\overrightarrow{CB}$ $\overrightarrow{AC}+\overrightarrow{CD}-\overrightarrow{EC}=\overrightarrow{AE}-\overrightarrow{DB}+\overrightarrow{CB}$

Cách giải:

1. Biến đổi vế trái ta có:

$\begin{align}\nonumber VT&=\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{CD}+\overrightarrow{ED}+\overrightarrow{DA}\\ \nonumber&=\overrightarrow{CB}+\overrightarrow{ED}+\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DA}\\ \nonumber&=\overrightarrow{CB}+\overrightarrow{ED}+\overrightarrow{AD}+\overrightarrow{DA}\\ \nonumber&=\overrightarrow{CB}+\overrightarrow{ED}=VP \end{align} (ĐPCM)$ $\begin{align}\nonumber VT&=\overrightarrow{AC}+\overrightarrow{CB}+\overrightarrow{CD}+\overrightarrow{ED}+\overrightarrow{DA}\\ \nonumber&=\overrightarrow{CB}+\overrightarrow{ED}+\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DA}\\ \nonumber&=\overrightarrow{CB}+\overrightarrow{ED}+\overrightarrow{AD}+\overrightarrow{DA}\\ \nonumber&=\overrightarrow{CB}+\overrightarrow{ED}=VP \end{align} (ĐPCM)$

2. Đẳng thức tương đương với

$\overrightarrow{AC}-\overrightarrow{AE}+\overrightarrow{CD}-\overrightarrow{CB}- \overrightarrow{EC}+\overrightarrow{DB}=\overrightarrow{0}$ $\overrightarrow{AC}-\overrightarrow{AE}+\overrightarrow{CD}-\overrightarrow{CB}- \overrightarrow{EC}+\overrightarrow{DB}=\overrightarrow{0}$

$\Leftrightarrow\overrightarrow{EC}+\overrightarrow{BD}-\overrightarrow{EC}+\overrightarrow{DB}=\overrightarrow{0}$ $\Leftrightarrow\overrightarrow{EC}+\overrightarrow{BD}-\overrightarrow{EC}+\overrightarrow{DB}=\overrightarrow{0}$

$\ \overrightarrow{BD}+\overrightarrow{DB}=\overrightarrow{0}$ $\ \overrightarrow{BD}+\overrightarrow{DB}=\overrightarrow{0}$ (ĐPCM)

Ví dụ 2: Cho hình bình hành ABCD tâm O. M là một điểm bất kì trong mặt phẳng. Chứng minh rằng:

$\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}=\overrightarrow{0}$ $\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}=\overrightarrow{0}$

$\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}$ $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}$

$\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{OD}$ $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{OD}$

Cách giải:

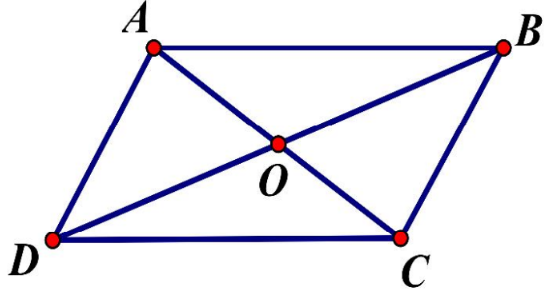
Ta có:

$\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}=-\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{AC}\\$ $\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}=-\overrightarrow{AB}-\overrightarrow{AD}+\overrightarrow{AC}\\$

$=-\left (\overrightarrow{AB}+\overrightarrow{AD} \right )+\overrightarrow{AC}$ $=-\left (\overrightarrow{AB}+\overrightarrow{AD} \right )+\overrightarrow{AC}$

Theo quy tắc hình bình hành ta có $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ suy ra:

$\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}=-\overrightarrow{AC}+\overrightarrow{AC}=\overrightarrow{0}$ $\overrightarrow{BA}+\overrightarrow{DA}+\overrightarrow{AC}=-\overrightarrow{AC}+\overrightarrow{AC}=\overrightarrow{0}$

2. Vì ABCD là hình bình hành nên ta có: $\overrightarrow{OA}=\overrightarrow{CO}\Rightarrow\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{CO}+\overrightarrow{OC}=\overrightarrow{0}$ $\overrightarrow{OA}=\overrightarrow{CO}\Rightarrow\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{CO}+\overrightarrow{OC}=\overrightarrow{0}$

Tương tự: $\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}\Rightarrow\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}$ $\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}\Rightarrow\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}$

3. Vì ABCD là hình bình hành nên:

$\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{BA}+\overrightarrow{AB}=\overrightarrow{0}$ $\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{BA}+\overrightarrow{AB}=\overrightarrow{0}$

$\begin{align}\nonumber\Rightarrow\overrightarrow{MA}+\overrightarrow{MC}&=\overrightarrow{MB}+\overrightarrow{BA}+\overrightarrow{MD}+\overrightarrow{DC}\\ \nonumber&=\overrightarrow{MB}+\overrightarrow{MD}+\overrightarrow{BA}+\overrightarrow{DC}\\ \nonumber&=\overrightarrow{MB}+\overrightarrow{MD} \end{align} (ĐPCM).$ $\begin{align}\nonumber\Rightarrow\overrightarrow{MA}+\overrightarrow{MC}&=\overrightarrow{MB}+\overrightarrow{BA}+\overrightarrow{MD}+\overrightarrow{DC}\\ \nonumber&=\overrightarrow{MB}+\overrightarrow{MD}+\overrightarrow{BA}+\overrightarrow{DC}\\ \nonumber&=\overrightarrow{MB}+\overrightarrow{MD} \end{align} (ĐPCM).$

V. Bài tập tổng và hiệu của hai vectơ

Bài 1

Cho hình bình hành ABCD có O là giao điểm hai đường chéo và một điểm M tùy ý. Chứng minh rằng:

$a) \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {0;}$ $a) \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {0;}$

$b) \overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD}$ $b) \overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD}$

Gợi ý đáp án

a) ABCD là hình bình hành nên $\overrightarrow {DC} = \overrightarrow {AB}$ $\overrightarrow {DC} = \overrightarrow {AB}$

$\Rightarrow \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {BA} + \overrightarrow {AB} = \overrightarrow {BB} = \overrightarrow 0$ $\Rightarrow \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {BA} + \overrightarrow {AB} = \overrightarrow {BB} = \overrightarrow 0$

$b) \overrightarrow {MA} + \overrightarrow {MC} = \left( {\overrightarrow {MB} + \overrightarrow {BA} } \right) + \left( {\overrightarrow {MD} + \overrightarrow {DC} } \right)$ $b) \overrightarrow {MA} + \overrightarrow {MC} = \left( {\overrightarrow {MB} + \overrightarrow {BA} } \right) + \left( {\overrightarrow {MD} + \overrightarrow {DC} } \right)$

$= \overrightarrow {MB} + \overrightarrow {MD} (Vì \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {0} )$ $= \overrightarrow {MB} + \overrightarrow {MD} (Vì \overrightarrow {BA} + \overrightarrow {DC} = \overrightarrow {0} )$

Bài 2

Cho tứ giác ABCD, thực hiện cả phép cộng và trừ vectơ sau:

$a) \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA};$ $a) \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA};$

$b) \overrightarrow {AB} - \overrightarrow {AD}$ $b) \overrightarrow {AB} - \overrightarrow {AD}$

$c) \overrightarrow {CB} - \overrightarrow {CD}$ $c) \overrightarrow {CB} - \overrightarrow {CD}$.

Gợi ý đáp án

a) $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DA} } \right)$ $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DA} } \right)$

$= \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow {AA} = \overrightarrow 0$ $= \overrightarrow {AC} + \overrightarrow {CA} = \overrightarrow {AA} = \overrightarrow 0$

$b) \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DA} + \overrightarrow {AB} = \overrightarrow {DB}$ $b) \overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {DA} = \overrightarrow {DA} + \overrightarrow {AB} = \overrightarrow {DB}$

$c) \overrightarrow {CB} - \overrightarrow {CD} = \overrightarrow {CB} + \overrightarrow {DC} = \overrightarrow {DC} + \overrightarrow {CB} = \overrightarrow {DB}$ $c) \overrightarrow {CB} - \overrightarrow {CD} = \overrightarrow {CB} + \overrightarrow {DC} = \overrightarrow {DC} + \overrightarrow {CB} = \overrightarrow {DB}$

Bài 3

Cho tam giác đều ABC cạnh bằng a. Tính độ dài các vectơ:

$a) \overrightarrow {BA} + \overrightarrow {AC} ;$ $a) \overrightarrow {BA} + \overrightarrow {AC} ;$

$b) \overrightarrow {AB} + \overrightarrow {AC} ;$ $b) \overrightarrow {AB} + \overrightarrow {AC} ;$

$c) \overrightarrow {BA} - \overrightarrow {BC} .$ $c) \overrightarrow {BA} - \overrightarrow {BC} .$

Gợi ý đáp án

$a) \overrightarrow {BA} + \overrightarrow {AC} = \overrightarrow {BC} \Rightarrow \left| {\overrightarrow {BC} } \right| = BC = a$ $a) \overrightarrow {BA} + \overrightarrow {AC} = \overrightarrow {BC} \Rightarrow \left| {\overrightarrow {BC} } \right| = BC = a$

b) Dựng hình bình hành ABDC, giao điểm của hai đường chéo là O ta có:

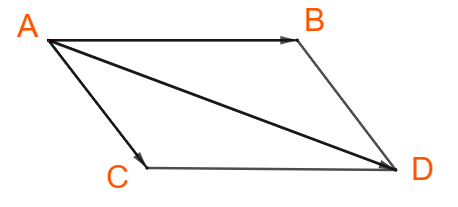
$\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD}$ $\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD}$

$AD = 2AO = 2\sqrt {A{B^2} - B{O^2}} = 2\sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = a\sqrt 3$ $AD = 2AO = 2\sqrt {A{B^2} - B{O^2}} = 2\sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = a\sqrt 3$

$\Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = a\sqrt 3$ $\Rightarrow \left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = a\sqrt 3$

$c) \overrightarrow {BA} - \overrightarrow {BC} = \overrightarrow {BA} + \overrightarrow {CB} = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA}$ $c) \overrightarrow {BA} - \overrightarrow {BC} = \overrightarrow {BA} + \overrightarrow {CB} = \overrightarrow {CB} + \overrightarrow {BA} = \overrightarrow {CA}$

$\Rightarrow \left| {\overrightarrow {BA} - \overrightarrow {BC} } \right| = \left| {\overrightarrow {CA} } \right| = CA = a$ $\Rightarrow \left| {\overrightarrow {BA} - \overrightarrow {BC} } \right| = \left| {\overrightarrow {CA} } \right| = CA = a$

Bài 5

Cho ba lực $\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} và \overrightarrow {{F_3}} = \overrightarrow {MC}$ $\overrightarrow {{F_1}} = \overrightarrow {MA} ,\overrightarrow {{F_2}} = \overrightarrow {MB} và \overrightarrow {{F_3}} = \overrightarrow {MC}$ cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}}$ $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}}$ đều là 10 N và $\widehat {AMB} = 90^\circ$ $\widehat {AMB} = 90^\circ$ Tìm độ lớn của lực $\overrightarrow {{F_3}} .$ $\overrightarrow {{F_3}} .$

Gợi ý đáp án

Ba lực $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}}$ $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}}$ cùng tác dụng vào M và vật đứng yên nên hợp lực của chúng có giá trị bằng không, hay: $\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0$ $\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0$

Dựng hình bình hành MADB, khi đó: $\overrightarrow {MA} + \overrightarrow {MB}= \overrightarrow {MD}$ $\overrightarrow {MA} + \overrightarrow {MB}= \overrightarrow {MD}$

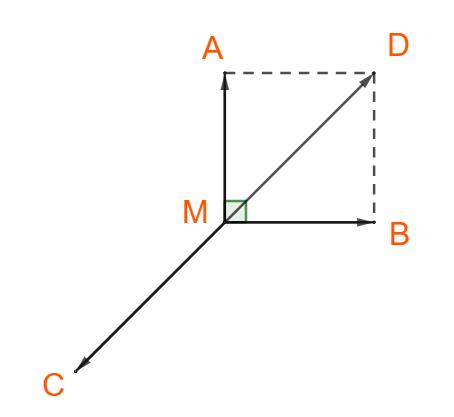
$\Rightarrow \overrightarrow {MD} + \overrightarrow {MC} = \overrightarrow {0}$ $\Rightarrow \overrightarrow {MD} + \overrightarrow {MC} = \overrightarrow {0}$

$\Rightarrow \overrightarrow {MD}, \overrightarrow {MC}$ $\Rightarrow \overrightarrow {MD}, \overrightarrow {MC}$ là hai vecto đối nhau

$\Rightarrow MD =MC$ $\Rightarrow MD =MC$

Xét hình bình hành MADB, ta có:

AM=AB và $\widehat {AMB} = 90^\circ$ $\widehat {AMB} = 90^\circ$

$\Rightarrow$ $\Rightarrow$ MADB là hình vuông, cạnh AB=10

$\Rightarrow MC = MD = AB. \sqrt{2} = 10\sqrt{2}$ $\Rightarrow MC = MD = AB. \sqrt{2} = 10\sqrt{2}$

Vậy độ lớn của lực $\overrightarrow {{F_3}}$ $\overrightarrow {{F_3}}$ là $\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MC} } \right| = MC = 10\sqrt 2 (N)$ $\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MC} } \right| = MC = 10\sqrt 2 (N)$

Chia sẻ bởi: