Toán 10 Bài tập cuối chương VII - Kết nối tri thức với cuộc sống Giải SGK Toán 10 trang 58, 59 - Tập 2

Mục lục

Giải Toán 10 Bài tập cuối chương VII: Phương pháp tọa độ trong mặt phẳng sách Kết nối tri thức với cuộc sống là tài liệu vô cùng hữu ích giúp các em học sinh lớp 10 có thêm nhiều gợi ý tham khảo, dễ dàng đối chiếu kết quả khi làm bài tập toán trang 58, 59 tập 2.

Giải SGK Toán 10 Bài tập cuối chương 7 tập 2 được biên soạn chi tiết, bám sát nội dung trong sách giáo khoa. Mỗi bài toán đều được giải thích cụ thể, chi tiết. Qua đó giúp các em củng cố, khắc sâu thêm kiến thức đã học trong chương trình chính khóa; có thể tự học, tự kiểm tra được kết quả học tập của bản thân.

Giải Toán 10 trang 34 Kết nối tri thức với cuộc sống - Tập 2

Bài 7.26 trang 58

Phương trình nào sau đây là phương trình tham số của đường thẳng?

A. 2x - y +1 = 0.

$B. \left\{\begin{matrix}x=2t\\ y=t\end{matrix}\right.$ $B . {\begin{matrix} x = 2 t \\ y = t \end{matrix}$

C. x² + y² =1.

D. y = 2x + 3

Gợi ý đáp án

Đáp án B

Bài 7.27 trang 58

Phương trình nào sau đây là phương trình tổng quát của đường thẳng?

A. -x - 2y + 3 = 0

$B. \left\{\begin{matrix}x=2+t\\ y=3-t\end{matrix}\right.$ $B . {\begin{matrix} x = 2 + t \\ y = 3 - t \end{matrix}$

C. y² = 2x

D. $\frac{x^{2}}{10}+\frac{y^{2}}{6}=1$ $\frac{x^{2}}{10} + \frac{y^{2}}{6} = 1$

Gợi ý đáp án

Đáp án A

Bài 7.28 trang 58

Phương trình nào sau đây là phương trình của đường tròn?

A. x² - y² =1

B. (x -1)2 + (y-2)² = -4

C. x² + y² =2

D. y² = 8x.

Gợi ý đáp án

Đáp án C

Bài 7.29 trang 58

Phương trình nào sau đây là phương trình chính tắc của đường elip?

$A. \frac{x^{2}}{9}+\frac{y^{2}}{9}=1$ $A . \frac{x^{2}}{9} + \frac{y^{2}}{9} = 1$

$B. \frac{x^{2}}{1}+\frac{y^{2}}{6}=1$ $B . \frac{x^{2}}{1} + \frac{y^{2}}{6} = 1$

$C. \frac{x^{2}}{4}-\frac{y^{2}}{1}=1$ $C . \frac{x^{2}}{4} - \frac{y^{2}}{1} = 1$

$D. \frac{x^{2}}{2}+\frac{y^{2}}{1}=1$ $D . \frac{x^{2}}{2} + \frac{y^{2}}{1} = 1$

Gợi ý đáp án

Đáp án D

Bài 7.30 trang 58

Phương trình nào sau đây là phương trình chính tắc của đường hypebol?

$A. \frac{x^{2}}{3}-\frac{y^{2}}{2}=1$ $A . \frac{x^{2}}{3} - \frac{y^{2}}{2} = 1$

$B. \frac{x^{2}}{1}-\frac{y^{2}}{6}=1$ $B . \frac{x^{2}}{1} - \frac{y^{2}}{6} = 1$

$C. \frac{x^{2}}{6}+\frac{y^{2}}{1}=1$ $C . \frac{x^{2}}{6} + \frac{y^{2}}{1} = 1$

$D. \frac{x^{2}}{2}-\frac{y^{2}}{1}=1$ $D . \frac{x^{2}}{2} - \frac{y^{2}}{1} = 1$

Gợi ý đáp án

Đáp án B

Bài 7.31 trang 58

Phương trình nào sau đây là phương trình chính tắc của đường parabol?

A. x ² = 4y

B. x ² = -6y

C. y ² = 4x

D. y ² = -4x

Gợi ý đáp án

Đáp án C

Bài 7.32 trang 58

Trong mặt phẳng tọa độ, cho A(1; -1), B(3; 5), C(-2; 4). Tính diện tích tam giác ABC.

Gợi ý đáp án

Viết phương trình đường thẳng BC: có vectơ chỉ phương là $\overrightarrow{BC}(-5;-1)$ $\vec{B C} (- 5; - 1)$ và đi qua B(3; 5).

$\Rightarrow$ $\Rightarrow$ Đường thẳng BC có vectơ pháp tuyến là: $\overrightarrow{n}(1; -5)$ $\vec{n} (1; - 5)$

$\Rightarrow$ $\Rightarrow$ Phương trình đường thẳng BC là: 1(x - 3) - 5(y - 5) = 0, Hay x - 5y +22 = 0

Độ dài đường cao kẻ từ A của tam giác ABC chính là khoảng cách từ A đến đường thẳng BC.

Áp dụng công thức khoảng cách có: $d_{(A; BC)}=\frac{|1.1-5.(-1)+22|}{\sqrt{1^{2}+5^{2}}}=\frac{14\sqrt{26}}{13}$ $d_{(A; B C)} = \frac{| 1.1 - 5. (- 1) + 22 |}{\sqrt{1^{2} + 5^{2}}} = \frac{14 \sqrt{26}}{13}$

Độ dài đoạn BC là: $BC = \sqrt{1^{2}+5^{2}}=\sqrt{26}$ $B C = \sqrt{1^{2} + 5^{2}} = \sqrt{26}$

Diện tích tam giác ABC là:

$S_{ABC}=\frac{1}{2}d_{(A;BC)}.BC=\frac{1}{2}.\frac{14\sqrt{26}}{13}.\sqrt{26}=14$ $S_{A B C} = \frac{1}{2} d_{(A; B C)} . B C = \frac{1}{2} . \frac{14 \sqrt{26}}{13} . \sqrt{26} = 14$

Bài 7.33 trang 58

Trong mặt phẳng tọa độ, cho hai điểm A(-1; 0) và B(3; 1).

a. Viết phương trình đường tròn tâm A và đi qua B.

b. Viết phương trình tổng quát của đường thẳng AB.

c. Viết phương trình đường tròn tâm O và tiếp xúc với đường thẳng AB.

Gợi ý đáp án

a. Đường tròn có bán kính là $AB = \sqrt{(3+1)^{2}+(1-0)^{2}}=\sqrt{17} = R$ $A B = \sqrt{(3 + 1)^{2} + (1 - 0)^{2}} = \sqrt{17} = R$

$\Rightarrow$ $\Rightarrow$ Phương trình đường tròn tâm A bán kính AB là: (x +1)² + y² = 17

b. Đường thẳng AB có vectơ chỉ phương $\overrightarrow{AB}(4;1).$ $\vec{A B} (4; 1) .$

$\Rightarrow$ $\Rightarrow$ Đường thẳng AB có vectơ pháp tuyến là: $\overrightarrow{n}(1; -4)$ $\vec{n} (1; - 4)$

$\Rightarrow$ $\Rightarrow$ Phương trình đường thẳng AB là: 1.(x +1) - 4(y - 0) = 0, Hay x - 4y +1 = 0

c. Khoảng cách từ O đến đường thẳng AB là:

$d_{(O; AB)}=\frac{|0-4.0+1|}{\sqrt{1^{2}+4^{2}}}=\frac{\sqrt{17}}{17}$ $d_{(O; A B)} = \frac{| 0 - 4.0 + 1 |}{\sqrt{1^{2} + 4^{2}}} = \frac{\sqrt{17}}{17}$

Khoảng cách từ O đến AB là bán kính của đường tròn cần tìm.

$\Rightarrow$ $\Rightarrow$ Phương trình đường tròn tâm O, bán kính $R = \frac{\sqrt{17}}{17} là: x2 + y2 = \frac{1}{17}$ $R = \frac{\sqrt{17}}{17} l à : x 2 + y 2 = \frac{1}{17}$

Bài 7.34 trang 58

Cho đường tròn (C) có phương trình x² + y² - 4x + 6y -12 = 0.

a. Tìm tọa độ tâm I và bán kính R của (C).

b. Chứng minh rằng điểm M(5; 1) thuộc (C). Viết phương trình tiếp tuyến d của (C) tại M.

Gợi ý đáp án

a. Tâm I(2; -3) và bán kính $R = \sqrt{2^{2}+3^{2}+12}=5$ $R = \sqrt{2^{2} + 3^{2} + 12} = 5$

b. Do 52 + 12 - 4.5 + 6.1 -12 = 0 nên M(5; 1) thuộc (C).

Tiếp tuyến d của (C) tại M có vectơ pháp tuyến là $\overrightarrow{IM}(3; 4)$ $\vec{I M} (3; 4)$ và qua M(5; 1) nên có phương trình là:

3(x - 5) + 4(y - 1) = 0 hay 3x +4y -19 = 0.

Bài 7.35 trang 59

Cho elip (E): $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a>b>0).$ $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0) .$

a. Tìm các giao điểm A1, A2 của (E) với trục hoành và các giao điểm B1, B2 của (E) với trục tung. Tính A1A2 , B1B2.

b. Xét một điểm bất kì M(x0,y0) thuộc (E).

Chứng minh rằng, $b^{2}\leq x_{0}^{2}+y_{0}^{2}\leq a^{2} và b\leq OM\leq a.$ $b^{2} \leq x_{0}^{2} + y_{0}^{2} \leq a^{2} v à b \leq O M \leq a .$

Gợi ý đáp án

A1 thuộc trục hoành nên $y = 0 \Rightarrow \frac{x^{2}}{a^{2}}+\frac{0^{2}}{b^{2}}=1$ $y = 0 \Rightarrow \frac{x^{2}}{a^{2}} + \frac{0^{2}}{b^{2}} = 1$

$\Leftrightarrow x2 = a2.$ $\Leftrightarrow x 2 = a 2.$

Chọn A1 nằm bên trái trục Oy nên có hoành độ âm. Vậy tọa độ A1(-a; 0)
Chọn A2 nằm bên phải trục Oy nên có hoành độ dương. Vậy tọa độ A2(a; 0)

$\Rightarrow$ $\Rightarrow$ Độ dài A1A2 = 2a

B1 thuộc trục tung nên $x = 0 \Rightarrow \frac{0^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ $x = 0 \Rightarrow \frac{0^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

$\Leftrightarrow y2 = b2.$ $\Leftrightarrow y 2 = b 2.$

Chọn B1 nằm phía dưới trục Ox nên có tung độ âm. Vậy tọa độ B1(0; -b)
Chọn B2 nằm phía trên trục Ox nên có tung độ dương. Vậy tọa độ B2(0; b)

$\Rightarrow$ $\Rightarrow$ Độ dài B1B2 = 2b.

Giả sử $b^{2}\leq x_{0}^{2}+y_{0}^{2},$ $b^{2} \leq x_{0}^{2} + y_{0}^{2},$ chia cả hai vế cho b2 > 0 ta có:

$\Rightarrow 1\leq \frac{x_{0}^{2}}{b^{2}}+\frac{y_{0}^{2}}{b^{2}}\\\Leftrightarrow \frac{x_{0}^{2}}{a^{2}}+\frac{y_{0}^{2}}{b^{2}}\leq \frac{x_{0}^{2}}{b^{2}}+\frac{y_{0}^{2}}{b^{2}}\\\Leftrightarrow \frac{x_{0}^{2}}{a^{2}}\leq \frac{x_{0}^{2}}{b^{2}}$ $\Rightarrow 1 \leq \frac{x_{0}^{2}}{b^{2}} + \frac{y_{0}^{2}}{b^{2}} \Leftrightarrow \frac{x_{0}^{2}}{a^{2}} + \frac{y_{0}^{2}}{b^{2}} \leq \frac{x_{0}^{2}}{b^{2}} + \frac{y_{0}^{2}}{b^{2}} \Leftrightarrow \frac{x_{0}^{2}}{a^{2}} \leq \frac{x_{0}^{2}}{b^{2}}$

Luôn đúng vì a > b > 0.

Vậy $b^{2}\leq x_{0}^{2}+y_{0}^{2}$ $b^{2} \leq x_{0}^{2} + y_{0}^{2}$

Chứng minh tương tự có $x_{0}^{2}+y_{0}^{2}\leq a^{2}$ $x_{0}^{2} + y_{0}^{2} \leq a^{2}$

Vậy $b^{2}\leq x_{0}^{2}+y_{0}^{2}\leq a^{2}$ $b^{2} \leq x_{0}^{2} + y_{0}^{2} \leq a^{2}$

Theo chứng minh trên có: $b^{2}\leq x_{0}^{2}+y_{0}^{2}\leq a^{2}$ $b^{2} \leq x_{0}^{2} + y_{0}^{2} \leq a^{2}$

$\Rightarrow b\leq \sqrt{x_{0}^{2}+y_{0}^{2}}\leq a$ $\Rightarrow b \leq \sqrt{x_{0}^{2} + y_{0}^{2}} \leq a$

Mà $OM = \sqrt{x_{0}^{2}+y_{0}^{2}}$ $O M = \sqrt{x_{0}^{2} + y_{0}^{2}}$

Vậy $b\leq OM\leq a.$ $b \leq O M \leq a .$

Bài 7.36 trang 59

Cho hypebol có phương trình: $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$

a. Tìm các giao điểm A1, A2 của hypebol với trục hoành (hoành độ của A1 nhỏ hơn của A2).

b. Chứng minh rằng, nếu điểm M(x; y) thuộc nhánh nằm bên trái trục tung của hypebol thì $x\leq -a$ $x \leq - a$ , nếu điểm M(x; y) thuộc nhánh nằm bên phải trục tung của hypebol thì $x\geq a.$ $x \geq a .$

c. Tìm các điểm M1, M2 tương ứng thuộc cách nhánh bên trái, bên phải trục tung của hypebol để M1M2 nhỏ nhất.

Gợi ý đáp án

a. A1 thuộc trục hoành nên $y = 0 \Rightarrow \frac{x^{2}}{a^{2}}-\frac{0^{2}}{b^{2}}=1$ $y = 0 \Rightarrow \frac{x^{2}}{a^{2}} - \frac{0^{2}}{b^{2}} = 1$

$\Leftrightarrow x2 = a2.$ $\Leftrightarrow x 2 = a 2.$

Do hoành độ của A1 nhỏ hơn hoành độ của A2 nên A1(-a; 0) và A2(a; 0)

b. Ta chứng minh: $x2 \geq a2$ $x 2 \geq a 2$

Giả sử: $x2 \geq a2$ $x 2 \geq a 2$

$\Leftrightarrow \frac{x^{2}}{a^{2}}\geq 1$ $\Leftrightarrow \frac{x^{2}}{a^{2}} \geq 1$ (luôn đúng)

Luôn đúng vì $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\Leftrightarrow \frac{x^{2}}{a^{2}}=1+\frac{y^{2}}{b^{2}}\geq 1$ $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 \Leftrightarrow \frac{x^{2}}{a^{2}} = 1 + \frac{y^{2}}{b^{2}} \geq 1$

Nếu M thuộc nhánh bên trái trục tung thì x < 0 mà $x2 \geq a2$ $x 2 \geq a 2$ nên $x \leq -a.$ $x \leq - a .$
Nếu M thuộc nhánh bên phải trục tung thì x > 0 mà x² $\geq$ $\geq$ a² nên $x \geq a.$ $x \geq a .$

c. Gọi M1(x1; y1) thuộc nhánh bên trái nên x1 < 0, M2(x2; y2) thuộc nhánh bên phải nên x2 > 0

Theo b ta có: $x1 \leq -a$ $x 1 \leq - a$ và $x2 \geq a$ $x 2 \geq a$ nên $|x1| + |x2| \geq a + a = 2a.$ $| x 1 | + | x 2 | \geq a + a = 2 a .$

Do x1 < 0 và x2 > 0 nên x2 - x1 = | $x2| + |x1| \geq a + a = 2a.$ $x 2 | + | x 1 | \geq a + a = 2 a .$

Ta có: $M1M2 = \sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$ $M 1 M 2 = \sqrt{(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2}}$

Lại có: $(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}\geq \left ( |x_{2}|+|x_{1}| \right )^{2}+0\geq (2a)^{2}$ $(x_{2} - x_{1})^{2} + (y_{2} - y_{1})^{2} \geq {(| x_{2} | + | x_{1} |)}^{2} + 0 \geq (2 a)^{2}$

Nên $M1M2 \geq A1A2$ $M 1 M 2 \geq A 1 A 2$

Dấu "=" xảy ra khi và chỉ khi M1 trùng A1 và M2 trùng A2.

Vậy để M1M2 nhỏ nhất thì M1 trùng A1 và M2 trùng A2.

Bài 7.37 trang 59

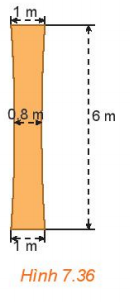
Một cột trụ hình hypebol (H.7.36), có chiều cao 6m, chỗ nhỏ nhất ở chính giữa và rộng 0,8 m, đỉnh cột và đáy cột đều rộng 1m. Tính độ rộng của cột ở độ cao 5 m (tính theo đơn vị mét và làm tròn tới hai chữ số sau dấu phẩy).

Gợi ý đáp án

Chọn hệ trục tọa độ sao cho gốc tọa độ trùng với điểm chính giữa hai cột, trục Oy đi qua điểm chính giữa, hai bên cột lần lượt nằm về hai phía của trục tung (như hình vẽ)

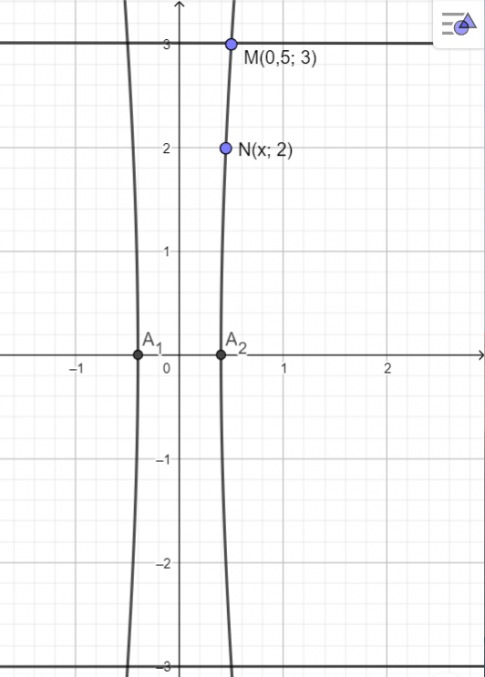
Phương trình hypebol (H) có dạng: $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$ $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$

(H) cắt trục hoành tại hai điểm A1(-0,4; 0) và A2(0,4; 0), nên a = 0,4.

(H) đi qua điểm có tọa độ M(0,5; 3) nên: $\frac{0,5^{2}}{0,4^{2}}-\frac{3^{2}}{b^{2}}=1$ $\frac{0, 5^{2}}{0, 4^{2}} - \frac{3^{2}}{b^{2}} = 1$

$\Rightarrow b2 = 16 \Rightarrow b =4$ $\Rightarrow b 2 = 16 \Rightarrow b = 4$ .

Vậy phương trình (H) là: $\frac{x^{2}}{0,16}-\frac{y^{2}}{16}=1$ $\frac{x^{2}}{0, 16} - \frac{y^{2}}{16} = 1$

Ở độ cao 5 m thì khoảng cách từ vị trí đó đến trục hoành là 2 m, tương ứng ta có tung độ điểm đó là $y = 2 \Rightarrow x2 = 0,2 \Leftrightarrow x \approx \pm 0,45$ $y = 2 \Rightarrow x 2 = 0, 2 \Leftrightarrow x \approx \pm 0, 45$

Suy ra độ rộng của cột là: 0,45.2 = 0,9 m.

Chia sẻ bởi:

Trịnh Thị Thanh

Tải về

Bài trước

Bài 22: Ba đường conic

Bài sau

Bài 23: Quy tắc đếm

Liên kết tải về

Toán 10 Bài tập cuối chương VII - Kết nối tri thức với cuộc sống 438,2 KB Tải về

Tìm thêm: Kết nối tri thức với cuộc sống Kết nối tri thức với cuộc sống Lớp 10

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!