Toán 10 Bài tập cuối chương I - Kết nối tri thức với cuộc sống Giải SGK Toán 10 trang 20 - Tập 1

Bài tập cuối chương 1 Toán 10 Kết nối tri thức là tài liệu vô cùng hữu ích, giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi bài 1.17→1.27 được nhanh chóng và dễ dàng hơn.

Giải Toán 10 Kết nối tri thức trang 20 tập 1 giúp các em nắm rõ kiến thức cơ bản trong bài học đầu tiên của Toán 10, tránh nhầm lẫn khi tiếp cận kiến thức mới. Toán 10 Kết nối tri thức Bài tập cuối chương 1 hướng dẫn cách giải các bước giải cụ thể để học sinh biết cách trình bày lời giải khoa học, chính xác. Giúp các em học sinh hệ thống lại nội dung, dễ dàng đối chiếu kết quả, từ đó khắc sâu kiến thức. Vậy sau đây là trọn bộ nội dung Giải Toán 10 Bài tập cuối chương 1, mời các bạn cùng theo dõi và tải tại đây.

Giải Toán 10 Bài tập cuối chương 1

Bài 1.17 trang 20

Câu nào sau đây không là mệnh đề?

A. Tam giác đều là tam giác có ba cạnh bằng nhau.

B. 3< 1

C. 4 - 5 = 1

D. Bạn học giỏi quá!

Gợi ý đáp án

A. “Tam giác đều là tam giác có ba cạnh bằng nhau.” Là một mệnh đề.

B. “3 < 1” là một mệnh đề.

C. “4 - 5 = 1” là một mệnh đề.

D. “Bạn học giỏi quá!” không là một mệnh đề.

Chọn đáp án D.

Bài 1.18 trang 20

Cho định lí: “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Mệnh đề nào sau đây là đúng?

A. Hai tam giác bằng nhau là điều kiện cần để diện tích của chúng bằng nhau.

B. Hai tam giác bằng nhau là điều kiện cần và đủ để diện tích của chúng bằng nhau

C. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau

D. Hai tam giác bằng nhau là điều kiện đủ để diện tích của chúng bằng nhau

Gợi ý đáp án

Chọn đáp án D.

Bài 1.19 trang 20

Mệnh đề nào sau đây là đúng?

\(A. \forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > - 1\)

\(B. \forall x \in \mathbb{R},{x^2} > 1 \Rightarrow x > 1\)

\(C. \forall x \in \mathbb{R},x > - 1 \Rightarrow {x^2} > 1\)

\(D. \forall x \in \mathbb{R},x > 1 \Rightarrow {x^2} > 1\)

Gợi ý đáp án

Chọn đáp án D

Bài 1.20 trang 20

Cho tập hợp A = {a;b;c}. Tập A có bao nhiêu tập con?

A. 4

B. 6

C. 8

D. 10

Gợi ý đáp án

Chọn đáp án C.

Bài 1.21 trang 20

Cho tập hợp A,B được mình họa bằng biểu đồ Ven như hình bên. Phần tô màu xám trong hình là biểu diễn của tập hợp nào sau đây?

\(A. A \cap B\)

\(B. A\;{\rm{\backslash }}\;B\)

\(C. A \cup B\)

\(D. B\;{\rm{\backslash }}\;A\)

Gợi ý đáp án

Phần màu xám là phần giao nhau giữa tập hợp A và tập hợp B: vừa thuộc A, vừa thuộc B.

Do đó phần màu xám là A \cap B

Bài 1.22 trang 20

Biểu diễn các tập hợp sau bằng biểu đồ Ven:

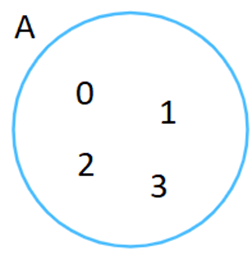
\(a) A = \left\{ {0;1;2;3} \right\}\)

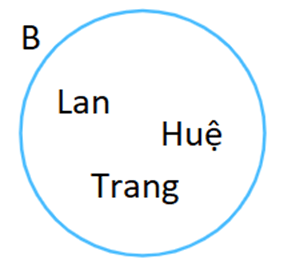
b) B = {Lan; Huệ; Trang}

Gợi ý đáp án

a) A =\(\left\{ {0;1;2;3} \right\}\). Biểu đồ Ven:

b) B = {Lan; Huệ; Trang}. Biểu đồ Ven:

Bài 1.23 trang 20

Phần không bị gạch trên trục số dưới đây biểu diễn tập hợp số nào?

Phương pháp giải 

- Tập hợp không chưa phần tử nào được gọi là tập rỗng, kí hiệu là: ∅

- Giao của hai tập hợp S và T:

S ⋂ T = {x | x ∈ S và x ∈ T}

- Hợp của hai tập hợp S và T:

S ∪ T = {x | x ∈ S hoặc x ∈ T}

- Hiệu của hai tập hợp S và T:

S \ T = {x | x ∈ S và x ∉ T}

Gợi ý đáp án

Ta có:

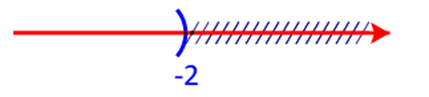
Biểu diễn khoảng \(\left( { - \infty ; - 2} \right)\)

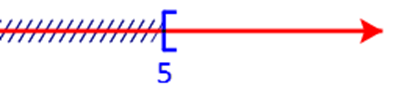
Biểu diễn nửa khoảng \([5; + \infty )\)

Vậy phần không bị gạch trên trục số là \(\left( { - \infty ; - 2} \right) \cup [5; + \infty )\)

Bài 1.24 trang 21

Cho \(A = \left\{ {x \in \mathbb{Z}|\;x < 7} \right\}, \,B = \left\{ {1;2;3;6;7;8} \right\}.\) Xác định các tập hợp sau:

\(A \cup B,\;A \cap B,\;A\,{\rm{\backslash }}\,B\)

Phương pháp giải 

- Tập hợp không chưa phần tử nào được gọi là tập rỗng, kí hiệu là: ∅

- Giao của hai tập hợp S và T:

S ⋂ T = {x | x ∈ S và x ∈ T}

- Hợp của hai tập hợp S và T:

S ∪ T = {x | x ∈ S hoặc x ∈ T}

- Hiệu của hai tập hợp S và T:

S \ T = {x | x ∈ S và x ∉ T}

Gợi ý đáp án

\(A = \left\{ {6;5;4;3;2;1;0; - 1; - 2;...} \right\}\)

\(\,B = \left\{ {1;2;3;6;7;8} \right\}\)

Vậy

\(A \cap B = \left\{ {1;2;3;6} \right\}\)

\(A \cup B = \left\{ {8;7;6;5;4;3;2;1;0; - 1; - 2;...} \right\} = \left\{ {x \in \mathbb{Z}|\;x < 9} \right\}\)

\(A\;{\rm{\backslash }}\;B = \left\{ {5;4;0; - 1; - 2; - 3;...} \right\}\)

Bài 1.25 trang 21

Cho hai tập hợp A = [-2; 3] và B = (1; +∞). Xác định các tập hợp sau: A ∩ B; B \ A; C_ℝB.

Gợi ý đáp án

Cách 1

Ta có:

A ∩ B = [1;3];

B \ A = (3; +∞);

C_ℝB=(−∞;1]

Cách 2:

Ta có:

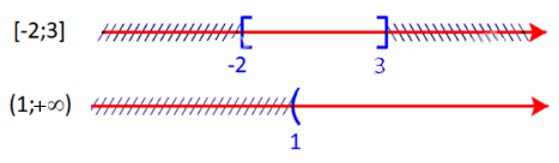
Do đó:

+ Giao của hai tập hợp A và B là: A ∩ B = [– 2; 3] ∩ (1; + ∞) = (1; 3].

+ Hiệu của B và A là: B \ A = (1; + ∞) \ [– 2; 3] = (3; + ∞).

+ Phần bù của B trong ℝ là: C_ℝB = ℝ \ B = ℝ \ (1; + ∞) = (– ∞; 1].

Bài 1.26 trang 21

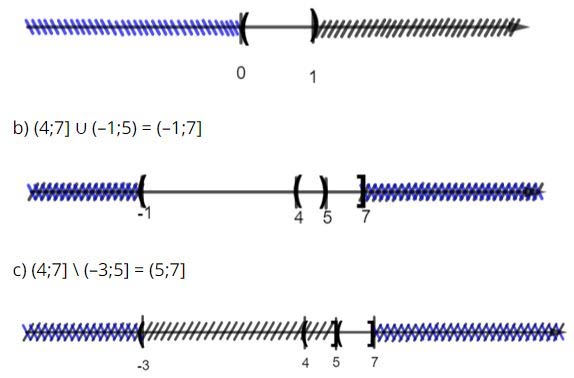
Xác định các tập hợp sau và biểu diễn chúng trên trục số.

a) (–∞;1) ∩ (0; +∞);

b) (4;7] ∪ (–1;5);

c) (4;7] \ (–3;5].

Phương pháp giải

- Tập hợp không chưa phần tử nào được gọi là tập rỗng, kí hiệu là: ∅

- Giao của hai tập hợp S và T:

S ⋂ T = {x | x ∈ S và x ∈ T}

- Hợp của hai tập hợp S và T:

S ∪ T = {x | x ∈ S hoặc x ∈ T}

- Hiệu của hai tập hợp S và T:

S \ T = {x | x ∈ S và x ∉ T}

Gợi ý đáp án

a) (–∞;1) ∩ (0; +∞) = (0;1)

Biểu diễn trên trục số, ta được:

Bài 1.27 trang 21

Một cuộc khảo sát về khách du lịch thăm vịnh Hạ Long cho thấy trong 1 410 khách du lịch được phỏng vấn có 789 khách du lịch đến thăm động Thiên Cung, 690 khách du lịch đến thăm đảo Titop. Toàn bộ khách được phỏng vẫn đã đến ít nhất một trong hai địa điểm trên. Hỏi có bao nhiêu khách du lịch vừa đến thăm động Thiên Cung vừa đến thăm đảo Titop ở Vịnh Hạ Long?

Phương pháp giải 

- Ta có công thức:

n(A ∪ B) = n(A) + n(B) - n(A ⋂ B)

- Giao của hai tập hợp S và T:

S ⋂ T = {x | x ∈ S và x ∈ T}

- Hợp của hai tập hợp S và T:

S ∪ T = {x | x ∈ S hoặc x ∈ T}

- Hiệu của hai tập hợp S và T:

S \ T = {x | x ∈ S và x ∉ T}

Gợi ý đáp án

Số khách du lịch vừa đến thăm động Thiên Cung vừa đến thăm đảo Titop là:

789 + 690 – 1 410 = 69 (khách)

Vậy có 69 khách du lịch vừa đến thăm động Thiên Cung vừa đến thăm đảo Titop.