Toán 10 Bài 23: Quy tắc đếm Giải SGK Toán 10 trang 65 - Tập 2 sách Kết nối tri thức với cuộc sống

Giải Toán lớp 10 trang 65 tập 2 Kết nối tri thức với cuộc sống giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi bài tập trong SGK bài 23 Quy tắc đếm thuộc Chương 8 Đại số tổ hợp.

Toán 10 Kết nối tri thức trang 65 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 10. Giải Toán lớp 10 trang 65 Kết nối tri thức sẽ là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn. Vậy sau đây là trọn bộ bài giải Toán 10 bài 23: Quy tắc đếm mời các bạn cùng theo dõi.

Giải Toán 10 Bài 23: Quy tắc đếm

Trả lời câu hỏi Hoạt động Toán 10 Bài 23

Giải Toán 10 trang 65 Kết nối tri thức Tập 2

Trả lời câu hỏi Hoạt động Toán 10 Bài 23

Hoạt động 1

Chọn chuyến đi (H.8.1)

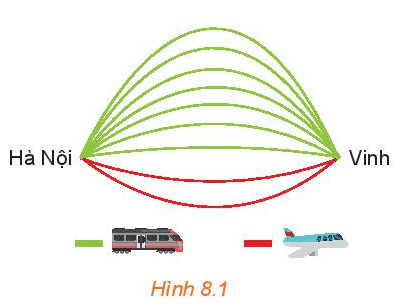
Từ Hà Nội vào Vinh mỗi ngày có 7 chuyến tàu hỏa và 2 chuyến máy bay. Bạn An muốn ngày Chủ nhật này đi từ Hà Nội vào Vinh bằng tàu hỏa hoặc máy bay. Hỏi bạn An có bao nhiêu cách chọn chuyến đi?

Gợi ý đáp án

Bạn An có thể chọn đi tàu hỏa hoặc đi máy bay.

+) Vì có 7 chuyến tàu hỏa mỗi ngày, nên An có thể chọn 1 chuyến bất kì trong 7 chuyến đó để đi. Do đó An có 7 cách chọn tàu hỏa.

+) Vì có 2 chuyến máy nay mỗi ngày, nên An có thể chọn 1 chuyến bất kì trong 2 chuyến đó để đi. Do đó An có 2 cách chọn máy bay.

Vì tàu hỏa và máy bay là khác nhau nên An có 7 + 2 = 9 (cách chọn).

Vậy bạn An có 9 cách chọn chuyến đi.

Hoạt động 2

Chọn vé tàu (H.8.2)

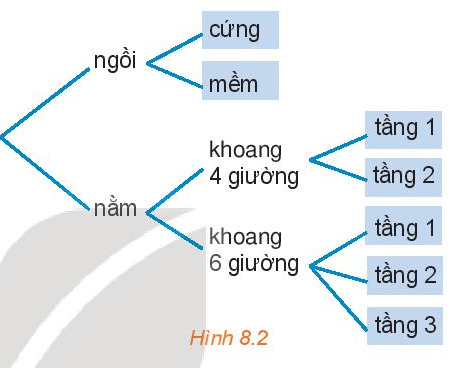
Bạn An đã quyết định mua vé tàu đi từ Hà Nội vào Vinh trên chuyến tàu SE7. Trên tàu có các toa ghế ngồi và các toa giường nằm. Toa ngồi có hai loại vé: ngồi cứng và ngồi mềm. Toa nằm có loại khoang 4 giường và khoang 6 giường. Khoang 4 giường có hai loại vé: tầng 1 và tầng 2, khoang 6 giường có ba loại vé: tầng 1, tầng 2 và tầng 3. Hỏi:

a) Có bao nhiêu loại vé ghế ngồi và bao nhiêu loại vé giường nằm?

b) Có bao nhiêu loại vé để bạn An lựa chọn?

Gợi ý đáp án

a) Toa ngồi có hai loại vé: ngồi cứng và ngồi mềm nên số loại vé ghế ngồi là 2.

Toa nằm có loại khoang 4 giường và khoang 6 giường.

+ Khoang 4 giường có 2 loại vé: tầng 1 và tầng 2.

+ Khoang 6 giường có 3 loại vé: tầng 1, tầng 2 và tầng 3.

Số loại vé giường nằm là: 2 + 3 = 5.

Vậy có 2 loại vé ghế ngồi và 5 loại vé giường nằm.

b) An chọn loại vé ghế ngồi: có 2 cách chọn.

An chọn loại vé giường nằm: có 5 cách chọn.

Vậy số loại vé để An lựa chọn: 2 + 5 = 7 (cách chọn).

Giải Toán 10 trang 65 Kết nối tri thức Tập 2

Bài 8.1 trang 65

Trên giá sách có 8 cuốn truyện ngắn, 7 cuốn tiểu thuyết và 5 tập thơ (tất cả đều khác nhau). Vẽ sơ đồ hình cây minh hoạ và cho biết bạn Phong có bao nhiêu cách chọn một cuốn để đọc vào ngày cuối tuần.

Gợi ý đáp án

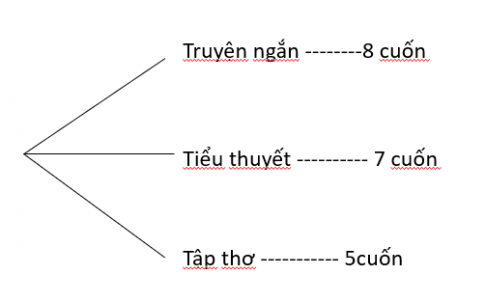
Số cách chọn một cuốn sách để đọc là: 8 + 7 + 5 = 20 cuốn.

Bài 8.2 trang 65

Một người gieo đồng xu hai mặt, sau mỗi lần gieo thì ghi lại kết quả là sấp hay ngửa. Hỏi nếu người đó gieo 3 lần thì có thể có bao nhiêu khả năng xảy ra?

Gợi ý đáp án

• Gieo lần 1 thì có thể xuất hiện mặt sấp hoặc ngửa nên số khả năng xảy ra là: 2.
• Gieo lần 2 tương tự lần 1, số khả năng là: 2.
• Gieo lần 3 tương tự như trên, số khả năng là: 2.

\(\Rightarrow\) Vậy sau gieo 3 lần, số khả năng xảy ra là: 2.2.2 = 8.

Bài 8.3 trang 65

Ở một loài thực vật, A là gen trội quy định tính trạng hoa kép, a là gen lặn quy định tính trạng hoa đơn.

a. Sự tổ hợp giữa hai gen trên tạo ra mấy kiểu gen? Viết các kiểu gen đó.

b. Khi giao phối ngẫu nhiên, có bao nhiêu kiểu giao phối khác nhau từ các kiểu gen đó?

Gợi ý đáp án

a. Tổ hợp tạo 3 kiểu gen: AA, Aa, aa.

b. Khi giao phiếu ngẫu nhiên thì AA có thể tạo với AA, Aa, aa.

Suy ra có các kiểu: AA ×AA; AA×Aa; AA×aa; Aa×Aa; Aa×aa; aa×aa

Có 6 kiểu giao phối khác nhau từ các kiểu gen đó.

Bài 8.4 trang 65

Có bao nhiêu số tự nhiên

a. Có 3 chữ số khác nhau?

b. Là số lẻ có 3 chữ số khác nhau?

c. Là số có 3 chữ số và chia hết cho 5?

d. Là số có 3 chữ số khác nhau và chia hết cho 5?

Gợi ý đáp án

a. Gọi số tự nhiên cần lập có dạng: \(\overline{abc},\) với a, b, c thuộc tập hợp số A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, (\(a \neq 0, a\neq b\neq c\)).

• Chọn số a có 9 cách, do \(a \neq 0.\)
• Chọn b có 9 cách từ tập A\{a}
• Chọn c có 8 cách từ tập A\{a; b}

Số các số thõa mãn bài toán là: 9.9.8 = 648 số.

b. Gọi số tự nhiên cần lập có dạng: \overline{abc}, với a, b, c thuộc tập hợp số A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, (\(a \neq 0, a\neq b\neq c\)).

Để \overline{abc} là số lẻ thì c thuộc tập hợp {1; 3; 5; 7; 9},

• Chọn c có 5 cách từ tập {1; 3; 5; 7; 9},
• Chọn a có 8 cách từ tập A\{c; 0}
• Chọn b có 8 cách từ tập A\{c; a}

Số các số thỏa mãn bài toán là: 5.8.8 = 320 số.

c. Gọi số tự nhiên cần lập có dạng: \(\overline{abc}\), với a, b, c thuộc tập hợp số A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, (\(a \neq 0\))

Để \(\overline{abc}\) chia hết cho 5 thì c thuộc tập hợp {0; 5},

• Chọn c có 2 cách từ tập {0; 5},
• Chọn a có 9 cách từ tập A\{0}
• Chọn b có 10 cách từ tập A

Vậy số các số 3 chữ số mà chia hết cho 5 là: 2.9.10 = 180 số.

d. Gọi số tự nhiên cần lập có dạng: \(\overline{abc},\) với a, b, c thuộc tập hợp số A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, (\(a \neq 0, a\neq b\neq c)\).

Để \overline{abc} chia hết cho 5 thì c thuộc tập hợp {0; 5},

• Nếu c = 0 thì: chọn a có 9 cách, chọn b có 8 cách

\(\Rightarrow\) Số các số 3 chữ số khác nhau mà tận cùng là 0 là: 9.8 = 72 số.

• Nếu c = 5 thì: chọn a có 8 cách, chọn b có 8 cách

\(\Rightarrow\)Số các số 3 chữ số khác nhau mà tận cùng là 5 là: 8.8 = 64 số.

Vậy số các số 3 chữ số khác nhau mà chia hết cho 5 là: 72+ 64 = 136 số.

Bài 8.5 trang 65

a. Mật khẩu của chương trình máy tính quy định gồm 3 kí tự, mỗi kỉ tự là một chữ số. Hỏi có thể tạo được bao nhiêu mật khẩu khác nhau?

b. Nếu chương trình máy tính quy định mới mật khẩu vẫn gồm 3 kí tự, nhưng kí tự đầu tiên phải là một chứ cái in hoa trong bảng chữ cái tiếng Anh gồm 26 chữ (từ A đến Z) và 2 kí tự sau là các chữ số (từ 0 đến 9). Hỏi quy định mới có thể tạo được nhiều hơn quy định cũ bao nhiêu mật khẩu khác nhau?

Gợi ý đáp án

a. Gọi số tự nhiên cần lập có dạng: \overline{abc}, với a, b, c thuộc tập hợp số A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

• Chọn a có 10 cách từ tập A.
• Chọn b có 10 cách từ tập A.
• Chọn c có 10 cách từ tập A.

Vậy có thể tạo được số mật khẩu là: 10.10.10 = 1000 mật khẩu.

b. Chọn kí tự đầu từ tập 26 chữ từ A đến Z thì có 26 cách chọn,

• Chọn kí tự thứ hai là chữ số có 10 cách chọn,
• Chọn kí tự thứ ba là chữ số có 10 cách chọn.

\(\Rightarrow\)Số cách tạo mật khẩu mới là: 26.10.10 = 2600 mật khẩu.

Vậy có thể tạo được nhiều hơn quy định cũ số mật khẩu là: 2600 - 1000 = 1600 mật khẩu.