Định luật Cu lông Công thức định luật Cu lông

Tải về Bình luận

Định luật Cu lông ra đời đã chứng minh được rằng khi khoảng cách càng xa, lực tác dụng giữa hai điện tích điểm càng giảm. Vậy công thức Cu lông là gì?

Công thức định luật Cu lông giúp các bạn học sinh lớp 11 nhanh chóng nắm được toàn bộ kiến thức về phát biểu định luật, công thức mở rộng, điện ích là gì và kỹ năng giải bài tập về điện tích Cu lông. Từ đó nhanh chóng giải được các bài tập Vật lí 11. Vậy sau đây là nội dung chi tiết tài liệu Định luật Cu lông, mời các bạn cùng theo dõi tại đây.

1. Điện tích là gì?

Vật bị nhiễm điện còn gọi là vật mang điện, vật tích điện hay vật chứa điện tích.

2. Điện tích điểm là gì?

- Điện tích điểm là một vật tích điện có kích thước rất nhỏ so với khoảng cách tới điểm mà ta xét. Điện tích điểm là điện tích được coi như tập trung tại một điểm.

3. Tương tác điện. Hai loại điện tích

- Các điện tích hoặc đẩy nhau, hoặc hút nhau (Hình 1.1). Sự đẩy nhau hay hút nhau giữa các điện tích đó là tương tác điện.

- Có hai loại điện tích là điện tích dương (+) và điện tích âm (-).

Các điện tích cùng loại (cùng dấu) thì đẩy nhau.
Các điện tích khác loại (khác dấu) thì hút nhau.

- Hai lực tác dụng vào hai điện tích là hai lực trực đối, cùng phương, ngược chiều, độ lớn bằng nhau và đặt vào hai điện tích.

4. Định luật Cu lông

Định luật Cu-lông: Lực hút hay đẩy giữa hai điện tích điểm đặt trong chân không có phương trùng với đường thẳng nối hai điện tích điểm đó, có độ lớn tỉ lệ thuận với tích độ lớn của hai điện tích và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.

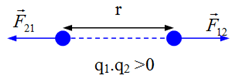
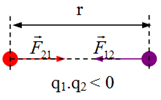
Công thức định luật Cu lông

$\mathrm{F}=\mathrm{k} \frac{\left|\mathrm{q}_{1} \mathrm{q}_{2}\right|}{\mathrm{r}^{2}}$ $\mathrm{F}=\mathrm{k} \frac{\left|\mathrm{q}_{1} \mathrm{q}_{2}\right|}{\mathrm{r}^{2}}$

Trong đó:

F: lực tương tác (F)
k = 9.10⁹: hệ số tỉ lệ (Nm²/C²)
q₁, q₂: điện tích của 2 điện tích (C)
r: khoảng cách giữa 2 điện tích (m)

- Điện môi là môi trường cách điện. Hằng số điện môi ε đặc trưng cho tính chất điện của một chất cách điện. Khi đặt điện tích trong điện môi, lực tương tác sẽ nhỏ đi ε so với đặt trong chân không.

$\mathrm{F}=\mathrm{k} \frac{\left|\mathrm{q}_{1} \mathrm{q}_{2}\right|}{\mathrm{er}^{2}}$ $\mathrm{F}=\mathrm{k} \frac{\left|\mathrm{q}_{1} \mathrm{q}_{2}\right|}{\mathrm{er}^{2}}$

5. Kỹ năng giải bài tập

Dạng 1: Tính lực tương tác, điện tích hay khoảng cách giữa 2 điện tích.

Bước 1. Áp dụng định luật Cu-lông viết phương trình.

Bước 2. Giải phương trình

Bước 3. Kết luận.

Dạng 2: Tính lực tổng hợp tác dụng lên điện tích q

Bước 1. Xác định các lực tác dụng lên điện tích, biểu diễn chúng bằng các vecto có gốc là điện tích q.

Bước 2. Từ đó áp dụng nguyên lý chồng chất lực điện để tìm lực tổng hợp. Tính lực theo phương pháp hình học hoặc tổng hợp lực theo quy tắc hình bình hành.

Bước 3. Kết luận.

Chia sẻ bởi: