Toán 9 Bài 4: Hình quạt tròn và hình vành khuyên Giải Toán 9 Chân trời sáng tạo tập 1 trang 98 → 102

Giải Toán 9 Bài 4: Hình quạt tròn và hình vành khuyên là tài liệu vô cùng hữu ích giúp các em học sinh lớp 9 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 9 Chân trời sáng tạo tập 1 trang 98, 99, 100, 101, 102.

Giải bài tập Toán 9 Chân trời sáng tạo tập 1 trang 99 → 102 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 4 Chương V: Đường tròn - Phần Hình học và đo lường - Hình học phẳng. Mời thầy cô và các em theo dõi bài viết dưới đây của Download.vn:

Giải Toán 9 Chân trời sáng tạo Tập 1 trang 102

Bài 1

Tính độ dài các cung 30^o; 90^o; 120^o của đường tròn (O; 6 cm)

Hướng dẫn giải:

Cung 30^o, bán kính R = 6 cm có độ dài là:

\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .6.30}}{{180}} = \pi \approx 3,14\) cm

Cung 90⁰, bán kính R = 6 cm có độ dài là:

\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .6.90}}{{180}} = 3\pi\approx9,42\) cm

Cung 120^o, bán kính R = 6 cm có độ dài là:

\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .6.120}}{{180}} = 4\pi \approx12,57\) cm

Bài 2

Tính diện tích hình quạt tròn ứng với cung số đo lần lượt là 30^o; 90^o; 120^o của hình tròn (O; 12 cm).

Hướng dẫn giải:

Diện tích của hình quạt tròn bán kính R = 12 cm, ứng với cung 30^o là:

\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.12}^2}.30}}{{360}} =12\pi \approx 37,70\) (cm²)

Diện tích của hình quạt tròn bán kính R = 12 cm, ứng với cung 90^o là:

\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.12}^2}.90}}{{360}} =36\pi \approx 113,1\) (cm²)

Diện tích của hình quạt tròn bán kính R = 12 cm, ứng với cung 120^o là:

\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.12}^2}.120}}{{360}} =48\pi\approx 150,8\) (cm²)

Bài 3

Tính diện tích hình quạt tròn ứng với cung có độ dài lần lượt là 8 cm, 15 cm của hình tròn (O; 5 cm).

Hướng dẫn giải:

Ta có: \(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{R.\pi Rn}}{{2.180}} =\frac{{Rl}}{{2}}\)

Diện tích của hình quạt tròn bán kính R = 5 cm, ứng với cung có độ dài 8 cm có diện tích là:

\(S = \frac{{R.l}}{2} = \frac{{5.8}}{2} = 20\) (cm²)

Diện tích của hình quạt tròn bán kính R = 5 cm, ứng với cung có độ dài 15 cm có diện tích là:

\(S = \frac{{R.l}}{2} = \frac{{5.15}}{2} = 37,5\) (cm²)

Bài 4

Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 9 cm) và (O; 12 cm).

Hướng dẫn giải:

Hình vành khuyên giới hạn bởi (O; 9 cm) và (O; 12 cm) có diện tích là:

S = π(R² – r²) = π.(12² – 9²) = 63π ≈ 197,92 (cm²)

Bài 5

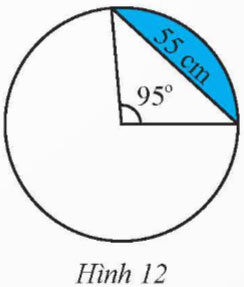
Tính diện tích hình viên phân giới hạn bởi dây cung có độ dài là 55 cm và cung có số đo là 95° (Hình 12).

Bài 6

Một máy kéo nông nghiệp có đường kính bánh xe sau là 124 cm và đường kính bánh xe trước là 80 cm. Hỏi khi bánh xe sau lăn được 20 vòng thì bánh xe trước lăn được bao nhiêu vòng?

Hướng dẫn giải:

Chu vi của bánh xe sau là:

π . d = 124π (cm)

Chu vi của bánh xe trước là:

π . d' = 80π (cm)

Sau khi lăn được 20 vòng thì bánh xe sau đi được quãng đường là:

124π . 20 = 2 480π (cm)

Khi đó, bánh xe trước lăn được số vòng là:

2 480π : 80π = 31 (vòng)

Bài 7

Thành phố Đà Lạt nằm vào khoảng 11^o 58' vĩ độ Bắc. Mỗi vòng kinh tuyến của Trái Đất dài khoảng 40 000 km. Hãy tính độ dài cung kinh tuyến từ Đà Lạt đến xích đạo.

(Nguồn: https://vi.wikipedia.org/wiki/Đà-Lạt.)

Hướng dẫn giải:

Ta có mỗi vòng kinh tuyến của Trái Đất dài khoảng 40 000 km, nghĩa là chu vi một vòng kinh tuyến khoảng 40 000 km.

Do đó bán kính của Trái Đất là:

\(R=\frac{C}{2\pi}\approx\frac{20\ 000}{\pi}\) (km)

Đổi \(11^{\circ} 58'=\left(11+\frac{58}{60}\right)^{\circ} =\left(\frac{359}{30}\right) ^{\circ}\)

Độ dài cung kinh tuyến từ Đà Lạt đến xích đạo là:

\(l = \frac{{\pi Rn}}{{180}} = \frac{{ \pi.\frac{20\ 000}{\pi} .\left (\frac{359}{30} \right ) }}{{180}} \approx 1329,63\) (km)