Tiệm cận ngang của đồ thị hàm số Tiệm cận ngang

Tải về Bình luận

Tiệm cận ngang là gì? Tiệm cận ngang của đồ thị hàm số là đường thẳng như thế nào? Các công thức và các dạng bài tập Tiệm cận ngang. Mời các bạn cùng theo dõi bài viết dưới đây của Download.vn.

Đường tiệm cận ngang của một hàm số là một đường nằm ngang mà đồ thị của hàm số có vẻ trùng nhưng nó không thực sự trùng. Đường tiệm cận ngang được sử dụng để xác định giá trị cuối cùng của hàm. Hi vọng qua tài liệu này giúp các bạn lớp 12 học tập chủ động, nâng cao kiến thức để đạt kết quả cao trong kì thi THPT Quốc gia sắp tới. Bên cạnh đó các bạn xem thêm: tiệm cận đứng, Tìm m để hàm số đồng biến, nghịch biến trên R, Bài tập phương trình phức, Bài tập thể tích khối chóp có một cạnh bên vuông góc với đáy, 572 câu trắc nghiệm chuyên đề Hàm số nâng cao.

Tiệm cận ngang của đồ thị hàm số

1. Tiệm cận ngang
2. Cách tìm tiệm cận ngang của đồ thị hàm số
3. Bài tập tìm tiệm cận ngang của đồ thị hàm số

1. Tiệm cận ngang

- Cho đồ thị hàm số $y = f\left( x \right)$ $y = f\left( x \right)$ có tập xác định D.

- Nếu $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}$ $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = {y_0}$ hoặc $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}$ $\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = {y_0}$ thì đường thẳng $y = {y_0}$ $y = {y_0}$ được gọi là tiệm cận ngang của đồ thị hàm số.

2. Cách tìm tiệm cận ngang của đồ thị hàm số

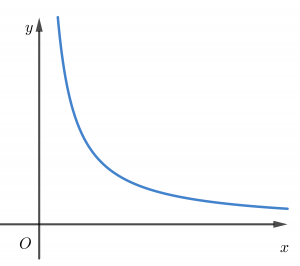
Trước tiên cần lưu ý rằng chúng ta hay nhầm lẫn là tiệm cận ngang của hàm số. Hàm số không có tιệm cận ngang mà đồ thị hàm số mới có tιệm cận ngang. Lưu ý thứ hai là tiệm cận đứng và tiệm cận ngang cách xác định khác nhau.

Cách xác định tiệm cận ngang của đồ thị hàm số bao gồm các bước sau:

Phương pháp giải

Bước 1. Tìm tập xác định của hàm số.

Bước 2. Tính các giới hạn của hàm số đó tại vô cực (nếu có). Từ đó xác định đường tιệm cận ngang.

Công thức tính tiệm cận ngang của hàm phân thức hữu tỉ:

Hàm số		Tiệm cận ngang
$y = \frac{{{a_0}{x^m} + {a_1}{x^{m - 1}} + ... + {a_m}}}{{{b_0}{x^n} + {b_1}{x^{n - 1}} + ... + {b_m}}}$ $y = \frac{{{a_0}{x^m} + {a_1}{x^{m - 1}} + ... + {a_m}}}{{{b_0}{x^n} + {b_1}{x^{n - 1}} + ... + {b_m}}}$ ${a_0} \ne 0,{b_0} \ne 0;m \geqslant 1;n \geqslant 1;m,n \in \mathbb{Z}$ ${a_0} \ne 0,{b_0} \ne 0;m \geqslant 1;n \geqslant 1;m,n \in \mathbb{Z}$	m = n	$y = \frac{{{a_0}}}{{{b_0}}}$ $y = \frac{{{a_0}}}{{{b_0}}}$
	m > n	Không có tiệm cận ngang
	m < n	y = 0

Công thức tính tiệm cận ngang của hàm phân thức vô tỷ:

Hàm số		Tiệm cận ngang
$y = \frac{{ax + b}}{{\sqrt {c{x^2} + dx + e} }}$ $y = \frac{{ax + b}}{{\sqrt {c{x^2} + dx + e} }}$	c < 0	Không có tiệm cận ngang
$a,c \ne 0$ $a,c \ne 0$	c > 0	$y = \pm \frac{a}{{\sqrt c }}$ $y = \pm \frac{a}{{\sqrt c }}$

3. Bài tập tìm tiệm cận ngang của đồ thị hàm số

Câu 1: Tìm tiệm cận ngang của đồ thị hàm số: $y = \frac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}}$ $y = \frac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}}$

Hướng dẫn giải

$\begin{matrix} \mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}} = \dfrac{3}{2} \hfill \\ \mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}} = \dfrac{{ - 1}}{2} \hfill \\ \end{matrix}$ $\begin{matrix} \mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}} = \dfrac{3}{2} \hfill \\ \mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{x + \sqrt {4{x^2} - 3} }}{{2x + 3}} = \dfrac{{ - 1}}{2} \hfill \\ \end{matrix}$

Vậy $y = \frac{3}{2};y = \frac{{ - 1}}{2}$ $y = \frac{3}{2};y = \frac{{ - 1}}{2}$ là tiệm cận ngang của đồ thị hàm số.

Câu 2: Cho hàm số $y = \frac{{x - 1}}{{\sqrt {{x^2} - 3x + 2} }}$ $y = \frac{{x - 1}}{{\sqrt {{x^2} - 3x + 2} }}$ có đồ thị (C). Tìm khẳng định đúng trong các khẳng định sau:

A. (C) có đúng một tiệm cận ngang y = 1

B. (C) có đúng một tiệm cận ngang y = -1

C. (C) không có tiệm cận ngang

D. (C) có hai tiệm cận ngang là y = 1 và y = -1

Hướng dẫn giải

$\begin{matrix} \mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{1 - \frac{1}{x}}}{{\sqrt {1 - \dfrac{3}{x} + \dfrac{2}{{{x^2}}}} }} = 1 \hfill \\ \mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{1 - \dfrac{1}{x}}}{{\sqrt {1 - \dfrac{3}{x} + \dfrac{2}{{{x^2}}}} }} = - 1 \hfill \\ \end{matrix}$ $\begin{matrix} \mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{1 - \frac{1}{x}}}{{\sqrt {1 - \dfrac{3}{x} + \dfrac{2}{{{x^2}}}} }} = 1 \hfill \\ \mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{1 - \dfrac{1}{x}}}{{\sqrt {1 - \dfrac{3}{x} + \dfrac{2}{{{x^2}}}} }} = - 1 \hfill \\ \end{matrix}$

Vậy y =1 và y = -1 là hai tiệm cận ngang của đồ thị hàm số (C)

Đáp án D

Câu 3: Cho đồ thị hàm số $y = \sqrt {m{x^2} + 2x} - x$ $y = \sqrt {m{x^2} + 2x} - x$. Tìm tất cả giá trị tham số m để đồ thị hàm số có tiệm cận ngang.

A. $m > 0$	B. $m = - 2$
C. $m = \pm 1$ $m = \pm 1$	D. $m = \left\{ {1; - 2} \right\}$ $m = \left\{ {1; - 2} \right\}$

Hướng dẫn giải

Ta có: $y = \sqrt {m{x^2} + 2x} - x = \frac{{m{x^2} + 2x - {x^2}}}{{\sqrt {m{x^2} + 2x} + x}} = \frac{{\left( {m - 1} \right){x^2} + 2x}}{{\sqrt {m{x^2} + 2x} + x}}$ $y = \sqrt {m{x^2} + 2x} - x = \frac{{m{x^2} + 2x - {x^2}}}{{\sqrt {m{x^2} + 2x} + x}} = \frac{{\left( {m - 1} \right){x^2} + 2x}}{{\sqrt {m{x^2} + 2x} + x}}$

Đồ thị hàm số có tiệm cận ngang khi và chỉ khi bậc của tử bé hơn bậc của mẫu và tồn tại

$\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {m - 1 = 0} \end{array} \Leftrightarrow m = 1} \right.$ $\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {m > 0} \\ {m - 1 = 0} \end{array} \Leftrightarrow m = 1} \right.$

Đáp án A

Chia sẻ bởi: