™
Download.vn Học tập Công thức toán

Tóm tắt công thức Toán cấp 2 Tổng hợp các công thức Toán THCS đầy đủ nhất

Tải về Bình luận
  • 198

Trọn bộ công thức Toán THCS tóm tắt một số công thức trọng tâm của phần Hình học và Đại số có trong chương trình Toán lớp 6, 7, 8, 9.

Tóm tắt công thức Toán cấp 2 giúp các bạn vừa nắm vững và vận dụng kiến thức, vừa có cái nhìn bao quát toàn bộ chương trình Toán trải dài từ lớp 6 đến lớp 9 về các kiến thức như: điểm, đường thẳng, ba điểm thẳng hàng, đường thẳng trùng nhau, cắt nhau, song song, phương trình bậc nhất, phương trình bậc hai, hằng đẳng thức, phương trình trùng phương, số hữu tỉ ... Vậy dưới đây là trọn bộ công thức toán THCS mời các bạn cùng theo dõi nhé.

Trọn bộ công thức Toán cấp 2

1. Điểm - Đường thẳng

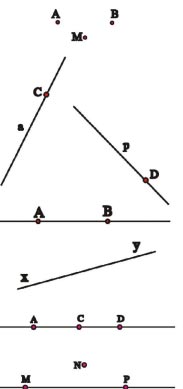
- Người ta dùng các chữ cái in hoa A, B, C, để đặt tên cho điểm

- Bất cứ hình nào cũng là một tập hợp các điểm. Một điểm cũng là một hình.

- Người ta dùng các chữ cái thường a, b, c, ...... m, p, ...để đặt tên cho các đường thẳng (hoặc dùng hai chữ cái in hoa hoặc dùng hai chữ cái thường, ví dụ đường thẳng AB, xy, ...)

- Điểm C thuộc đường thẳng a (điểm C nằm trên đường thẳng a hoặc đường thẳng a đi qua điểm C ), kí hiệu là:\mathrm{C} \in \mathrm{a}C∈a

- Điểm M không thuộc đường thẳng a (điểm M nằm ngoài đường thẳng a hoặc đường thẳng a không đi qua điểm M ), kí hiệu là: \mathrm{M} aMa

2. Ba điểm thẳng hàng

- Ba điểm cùng thuộc một đường thẳng ta nói chúng thẳng hàng

- Ba điểm không cùng thuộc bất kỳ đường thẳng nào ta nói chúng không thẳng hàng.

3. Đường thẳng trùng nhau, cắt nhau, song song

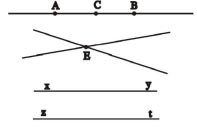
- Hai đường thẳng A B và B C như hình vẽ bên là hai đường thẳng trùng nhau.

- Hai đường thẳng chỉ có một điểm chung ta nói chúng cắt nhau, điểm chung đó được gọi là giao điểm (điểm E là giao điểm)

- Hai đường thẳng không có điểm chung nào ta nói chúng song song với nhau.

 

 

 

 

 

 

 

 

 

.....................

Chia sẻ bởi: 👨 Trịnh Thị Thanh
Liên kết tải về

Chọn file cần tải:

  • Tóm tắt công thức Toán cấp 2 285 KB Tải về
Tìm thêm: Toán THCS Toán 6 Toán lớp 7 Toán 7 Toán 8 Toán 9 Toán lớp 6
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨

Tài liệu tham khảo khác

Chủ đề liên quan

Có thể bạn quan tâm

Xem thêm

Mới nhất trong tuần

Đóng
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ
Chia sẻ
Chia sẻ FacebookChia sẻ Twitter
Đóng