Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn (không bao gồm tài liệu cao cấp) và trải nghiệm website không quảng cáo
Tìm hiểu thêm »Bài 1. Cho A và B là các ma trận đối xứng thực có tất cả các giá trị riêng đều lớn hơn 1. Gọi λ là một giá trị riêng của ma trận AB. Chứng minh rằng |λ| > 1.
Bài 2. Cho f: R → R là hàm khả vi cấp hai. Giả sử f(0)=0. Chứng minh rằng tồn tại ξ thuộc (-π/2, π/2) sao cho f''(ξ) = f(ξ)(12tan2ξ)
Bài 3. Có 2n sinh viên trong một trường học (n thuộc N, n ≥2). Mỗi tuần $n$ sinh viên đi du lịch. Sau một số chuyến du lịch, điều kiện sau được thỏa mãn: mỗi hai sinh viên được đi cùng nhau ít nhất một chuyến. Số chuyến du lịch tối thiểu để điều này xảy ra là bao nhiêu?
Bài 4. Cho n ≥ 3 và x1, x2, ..., xn là các số thực không âm. Ta định nghĩa: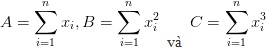
Chứng minh rằng (n1)A2B(n - 2)B2 ≥ A4(2n - 2)AC
Bài 5. Tồn tại hay không dãy (an) các số phức sao cho với mọi số nguyên dương p, ta có ![]() hội tụ nếu và chỉ nếu p không nguyên tố?
hội tụ nếu và chỉ nếu p không nguyên tố?
Bài 1. Cho z là số phức thỏa mãn |z1| ≥ 2. Chứng minh rằng: |z31| > 1
Bài 2. Cho p và q là các số nguyên dương nguyên tố cùng nhau. Chứng minh rằng: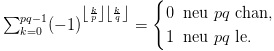
(Trong đó |x| là phần nguyên của x.)
Bài 3. Giải sử v1, v2, ..., vd là các vector đơn vị trong Rd. Chứng minh rằng tồn tại vector đơn vị u sao cho ![]() với i = 1, 2, ..., d.
với i = 1, 2, ..., d.
(Ở đây kí hiệu tích vô hướng thông thường trên Rd).
Bài 4. Tồn tại hay không tập vô hạn M gồm các số nguyên dương sao cho với mọi a, b thuộc M và a < b mà a+b là một số bình phương tự do.
(Một số nguyên dương được gọi là bình phương tự do nếu không có số chính phương lớn hơn 1 là ước của nó. Ví dụ, 10 là bình phương tự do nhưng 18 thì không vì nó có ước là 9 = 32.)
Bài 5. Xét một vòng cổ tròn gồm 2013 hạt. Mỗi hạt được sơn màu trắng hoặc màu xanh. Một cách sơn vòng cổ được gọi là tốt nếu giữa bất kì 21 hạt liên tiếp nào cũng có ít nhất một hạt màu xanh. Chứng minh rằng số cách sơn tốt của vòng cổ này là số lẻ.
(Hai cách sơn khác nhau trên một số hạt, nhưng có thể đạt được bằng cách quay hay lật chuỗi hạt, thì được tính là các cách sơn khác nhau.)
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: