Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn (không bao gồm tài liệu cao cấp) và trải nghiệm website không quảng cáo
Tìm hiểu thêm »
ĐẠI HỌC SƯ PHẠM THÀNH PHỐ
|
KỲ THI OLYMPIC TOÁN SINH VIÊN 2013MÔN: TOÁN HỌC |
Câu 1:
Cho |q| < 1 và limn-→∞ εn = 0
Giả sử dãy (an) không âm và thoả mãn: an1 ≤ qanεn, với mọi n thuộc N
Chứng minh: limn→∞ an = 0
Câu 2: Giả sử hai dãy (an), (bn) thoả các điều kiện sau: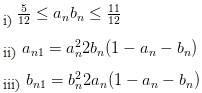
Tìm limn→∞ an; limn→∞ bn
Câu 3:
Cho P(x),Q(x) là các đa thức hệ số thực thoả mãn:
P[exxQ(x)x2Q2(x)] = Q[exxP(x)x2P2(x)], với mọi x thuộc R
Chứng minh P ≡ Q
Câu 4:
Cho f liên tục trên [a;b], khả vi trên (a,b) và f'(x) # 0 với mọi x thuộc (a, b)
Chứng minh rằng: ![]()
Câu 5: Cho a1, a2,...., a2013; b1, b2, ..., b2013 > 0 sao cho: ax1ax2...ax2013 ≥ bx1bx2...bx2013, với mọi x thuộc R
Xét tính đơn điệu của hàm số: ![]()
Câu 6: Cho f thuộc C2[0; a], a > 0, f(x) ≥ 0, f''(x) ≥ 0, với mọi x thuộc [0; a]
Giả sử f(0) = f(a) = 1. Gọi m = min[0; a]f(x), chứng minh: ![]()
Bài 1: Cho A là ma trận cấp 2 × 3 và B là ma trận cấp 3 × 2 thỏa:
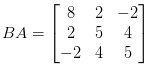
Tìm AB
Bài 2: Cho n là số nguyên dương, x, a, b là các số thực với a # b. Ký hiệu M_n là ma trận vuông cấp 2n thỏa:
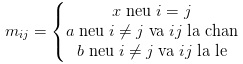
Tìm: ![]()
Bài 3: Cho A thuộc Mn(R). Chứng minh rằng AtA và At có cùng hạng.
Bài 4: Cho ma trận A như sau với bi # 0, với mọi i thuộc {1; 2; ... ; n}

Chứng minh rằng (A) ≥ n - 1
Bài 5:
a) Cho x1, ..., xn là n vector khác không của kgvt V và φ: V → V là một phép biến đổi tuyến tính thỏa φx1 = x2, φxk = xk - xk-1 với k = 2,3,…,n
Chứng minh rằng hệ vector x1,..., xn độc lập tuyến tính.
b) Chứng minh rằng hệ vector {|x - 1|, |x - 2|, ..., |x - n|} độc lập tuyến tính trong không gian các hàm số liên tục trên R
Bài 6:
Cho A,B là hai ma trận đối xứng cấp n. Giả sử tồn tại hai ma trận X,Y cấp n thỏa det(AXBY) # 0. Chứng minh det(A2B2) # 0
Bài 7:
Cho A, B, C, D thuộc Mn(R) thỏa ABt và CDt là hai ma trận đối xứng và ADt - BCt = I. Chứng minh rằng: AtD - CtB = I
Bài 8:
Cho P,Q,U,V là các ma trận cấp 2 thỏa U,V là 2 nghiệm phân biệt của phương trình X2 - PXQ = 0 và U-V khả nghịch.
Chứng minh Tr(UV) = Tr(P) và det(UV) = det(Q)
Bài 9: Cho P là đa thức hệ số thực có n nghiệm thực phân biệt lớn hơn 1. Xét Q(x) = (x21)P(x)P'(x)x(P2(x)P'2(x))
Q(x) có ít nhất 2n-1 nghiệm thực phân biệt đúng hay sai?
Download tài liệu để xem thêm chi tiết.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: