Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn (không bao gồm tài liệu cao cấp) và trải nghiệm website không quảng cáo
Tìm hiểu thêm »Để giúp các bạn học sinh lớp 8 có thêm nhiều tư liệu học tập Download.vn giới thiệu Chuyên đề Hình thoi. Tài liệu tổng quát toàn bộ kiến thức lý thuyết như: định nghĩa, tính chất, dấu hiệu nhận biết và bài tập về hình thoi. Sau đây là nội dung chi tiết mời các bạn cùng tham khảo và tải tài liệu tại đây.
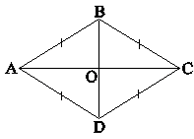
Hình thoi là tứ giác có bốn cạnh bằng nhau, là hình bình hành có 2 cạnh liền kề bằng nhau hoặc có đường chéo vuông góc với nhau.
Hình thoi là một hình bình hành đặc biệt.
Hình thoi là hình có
Vì hình thoi là một dạng đặc biệt của một hình bình hành nên nó sẽ có đầy đủ tính chất của hình bình hành kèm thêm một số tính chất khác như:
Ví dụ 1:
Cho hình thoi ABCD, độ dài mỗi cạnh là 13cm. Gọi O là giao điểm của hai đường chéo. Vẽ OH vuông góc AD. Biết OH = 6cm, tính tỉ số của hai đường chéo BD và AC.
Giải
* Tìm cách giải
Vẽ thêm BK vuông góc với AD để dùng định lí đường trung bình của tam giác, định lí Py-ta-go tính bình phương độ dài của mỗi đường chéo.
* Trình bày lời giải
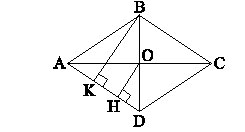
Vẽ BK vuông góc AD.
Xét DBKD có OH // BK (vì cùng vuông góc với AD) và OB = OD nên KH = HD.
Vậy OH là đường trung bình của DBKD.
Suy ra do đó BK = 12cm.
Xét DABK vuông tại K có AK2 = AB2 – BK2 = 132 – 122 = 25 ⇒ AK = 5cm do đó KD = 8cm.
Xét DBKD vuông tại K có BD2 = BK2 + KD2 = 122 + 82 = 208.
Xét DAOH vuông tại H có OA2 = OH2 + AH2 = 62 + 92 = 117.
Ví dụ 2:
Cho tam giác ABC cân tại A, hai đường cao BE và CF cắt nhau tại H. Đường thẳng AH cắt EF tại D, cắt BC tại G. Gọi M và N lần lượt là hình chiếu của G trên AB và AC. Chứng minh rằng tứ giác DNGM là hình thoi.
*Tìm cách giải
Dùng định lí đường trung bình của tam giác ta chứng minh được tứ giác DNGM là hình bình hành. Sau đó chứng minh hai cạnh kề bằng nhau.
*Trình bày lời giải
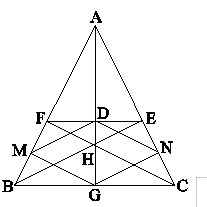
DABE = DACF (cạnh huyền, góc nhọn)
⇒ AE = AF và BE = CF.
Vì H là trực tâm của DABC nên AH là đường cao, đồng thời là đường trung tuyến, từ đó GB = GC và DE = DF.
Vì H là trực tâm của DABC nên AH là đường cao, đồng thời là đường trung tuyến, từ đó GB = GC và DE = DF.
Xét DEBC có GN // BE (cùng vuông góc với AC) và GB = GC nên NE = NC.
Chứng minh tương tự ta được MF = MB.
Dùng định lí đường trung bình của tam giác ta chứng minh được DM // GN và DM = GN nên tứ giác DNGM là hình bình hành.
Mặt khác, DM = DN (cùng bằng ![]() \(\frac{1}{2}\) của hai cạnh bằng nhau) nên DNGM là hình thoi.
\(\frac{1}{2}\) của hai cạnh bằng nhau) nên DNGM là hình thoi.
Bài 1. Một hình thoi có góc nhọn bằng 30o. Khoảng cách từ giao điểm của hai đường chéo đến mỗi cạnh bằng h. Tính độ dài mỗi cạnh của hình thoi.
Bài 2. Cho hình thoi ABCD, chu vi bằng 8cm. Tìm giá trị lớn nhất của tích hai đường chéo.
Bài 3. Cho hình thoi ABCD, góc A là 40 độ. Gọi M là trung điểm của AB. Vẽ DH vuông góc với CM. Tính số đo của góc MHB.
Bài 4. Cho hình thoi ABCD. Trên nửa mặt phẳng bờ BD có chứa điểm C, vẽ hình bình hành BDEF có DE = DC. Chứng minh rằng C là trực tâm của tam giác AEF.
............
Tải file tài liệu để xem thêm nội dung chi tiết
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: