Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn (không bao gồm tài liệu cao cấp) và trải nghiệm website không quảng cáo
Tìm hiểu thêm »Giải Toán 6 trang 65, 66 Cánh diều tập 2 được biên soạn rất chi tiết, hướng dẫn các em phương pháp giải rõ ràng để các em hiểu được bài Tỉ số - Tỉ số phần trăm nhanh nhất. Đồng thời qua giải Toán lớp 6 trang 65, 66 học sinh tự rèn luyện củng cố, bồi dưỡng và kiểm tra vốn kiến thức toán của bản thân mình để học tốt chương 5.
Với lời giải Toán 6 trang 65, 66 chi tiết từng phần, từng bài tập, các em dễ dàng ôn tập, củng cố kiến thức, luyện giải Chương V Toán 6 tập 2 Cánh diều thuật nhuần nhuyễn. Vậy sau đây là nội dung chi tiết tài liệu, mời các bạn cùng theo dõi và tải tại đây nhé.
Viết thương trong phép chia số 1 000 cho số 10 để so sánh chúng.
Gợi ý đáp án
Thương 1 000 : 10 (cũng kí hiệu là ![]() \(\frac{{1000}}{{10}}\) ) thể hiện sự so sánh số 1 000 với số 10.
\(\frac{{1000}}{{10}}\) ) thể hiện sự so sánh số 1 000 với số 10.
Bạn Phương đi bộ với vận tốc 4 km/h. Bạn Quân đi bộ với vận tốc 5 km/h. Tính tỉ số giữa vận tốc của bạn Phương và vận tốc của bạn Quân.
Gợi ý đáp án
Để tính tỉ số giữa vận tốc của bạn Phương và vận tốc của bạn Quân, ta làm như sau:
Vận tốc của bạn Phương là 4 (km/h)
Vận tốc của bạn Quân là 5 (km/h)
=> Tỉ số giữa vận tốc của bạn Phương và vận tốc của bạn Quân là:

Vậy tỉ số giữa vận tốc của bạn Phương và vận tốc của bạn Quân là ![]() \(\frac{4}{5}\)
\(\frac{4}{5}\)
Xe ô tô tải đi với vận tốc 45 km/h, xe ô tô con đi với vận tốc 60 km/h. Vận tốc của xe ô tô tải bằng bao nhiêu phần trăm vận tốc của xe ô tô con?
Gợi ý đáp án
Vận tốc của xe ô tô tải bằng số phần trăm vận tốc của xe ô tô con là:
![]() \(\frac{{45}}{{60}}.100\% = 75\%\)
\(\frac{{45}}{{60}}.100\% = 75\%\)
Vậy vận tốc của xe ô tô tải bằng 75% vận tốc của xe ô tô con.
Tính tỉ số của:
a) ![]() \(\frac{4}{3}\)m và 75cm
\(\frac{4}{3}\)m và 75cm
b) ![]() \(\frac{7}{{10}}\) giờ và 25 phút
\(\frac{7}{{10}}\) giờ và 25 phút
c) 10kg và 10 tạ.
Gợi ý đáp án
a) Đổi 75cm = ![]() \(\frac{{75}}{{100}} = \frac{3}{4} m\)
\(\frac{{75}}{{100}} = \frac{3}{4} m\)
=> Tỉ số: ![]() \(\frac{4}{3}:\frac{3}{4} = \frac{{16}}{9}.\)
\(\frac{4}{3}:\frac{3}{4} = \frac{{16}}{9}.\)
b) Đổi 25 phút = ![]() \(\frac{{25}}{{60}} = \frac{5}{{12}}\) giờ
\(\frac{{25}}{{60}} = \frac{5}{{12}}\) giờ
=> Tỉ số: ![]() \(\frac{7}{{10}}:\frac{5}{{12}} = \frac{{42}}{{25}}\)
\(\frac{7}{{10}}:\frac{5}{{12}} = \frac{{42}}{{25}}\)
c) Đổi 10 tạ = 1000 kg
=> Tỉ số: 10:1000 = ![]() \(\frac{1}{{100}}\)
\(\frac{1}{{100}}\)
Tính tỉ số phần trăm (làm tròn đến hàng phần mười) của:
a) 16 và 75;
b) 6,55 và 8,1.
Gợi ý đáp án
a) Tỉ số phần trăm của 16 và 75 là:
![]() \(\frac{{16}}{{75}}.100\% = 21,3\%\)
\(\frac{{16}}{{75}}.100\% = 21,3\%\)
b) Tỉ số phần trăm của 6,55 và 8,1 là:
![]() \(\frac{6,55}{8,1}.100\%=80,9\%\)
\(\frac{6,55}{8,1}.100\%=80,9\%\)
Một doanh nghiệp thống kê số lượng xi măng bán được trong bốn tháng cuối năm 2019 ở biểu đồ trong Hình 1.
a) Hỏi tháng nào doanh nghiệp bán được nhiều xi măng nhất? Ít xi măng nhất?
b) Tính tỉ số phần trăm của số lượng xi măng bán ra trong tháng 12 và tổng số lượng xi măng bán ra trong cả bốn tháng (làm tròn kết quả đến hàng đơn vị).
Gợi ý đáp án
Theo biểu đồ, ta có:
Khối lượng xi măng bán ra trong tháng 9 là: 3.30 = 90 (tấn).
Khối lượng xi măng bán ra trong tháng 10 là: 3.30 = 90 (tấn).
Khối lượng xi măng bán ra trong tháng 11 là: 4.30 = 120 (tấn).
Khối lượng xi măng bán ra trong tháng 12 là: 4.30 + 15 = 135 (tấn).
a) Tháng doanh nghiệp bán được nhiều xi măng nhất là tháng 12 với 135 tấn.
Tháng 9 và tháng 10 doanh nghiệp bán ra được ít xi măng nhất với 90 tấn.
b) Tổng số lượng xi măng bán ra trong cả bốn tháng là: 90 + 90 + 120 + 135 = 435 tấn.
Tỉ số phần trăm của số lượng xi măng bán ra trong tháng 12 và tổng số lượng xi măng bán ra trong cả bốn tháng là: ![]() \(\frac{135}{435}.100\%\ =\ 31.03\%\)
\(\frac{135}{435}.100\%\ =\ 31.03\%\)
Vậy tỉ số phần trăm của số lượng xi măng bán ra trong tháng 12 và tổng số lượng xi măng bán ra trong cả bốn tháng là 31,03%.
Xếp loại thi đua ba tổ lao động của một đội sản xuất được thống kê như sau (đơn vị: người):
| Xếp loại thi đua Tổ |
Giỏi | Khá | Đạt |
| Tổ 1 | 17 | 8 | 5 |
| Tổ 2 | 13 | 8 | 4 |
| Tổ 3 | 13 | 7 | 5 |
a) Mỗi tổ lao động có bao nhiêu người?
b) Đội trưởng thông báo rằng tỉ số phần trăm của số lao động giỏi ở cả đội so với số người ở cả đội là lớn hơn 53%. Thông báo đó của đội trưởng có đúng không?
Gợi ý đáp án
a) Số người của tổ 1 là: 17 + 8 + 5 = 30 (người).
Số người của tổ 2 là: 13 + 8 + 4 = 25 (người).
Số người của tổ 3 là: 13 + 7 + 5 = 25 (người).
Vậy số người của tổ 1, tổ 2 và tổ 3 lần lượt là: 30 người, 25 người, 25 người.
b) Tổng số người của cả đội là: 30 + 25 + 25 = 80 (người).
Số lao động giỏi của cả đội là: 17 + 13 + 13 = 43 (người).
Tỉ số phần trăm của số lao động giỏi của cả đội so với số người cả đội là:
![]() \(\frac{43}{80}.100\%\ =\ 53,75\%\) > 53%
\(\frac{43}{80}.100\%\ =\ 53,75\%\) > 53%
Vậy thông báo của đội trưởng hoàn toàn chính xác.
Xếp loại thi đua ba tổ lao động của một đội sản xuất được thống kê như sau:
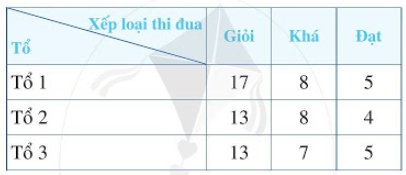
a) Mỗi tổ lao động có bao nhiêu người?
b) Đội trưởng thông báo rằng tỉ số phần trăm của số lao động giỏi ở cả đội so với số người ở cả đội là lớn hơn 53%. Thông báo đó của đội trưởng có đúng không?
Gợi ý đáp án
a) Tổ 1 có 17+8+5=30 người
Tổ 2 có 13+8+4=25 người
Tổ 3 có 13+7+5=25 người.
b) Số lao động giỏi ở cả đội là: 17+13+23=43 người
Số người ở cả đội là: 30+25+25=80 người.
Tỉ số phần trăm của số lao động giỏi ở cả đội so với số người ở cả đội là:
![]() \(\frac{43}{80} \cdot 100 \%=53,75 \%\)
\(\frac{43}{80} \cdot 100 \%=53,75 \%\)
=> Đội trưởng thông báo rằng tỉ số phần trăm của số lao động giỏi ở cá đội so với số người ở cả đội là lớn hơn 53 \% là đúng.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: