Cách chứng minh tứ giác nội tiếp đường tròn Chứng minh tứ giác nội tiếp đường tròn

Cách chứng minh tứ giác nội tiếp đường tròn tổng hợp 6 cách chứng minh ví dụ minh họa kèm theo 6 bài tập có lời giải chi tiết.

Cách chứng minh tứ giác nội tiếp đường tròn là một trong những bài toán cơ bản trong chương trình lớp 9 hiện hành. Qua tài liệu này giúp các bạn học sinh tham khảo, hệ thống lại kiến thức để giải nhanh các bài tập hình học về tứ giác nội tiếp. Ngoài ra để nâng cao kiến thức môn Toán thật tốt các bạn xem thêm một số tài liệu như: cách tính bán kính đường tròn ngoại tiếp tam giác, tâm đường tròn ngoại tiếp tam giác.

I. Cách chứng minh tứ giác nội tiếp đường tròn

1) Chứng minh cho bốn đỉnh của tứ giác cách đều một điểm nào đó

Ví dụ: Cho một điểm O cố định và tứ giác ABCD.

Nếu học sinh chứng minh được bốn điểm A, B, C, D cách đều điểm O với khoảng cách bằng R, tức OA = OB = OC = OD = R thì điểm O chính là tâm đường tròn đi qua bốn điểm A, B, C, D. Hay nói cách khác, tứ giác ABCD nội tiếp đường tròn tâm O bán kính R.

2) Chứng minh tứ giác có tổng 2 góc đối bằng 180°

Cho tứ giác ABCD

Tứ giác ABCD là tứ giác nội tiếp nếu góc A + góc C = 180° hoặc góc B + góc D = 180°

Phương pháp này được xuất phát từ chính định nghĩa của tứ giác nội tiếp. Nội dung của phương pháp này như sau: “Nếu tứ giác ABCD có tổng hai góc đối bằng 180 độ thì tứ giác đó nội tiếp”

Hệ quả của nội dung này là:

Cho tứ giác ABCD:

+ Nếu BAD = BCD = 90 độ thì tứ giác ABCD nội tiếp đường tròn tâm O đường kính BD

+ Nếu tổng hai góc kề bù EAD = BCD thì tứ giác ABCD nội tiếp

3) Chứng minh từ hai đỉnh cùng kề một cạnh cùng nhìn một cạnh dưới hai góc bằng nhau

Cho tứ giác ABCD

Tứ giác ABCD là tứ giác nội tiếp ⇔ góc DAC = góc DBC cùng chắn cung DC

Phương pháp này áp dụng khi đề bài cho tứ giác ABCD và những dữ kiện gợi ý tính được rằng DAC = DBC = 90 độ. Từ đó, học sinh có thể kết luận tứ giác ABCD nội tiếp đường tròn.

4) Nếu một tứ giác có tổng số đo hai góc đối bằng thì tứ giác đó nội tiếp được trong một đường tròn

Cho tứ giác ABCD

Tứ giác ABCD là tứ giác nội tiếp ⇔ góc A + góc C = góc B + góc D. Đây là trường hợp đặc biệt của cách thứ 2.

5) Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối của đỉnh đó thì nội tiếp được trong một đường tròn

Cho tứ giác ABCD

Tứ giác ABCD là tứ giác nội tiếp nếu góc ngoài đỉnh A bằng góc C, hoặc góc ngoài đỉnh B bằng góc D.

Ở phương pháp này, học sinh chú ý phải nhìn đúng hình đúng góc, nếu không sẽ bị tình trạng chứng minh sai nhưng kết quả đúng và ảnh hưởng tới những câu tiếp theo. Cụ thể, khi đề bài cho tứ giác ABCD và chứng minh được góc ngoài tại đỉnh A bằng góc C của tứ giác (góc A và góc C đối đỉnh) thì có thể kết luận tứ giác ABCD là tứ giác nội tiếp.

6) Chứng minh bằng phương pháp phản chứng

Với cách này, các em chứng minh tứ giác là các hình đặc biệt như hình vuông, hình chữ nhật, hình thoi, hình bình hành.

II. Ví dụ chứng minh tứ giác nội tiếp đường tròn

Ví dụ: Cho đường tròn tâm O. Từ điểm A ở bên ngoài đường tròn (O) vẽ hai tiếp tuyến AB và AC với đường tròn (B, C là hai tiếp điểm). Trên BC lấy điểm M, vẽ đường thẳng vuông góc với OM tại M, cắt AB và AC lần lượt tại E và D. Chứng minh các tứ giác EBMO và DCOM nội tiếp được trong đường tròn. Xác định tâm các đường tròn đó.

Giải

– Chứng minh tứ giác EBMO nội tiếp:

+ Có OM ⊥ ME (gt) nên góc OME bằng 90^o

+ OB ⊥ BE (BE là tiếp tuyến của (O)) nên góc OBE bằng 90^o

Vậy, tứ giác EBMO có hai góc vuông cùng nhìn cạnh OE nên tứ giác EBMO nội tiếp trong đường tròn đường kính OE.

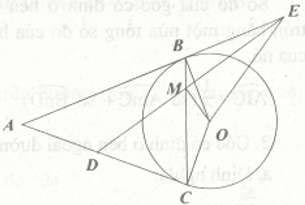
– Chứng minh tứ giác DCOM nội tiếp

+ Có OM ⊥ OD (gt) nên góc OMD bằng 90^o

+ CD ⊥ OC (CĐ là tiếp tuyến của (O)) nên góc OCD bằng 90^o

Vậy, tứ giác DCOM có hai góc vuông cùng nhìn cạnh OD nên tứ giác DCOM nội tiếp trong đường tròn đường kính OD.

III. Bài tập chứng minh tứ giác nội tiếp đường tròn

Bài 1: Cho bốn điểm A, B, C, D theo thứ tự đó nằm trên đường tròn tâm O; I là điểm chính giữa của cung AB (không chứa C và D); I là điểm chính giữa cung AB (không chứa C và D). IC và AD kéo dài giao nhau tại E; ID kéo dài cắt BC kéo dài tại F. Hãy chứng minh rằng tứ giác CDEF nội tiếp đường tròn.

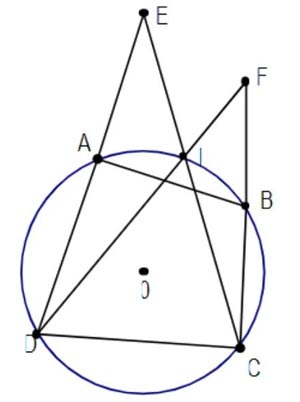
Hướng dẫn giải:

Để chứng minh được rằng tứ giác CDEF nội tiếp, ta có thể chứng minh 2 đỉnh không thuộc cạnh đó cùng nhìn cạnh đã chọn dưới 2 góc bằng nhau.

Chẳng hạn ta chọn cạnh DC, hãy tìm ra hai đỉnh E và F cùng nhìn DC dưới hai góc bằng nhau. Trong bài toán này ta chọn cạnh EF và chứng minh góc EDF bằng góc ECF bằng nửa số đo cung AI bằng nửa số đo cung BI.

Bài 2: Cho hình vuông ABCD, dựng góc xAy bằng 45 độ sao cho tia Ax cắt BD tại P, cắt BC tại Q; Tia Ay cắt BD tại F, CD tại E.

Chứng minh rằng:

a. Tứ giác ABQF nội tiếp

b. Tứ giác APED nội tiếp

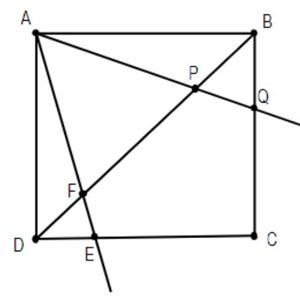
Hướng dẫn giải:

a. Hãy chỉ ra hai đỉnh A và B cùng nhìn đoạn QF dưới hai góc bằng 45 độ.

b. Hãy chỉ ra hai đỉnh A và D cùng nhìn đoạn EP dưới hai góc bằng 45 độ.

Bài 3: Cho đường tròn tâm O, M là một điểm nằm bên ngoài đường tròn. Từ M tạo hai tiếp tuyến MA và MB với đường tròn (A, B là hai tiếp điểm). Qua M vẽ cát tuyến MCD. Gọi I là trung điểm của CD.

a. Chứng minh tứ giác AIOB nội tiếp trong một đường tròn.

b. Gọi K là trung điểm của AM. Tia BK cắt đường tròn tại điểm thứ hai là P. Tia MP cắt đường tròn tại điểm thứ 2 là N. Chứng minh rằng AK²=KP.KB

c. Chứng minh rằng AM // BN

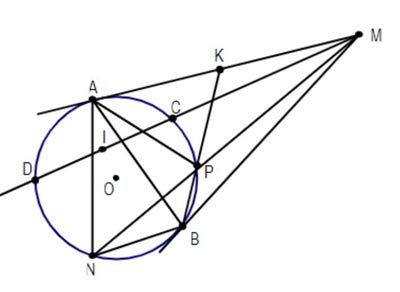
Hướng dẫn giải:

a. Chứng minh 5 đỉnh M, A, I, O, B cùng nhìn đoạn OM dưới một góc vuông. Từ đó suy ra tứ giác AIOB nội tiếp.

b. Chứng minh hai tam giác đồng dạng: tam giác AKB và tam giác PKA.

c. Chứng minh hai góc MNB và KMN bằng nhau. Tam giác AKB và tam giác PKA đồng dạng, suy ra hai tam giác BKM và MKP đồng dạng.

Bài 4: Cho tam giác ABC nhọn, đường cao BM và CN cắt nhau tại H. Chứng minh các tứ giác AMHN và BNMC là hai tứ giác nội tiếp đường tròn.

Bài 5: Cho đường tròn tâm O đường kính AB, gọi I là trung điểm của OA, dây CD vuông góc với AB tại I. Lấy K tùy ý trên cung BC nhỏ, AK cắt CD tại H.

a. Chứng minh BIHK là tứ giác nội tiếp đường tròn

b. Không phụ thuộc vào vị trí điểm K, hãy chứng minh AH.AK có giá trị

c. Kẻ DN và AC lần lượt vuông góc cạnh CB và DM. Chứng minh MN, AB, CD là các đường thẳng đồng quy.

Bài 6 Cho tam giác ABC nhọn với AB < AC có AD là đường phân giác. Đường thẳng qua C song song với AD cắt đường trung trực của AC tại E. Đường thẳng qua B song song với AD cắt đường trung trực của AB tại F.

a. Chứng minh tam giác ABF đồng dạng với tam giác ACE.

b. Chứng minh rằng BE, CF, AD là các đường thẳng đồng quy, gọi điểm đó là G.

c. Từ G kẻ đường thẳng song song với AE cắt đường thẳng BF tại Q. Đường thẳng QE cắt đường tròn ngoại tiếp tam giác GEC tại P. Hãy chứng minh A, P, G, F, Q là các điểm cùng nằm trên một đường tròn.