Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn (không bao gồm tài liệu cao cấp) và trải nghiệm website không quảng cáo
Tìm hiểu thêm »
SỞ GIÁO DỤC VÀ ĐÀO TẠO
|
KỲTHI CHỌN HỌC SINH GIỎI LỚP 9 THCS
|
MÔN THI: TOÁN
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
--------------------------------------------------------------------------------
Câu I. (5,0 điểm).
1) Cho phương trình: x2 - 2mx + 2m - 1 = 0. Chứng minh phương trình luôn có hai nghiệm x1, x2 với mọi m. Tìm giá trị lớn nhất của biểu thức ![]() khi m thay đổi.
khi m thay đổi.
2) (a). Cho ba số hữu tỉ a, b, c thoả mãn ![]() . Chứng minh rằng
. Chứng minh rằng ![]() là số hữu tỉ.
là số hữu tỉ.
(b). Cho ba số hữu tỉ x, y, z đôi một phân biệt. Chứng minh rằng: 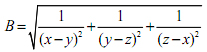 là số hữu tỉ.
là số hữu tỉ.
Câu II. (5,0 điểm).
1) Giải phương trình: ![]()
2) Giải hệ phương trình: 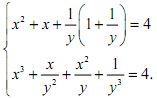
Câu III. (2,0 điểm).
Cho tam giác đều ABC, các điểm D, E lần lượt thuộc các cạnh AC, AB, sao cho BD, CE cắt nhau tại P và diện tích tứ giác ADPE bằng diện tích tam giác BPC.
Tính góc BPE?
Câu IV. (4,0 điểm).
Cho đường tròn tâm O và dây cung AB cố định (O ∉ AB). P là điểm di động trên đoạn thẳng AB (P ≠ A, B và P khác trung điểm AB). Đường tròn tâm C đi qua điểm P tiếp xúc với đường tròn (O) tại A. Đường tròn tâm D đi qua điểm P tiếp xúc với đường tròn (O) tại B. Hai đường tròn (C) và (D) cắt nhau tại N (N ≠ P).
1) Chứng minh rằng góc ANP = góc BNP và bốn điểm O, D, C, N cùng nằm trên một đường tròn.
2) Chứng minh rằng đường trung trực của đoạn ON luôn đi qua điểm cố định khi P di động.
Câu V. (4,0 điểm).
1) Cho a1, a2,..., a45 là số tự nhiên dương thoả mãn a1 < a2 <...< a45 ≤ 130. Đặt dj = aj+1 - aj, (j = 1, 2, ..., 44). Chứng minh rằng ít nhất một trong 44 hiệu dj xuất hiện ít nhất 10 lần.
2) Cho ba số dương a, b, c thoả mãn: ![]()
Chứng minh rằng: ![]()
Download tài liệu để xem thêm chi tiết
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: