Tia phân giác: Lý thuyết & các dạng bài tập Ôn tập Hình học lớp 6

Tải về Bình luận

Tia phân giác giúp các em nắm vững kiến thức lý thuyết, cũng như các dạng bài tập về tia phân giác của góc. Qua đó sẽ hệ thống lại những kiến thức trọng tâm, hiểu kỹ hơn về các dạng bài tập để học tốt môn Toán lớp 6.

Ngoài ra, các em có thể tham khảo thêm cách giải các dạng bài tập Tia phân giác của góc trong sách giáo khoa Toán lớp 6 phần Hình học. Vậy mời các em cùng theo dõi bài viết dưới đây của Download.vn:

Tổng hợp kiến thức tia phân giác của góc

Định nghĩa tia phân giác
Cách vẽ tia phân giác của một góc
Các dạng bài tập tia phân giác của một góc

Định nghĩa tia phân giác

Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.

Tia phân giác của góc

Nếu tia Oz là tia phân giác của góc xOy thì $\widehat{xOz}=\widehat{yOz}=\dfrac{\widehat{xOy}}2$ $\hat{x O z} = \hat{y O z} = \frac{\hat{x O y}}{2}$

Cách vẽ tia phân giác của một góc

Cách 1: Dùng thức đo góc

Cách 2: Gấp giấy

Chú ý: Đường thẳng chứa tia phân giác của một góc là đường phân giác của góc đó.

Các dạng bài tập tia phân giác của một góc

Dạng 1: Nhận biết một tia là tia phân giác của một góc

Phương pháp giải

Vận dụng định nghĩa tia phân giác của một góc. Để chứng tỏ tia Oz la tia phân giác của góc xOy phải có đủ hai điều kiện:

Tia Oz nằm giữa hai tia Ox và Oy (hoặc $\widehat{xOz}+\widehat{yOz}= \widehat{xOy}$ $\hat{x O z} + \hat{y O z} = \hat{x O y}$ ).
$\widehat{xOz}=\widehat{yOz}$ $\hat{x O z} = \hat{y O z}$

Ví dụ 1. (Bài 30 tr. 87 SGK)

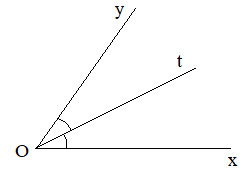
Trên cùng một nửa mặt phẳng chứa bờ Ox, vẽ tia Ot sao cho góc $\widehat{xOt}=25^0,\widehat{xOy}=50^0$ $\hat{x O t} = 25^{0}, \hat{x O y} = 50^{0}$

a) Tia Ot có nằm giữa hai tia Ox và Oy không?

b) So sánh góc tOy và góc xOt.

c ) Tia Ot có là tia phân giác của góc xOy không? Vì sao?

Gợi ý đáp án:

Bài 30

a) Trên cùng một nửa mặt phẳng bờ chứa tia Ox có $\widehat{xOt}<\widehat{xOy}$ $\hat{x O t} < \hat{x O y}$ (vì $25^{0} < 50^{0}$ ) nên tia Ot nằm giữa hai tia Ox và Oy (1)

b) Vì tia Ot nằm giữa hai tia Ox,Oy nên:

$\widehat{xOt}+\widehat{yOt}= \widehat{xOy}$ $\hat{x O t} + \hat{y O t} = \hat{x O y}$

Thay số ta được: $25^0+ \widehat{tOy}=50^0$ $25^{0} + \hat{t O y} = 50^{0}$

Suy ra $\widehat{tOy}=50^0-25^0=25^0$ $\hat{t O y} = 50^{0} - 25^{0} = 25^{0}$

Vậy $\widehat{xOt}=\widehat{tOy}\,(=25^0)$ $\hat{x O t} = \hat{t O y} (= 25^{0})$ (2)

c) Từ (1) và (2) ta có: Tia Ot nằm giữa hai tia Ox và Oy và $\widehat{xOt}=\widehat{tOy}$ $\hat{x O t} = \hat{t O y}$ nên Ot là tia phân giác của góc xOy.

Ví dụ 2. Cho hai góc tù, vừa bằng nhau vừa kề nhau là $\widehat{AOM}$ $\hat{A O M}$ và $\widehat{BOM}$ $\hat{B O M}$ . Gọi ON là tia đối của tia OM. Tia ON có phải là tia phân giác của góc AOB không? Vì sao?

Gợi ý đáp án:

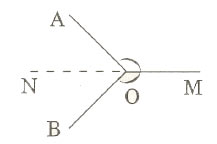
Ví dụ 2

Hai góc kề AOM và BOM có $\widehat{AOM} +\widehat{BOM}>180^{0}$ $\hat{A O M} + \hat{B O M} > 180^{0}$ nên tia ON nằm giữa hai tia OA, OB (1)

Ta có $\widehat{NOA} = \widehat{NOBM}$ $\hat{N O A} = \hat{N O B M}$ (Cùng bù với hai góc bằng nhau). (2)

Từ (1) và (2) suy ra tia ON là tia phân giác của góc AOB.

Dạng 2: Tính số đo góc

Phương pháp giải

Dựa và nhận xét: Số đo của góc tạo bởi tia phân giác với mỗi cạnh của góc bằng nửa số đo của góc đó.

Ví dụ 1: Cho góc AOB có số đo là 140 độ. Vẽ tia OC bất kì nằm trong góc đó. Gọi OM và ON theo thứ tự là các tia phân giác của các góc AOC và BOC. Tính $\widehat{MON}$ $\hat{M O N}$ .

Gợi ý đáp án:

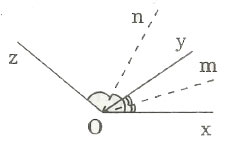
Ví dụ 1

Tia OM là tia phân giác của góc AOC nên tia OM nằm giữa hai tia OA, OC và $\widehat{MOC} =\frac{1}{2} \widehat{AOC}$ $\hat{M O C} = \frac{1}{2} \hat{A O C}$ . Tia ON là tia phân giác của góc BOC nên tia ON nằm giữa hai tia OB, OC và $\widehat{NOC} =\frac{1}{2} \widehat{BOC}$ $\hat{N O C} = \frac{1}{2} \hat{B O C}$ .

Mặt khác tia OC nằm giữa hai tia OA, OB (đề bài) nên tia OC nằm giữa hai tia OM, ON.

Suy ra $\widehat{MON}=\widehat{MOC} + \widehat{NOC}= \frac{\widehat{AOC}+\widehat{BOC}}{2} + \frac{\widehat{AOB}}{2} = 70.$ $\hat{M O N} = \hat{M O C} + \hat{N O C} = \frac{\hat{A O C} + \hat{B O C}}{2} + \frac{\hat{A O B}}{2} = 70.$

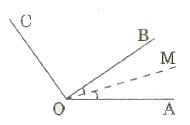
Ví dụ 2: Trên nửa mặt phẳng bờ chứa tia OA vẽ các tia OB, OC sao cho $\widehat{AOB}<\widehat{AOC}$ $\hat{A O B} < \hat{A O C}$ .

Vẽ tia phân giác OM của góc AOB.

a) Trong ba tia OB, OC, OM tia nào nằm giữa hai tia còn lại?

b) Chứng tỏ rằng $\widehat{MOC}=\frac{\widehat{AOC}+\widehat{BOC}}{2}$ $\hat{M O C} = \frac{\hat{A O C} + \hat{B O C}}{2}$ .

Gợi ý đáp án:

Tia OM là tia phân giác của góc AOB nên $\widehat{AOM}=\widehat{BOM}=\frac{\widehat{AOB}}{2}$ $\hat{A O M} = \hat{B O M} = \frac{\hat{A O B}}{2}$ .

Trên nửa mặt phẳng bờ chứa tia OA có $\widehat{AOM}<\widehat{AOB}<\widehat{AOC}$ $\hat{A O M} < \hat{A O B} < \hat{A O C}$ nên tia OB nằm giữa hai tia OM và OC (1)

đồng thời tia OM nằm giữa hai tia OA, OC (2)

Từ (1) suy ra $\widehat{MOC}=\widehat{MOB}+\widehat{BOC}$ $\hat{M O C} = \hat{M O B} + \hat{B O C}$

Từ (2) suy ra $\widehat{MOC}=\widehat{AOC}-\widehat{AOM}$ $\hat{M O C} = \hat{A O C} - \hat{A O M}$

Vây: $\widehat{MOC}+ \widehat{MOC}=\widehat{MOB}+\widehat{EOC}+\widehat{AOC} -\widehat{AOM}$ $\hat{M O C} + \hat{M O C} = \hat{M O B} + \hat{E O C} + \hat{A O C} - \hat{A O M}$

Ví dụ 2

Hay: $2\widehat{MOC}=\widehat{AOC}+\widehat{BOC} => \widehat{MOC} = \frac{\widehat{AOC}+\widehat{BOC}}{2}$ $2 \hat{M O C} = \hat{A O C} + \hat{B O C} => \hat{M O C} = \frac{\hat{A O C} + \hat{B O C}}{2}$

Dạng 3: Tìm tia phân giác của một góc

Phương pháp giải

Xét từng tia, chọn tia nào thỏa mãn định nghĩa tia phân giác của một góc.

Ví dụ: Tìm trên hình 55 những tia là tia phân rằng O1 = O2 = O3 = O4 .

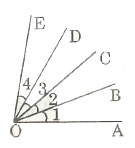
Tìm tia phân giác của một góc

Gợi ý đáp án:

OB là tia phân giác của góc AOC.

OC là tia phân giác của góc BOD và AOE.

OD là tia phân giác của góc COE.

Chia sẻ bởi:

Lê Thị tuyết Mai

Tải về

Liên kết tải về

Tia phân giác: Lý thuyết & các dạng bài tập 166,4 KB Tải về

Tìm thêm: Toán lớp 6

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!