Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn (không bao gồm tài liệu cao cấp) và trải nghiệm website không quảng cáo
Tìm hiểu thêm »Hướng dẫn xây dựng ma trận đề kiểm tra môn Toán THCS giúp thầy cô tham khảo để biết cách xây dựng ma trận, bảng đặc tả đề kiểm tra định kỳ môn Toán theo đúng quy định mới nhất.
Tài liệu chia ra 2 phần, phần 1 là những vấn đề chung về kiểm tra đánh giá, còn phần 2 hướng dẫn xây dựng ma trận, bảng đặc tả môn Toán học kì 1, giữa học kì 1, giữa học kì 2, học kì 2 cho lớp 6, 7, 8 và 9. Ngoài ra, có thể tham khảo hướng dẫn môn Ngữ văn, Lịch sử - Địa lí THCS. Mời thầy cô cùng theo dõi nội dung chi tiết trong bài viết dưới đây:
1. Ma trận đề kiểm tra
a. Khái niệm ma trận đề kiểm tra
b. Cấu trúc một bảng ma trận đề kiểm tra
Cấu trúc 1 bảng ma trận đề kiểm tra gồm các thông tin như sau:
Tên Bảng ma trận - Ký hiệu (nếu cần)
- Cấu trúc từng phần (Prompt Attributes)
+ Cấu trúc và tỷ trọng từng phần
+ Các câu hỏi trong đề kiểm tra (items)
- Các thông tin hỗ trợ khác
c. Thông tin cơ bản của ma trận đề kiểm tra:
d. Ví dụ minh họa mẫu ma trận đề kiểm tra
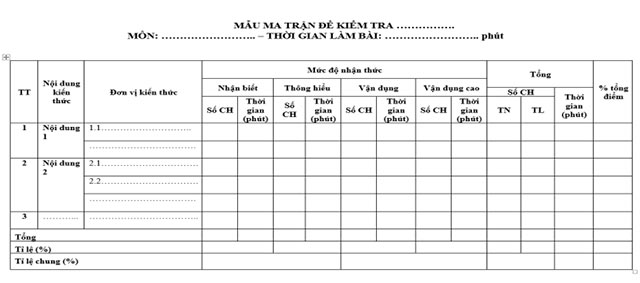
2. Bản đặc tả đề kiểm tra
a. Khái niệm bản đặc tả
Bản đặc tả đề kiểm tra (trong tiếng Anh gọi là test specification hay test blueprint) là một bản mô tả chi tiết, có vai trò như một hướng dẫn để viết một đề kiểm tra hoàn chỉnh. Bản đặc tả đề kiểm tra cung cấp thông tin về cấu trúc đề kiểm tra, hình thức câu hỏi, số lượng câu hỏi ở mỗi loại, và phân bố câu hỏi trên mỗi mục tiêu đánh giá.
Bản đặc tả đề kiểm tra giúp nâng cao độ giá trị của hoạt động đánh giá, giúp xây dựng đề kiểm tra đánh giá đúng những mục tiêu dạy học dự định được đánh giá. Nó cũng giúp đảm bảo sự đồng nhất giữa các đề kiểm tra dùng để phục vụ cùng một mục đích đánh giá. Bên cạnh lợi ích đối với hoạt động kiểm tra đánh giá, bản đặc tả đề kiểm tra có tác dụng giúp cho hoạt động học tập trở nên rõ ràng, có mục đích, có tổ chức và có thể kiểm soát được. Người học có thể sử dụng để chủ động đánh giá việc học và tự chấm điểm sản phẩm học tập của mình. Còn người dạy có thể áp dụng để triển khai hướng dẫn các nhiệm vụ, kiểm tra và đánh giá. Bên cạnh đó, nó cũng giúp các nhà quản lý giáo dục kiểm soát chất lượng giáo dục của đơn vị mình.
b. Cấu trúc bản đặc tả đề kiểm tra
Một bản đặc tả đề kiểm tra cần chỉ rõ mục đích của bài kiểm tra, những mục tiêu dạy học mà bài kiểm tra sẽ đánh giá, ma trận phân bố câu hỏi theo nội dung dạy học và mục tiêu dạy học, cụ thể như sau:
(i) Mục đích của đề kiểm tra
Phần này cần trình bày rõ đề kiểm tra sẽ được sử dụng phục vụ mục đích gì. Các mục đích sử dụng của đề kiểm tra có thể bao gồm (1 hoặc nhiều hơn 1 mục đích):
(ii) Hệ mục tiêu dạy học/ tiêu chí đánh giá
(iii) Bảng đặc tả đề kiểm tra
(iv). Cấu trúc đề kiểm tra
.....
1. Hướng dẫn xây dựng ma trận đề kiểm tra
KHUNG MA TRẬN ĐỀ KIỂM TRA ĐỊNH KÌ MÔN TOÁN – LỚP …
|
TT (1) |
Chương/Chủ đề (2) |
Nội dung/đơn vị kiến thức (3) |
Mức độ đánh giá |
Tổng % điểm (12)
|
|||||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
||||||||
|
TNKQ |
TL |
TNKQ |
TL |
TNKQ |
TL |
TNKQ |
TL |
||||
|
1 |
Chủ đề A |
Nội dung 1 … |
|
|
|
|
|
|
|
|
|
|
Nội dung 2 … |
|
|
|
|
|
|
|
|
|
||
|
Nội dung 3… |
|
|
|
|
|
|
|
|
|
||
|
2
|
Chủ đề B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
...
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
Tổng |
|
|
|
|
|
|
|
|
|
||
|
Tỉ lệ % |
30-40% |
30-40% |
20-30% |
10% |
100 |
||||||
|
Tỉ lệ chung |
70% |
30% |
100 |
||||||||
Ghi chú:
- Cột 2 và cột 3 ghi tên chủ đề như trong Chương trình giáo dục phổ thông môn Toán 2018, gồm các chủ đề đã dạy theo kế hoạch giáo dục tính đến thời điểm kiểm tra.
- Cột 12 ghi tổng % số điểm của mỗi chủ đề.
- Đề kiểm tra cuối học kì dành khoảng 10% -30% số điểm để kiểm tra, đánh giá phần nội dung thuộc nửa đầu của học kì đó.
- Tỉ lệ % số điểm của các chủ đề nên tương ứng với tỉ lệ thời lượng dạy học của các chủ đề đó.
- Tỉ lệ các mức độ đánh giá: Nhận biết khoảng từ 30-40%; Thông hiểu khoảng từ 30-40%; Vận dụng khoảng từ 20-30%; Vận dụng cao khoảng 10%.
- Tỉ lệ điểm TNKQ khoảng 30%, TL khoảng 70%.
- Số câu hỏi TNKQ khoảng 12-15 câu, mỗi câu khoảng 0,2 - 0,25 điểm; TL khoảng 7-9 câu, mỗi câu khoảng 0,5 -1,0 điểm.
2. Hướng dẫn xây dựng bản đặc tả đề kiểm tra
BẢN ĐẶC TẢ MỨC ĐỘ ĐÁNH GIÁ MÔN TOÁN -LỚP ....
| TT | Chương/Chủ đề | Nội dung/Đơn vị kiến thức | Mức độ đánh giá | Số câu hỏi theo mức độ nhận thức | |||
| Nhận biêt | Thông hiểu | Vận dụng | Vận dụng cao | ||||
|
1 |
Chủ đề A |
Nội dung 1. |
Nhận biết - - |
|
|
|
|
|
Thông hiểu - - … |
|
|
|
|
|||
|
Nội dung 2. |
Thông hiểu |
|
|
|
|
||
|
Vận dụng |
|
|
|
|
|||
|
2 |
Chủ đề B |
|
Thông hiểu |
|
|
|
|
|
Vận dụng |
|
|
|
|
|||
|
Vận dụng cao |
|
|
|
|
|||
|
--- |
|
|
Nhận biết |
|
|
|
|
|
Thông hiểu |
|
|
|
|
|||
|
Vận dụng |
|
|
|
|
|||
|
Vận dụng cao |
|
|
|
|
|||
|
Tổng |
|
|
|
|
|
||
|
Tỉ lệ % |
|
|
|
|
|
||
|
Tỉ lệ chung |
|
|
|
||||
Lưu ý:
- Với câu hỏi mức độ nhận biết và thông hiểu thì mỗi câu hỏi cần được ra ở một chỉ báo của mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá tương ứng (1 gạch đầu dòng thuộc mức độ đó).
- Các câu hỏi ở mức độ vận dụng và vận dụng cao có thể ra vào một trong các đơn vị kiến thức.
3. Giới thiệu bản đặc tả của cấp học
BẢNG MÔ TẢ MỨC ĐỘ ĐÁNH GIÁ MÔN TOÁN - LỚP 6
|
TT |
Chủ đề |
Mức độ đánh giá |
|
|
SỐ VÀ ĐẠI SỐ |
|||
|
1 |
Số tự nhiên |
Số tự nhiên và tập hợp các số tự nhiên. Thứ tự trong tập hợp các số tự nhiên
|
Nhận biết: – Nhận biết được tập hợp các số tự nhiên. |
|
Thông hiểu: – Biểu diễn được số tự nhiên trong hệ thập phân. – Biểu diễn được các số tự nhiên từ 1 đến 30 bằng cách sử dụng các chữ số La Mã. |
|||
|
Vận dụng: – Sử dụng được thuật ngữ tập hợp, phần tử thuộc (không thuộc) một tập hợp; sử dụng được cách cho tập hợp. |
|||
|
Các phép tính với số tự nhiên. Phép tính luỹ thừa với số mũ tự nhiên |
Nhận biết: – Nhận biết được thứ tự thực hiện các phép tính. |
||
|
Vận dụng: – Thực hiện được các phép tính: cộng, trừ, nhân, chia trong tập hợp số tự nhiên. – Vận dụng được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng trong tính toán. – Thực hiện được phép tính luỹ thừa với số mũ tự nhiên; thực hiện được các phép nhân và phép chia hai luỹ thừa cùng cơ số với số mũ tự nhiên. – Vận dụng được các tính chất của phép tính (kể cả phép tính luỹ thừa với số mũ tự nhiên) để tính nhẩm, tính nhanh một cách hợp lí. – Giải quyết được những vấn đề thực tiễn (đơn giản, quen thuộc) gắn với thực hiện các phép tính (ví dụ: tính tiền mua sắm, tính lượng hàng mua được từ số tiền đã có, ...). |
|||
|
Vận dụng cao: – Giải quyết được những vấn đề thực tiễn (phức hợp, không quen thuộc) gắn với thực hiện các phép tính. |
|||
|
Tính chia hết trong tập hợp các số tự nhiên. Số nguyên tố. Ước chung và bội chung |
Nhận biết : – Nhận biết được quan hệ chia hết, khái niệm ước và bội. – Nhận biết được khái niệm số nguyên tố, hợp số. – Nhận biết được phép chia có dư, định lí về phép chia có dư. – Nhận biết được phân số tối giản. |
||
|
Vận dụng: – Vận dụng được dấu hiệu chia hết cho 2, 5, 9, 3 để xác định một số đã cho có chia hết cho 2, 5, 9, 3 hay không. – Thực hiện được việc phân tích một số tự nhiên lớn hơn 1 thành tích của các thừa số nguyên tố trong những trường hợp đơn giản. – Xác định được ước chung, ước chung lớn nhất; xác định được bội chung, bội chung nhỏ nhất của hai hoặc ba số tự nhiên; thực hiện được phép cộng, phép trừ phân số bằng cách sử dụng ước chung lớn nhất, bội chung nhỏ nhất. – Vận dụng được kiến thức số học vào giải quyết những vấn đề thực tiễn (đơn giản, quen thuộc) (ví dụ: tính toán tiền hay lượng hàng hoá khi mua sắm, xác định số đồ vật cần thiết để sắp xếp chúng theo những quy tắc cho trước,...). |
|||
|
Vận dụng cao: – Vận dụng được kiến thức số học vào giải quyết những vấn đề thực tiễn (phức hợp, không quen thuộc). |
|||
|
2 |
Số nguyên |
Số nguyên âm và tập hợp các số nguyên. Thứ tự trong tập hợp các số nguyên |
Nhận biết: – Nhận biết được số nguyên âm, tập hợp các số nguyên. – Nhận biết được số đối của một số nguyên. – Nhận biết được thứ tự trong tập hợp các số nguyên. – Nhận biết được ý nghĩa của số nguyên âm trong một số bài toán thực tiễn. |
|
Thông hiểu: – Biểu diễn được số nguyên trên trục số. – So sánh được hai số nguyên cho trước. |
|||
|
Các phép tính với số nguyên. Tính chia hết trong tập hợp các số nguyên |
Nhận biết : – Nhận biết được quan hệ chia hết, khái niệm ước và bội trong tập hợp các số nguyên. |
||
|
Vận dụng: – Thực hiện được các phép tính: cộng, trừ, nhân, chia (chia hết) trong tập hợp các số nguyên. – Vận dụng được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng, quy tắc dấu ngoặc trong tập hợp các số nguyên trong tính toán (tính viết và tính nhẩm, tính nhanh một cách hợp lí). – Giải quyết được những vấn đề thực tiễn (đơn giản, quen thuộc) gắn với thực hiện các phép tính về số nguyên (ví dụ: tính lỗ lãi khi buôn bán,...). |
|||
|
Vận dụng cao: – Giải quyết được những vấn đề thực tiễn (phức hợp, không quen thuộc) gắn với thực hiện các phép tính về số nguyên. |
|||
|
3 |
Phân số |
Phân số. Tính chất cơ bản của phân số. So sánh phân số |
Nhận biết: – Nhận biết được phân số với tử số hoặc mẫu số là số nguyên âm. – Nhận biết được khái niệm hai phân số bằng nhau và nhận biết được quy tắc bằng nhau của hai phân số. – Nêu được hai tính chất cơ bản của phân số. – Nhận biết được số đối của một phân số. – Nhận biết được hỗn số dương. |
|
Thông hiểu: – So sánh được hai phân số cho trước. |
|||
|
Các phép tính với phân số |
Vận dụng: – Thực hiện được các phép tính cộng, trừ, nhân, chia với phân số. – Vận dụng được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng, quy tắc dấu ngoặc với phân số trong tính toán (tính viết và tính nhẩm, tính nhanh một cách hợp lí). – Tính được giá trị phân số của một số cho trước và tính được một số biết giá trị phân số của số đó. – Giải quyết được một số vấn đề thực tiễn (đơn giản, quen thuộc) gắn với các phép tính về phân số (ví dụ: các bài toán liên quan đến chuyển động trong Vật lí,...). |
||
|
Vận dụng cao: – Giải quyết được một số vấn đề thực tiễn (phức hợp, không quen thuộc) gắn với các phép tính về phân số. |
|||
|
4 |
Số thập phân |
Số thập phân và các phép tính với số thập phân. Tỉ số và tỉ số phần trăm |
Nhận biết: – Nhận biết được số thập phân âm, số đối của một số thập phân. |
|
Thông hiểu: – So sánh được hai số thập phân cho trước. |
|||
|
Vận dụng: – Thực hiện được các phép tính cộng, trừ, nhân, chia với số thập phân. – Vận dụng được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng, quy tắc dấu ngoặc với số thập phân trong tính toán (tính viết và tính nhẩm, tính nhanh một cách hợp lí). – Thực hiện được ước lượng và làm tròn số thập phân. – Tính được tỉ số và tỉ số phần trăm của hai đại lượng. – Tính được giá trị phần trăm của một số cho trước, tính được một số biết giá trị phần trăm của số đó. – Giải quyết được một số vấn đề thực tiễn (đơn giản, quen thuộc) gắn với các phép tính về số thập phân, tỉ số và tỉ số phần trăm (ví dụ: các bài toán liên quan đến lãi suất tín dụng, liên quan đến thành phần các chất trong Hoá học,...). |
|||
|
Vận dụng cao: – Giải quyết được một số vấn đề thực tiễn (phức hợp, không quen thuộc) gắn với các phép tính về số thập phân, tỉ số và tỉ số phần trăm. |
|||
|
HÌNH HỌC VÀ ĐO LƯỜNG |
|||
|
HÌNH HỌC TRỰC QUAN |
|||
|
1 |
Các hình phẳng trong thực tiễn |
Tam giác đều, hình vuông, lục giác đều |
Nhận biết: – Nhận dạng được tam giác đều, hình vuông, lục giác đều. |
|
Thông hiểu: – Mô tả được một số yếu tố cơ bản (cạnh, góc, đường chéo) của: tam giác đều (ví dụ: ba cạnh bằng nhau, ba góc bằng nhau); hình vuông (ví dụ: bốn cạnh bằng nhau, mỗi góc là góc vuông, hai đường chéo bằng nhau); lục giác đều (ví dụ: sáu cạnh bằng nhau, sáu góc bằng nhau, ba đường chéo chính bằng nhau). |
|||
|
Vận dụng – Vẽ được tam giác đều, hình vuông bằng dụng cụ học tập. – Tạo lập được lục giác đều thông qua việc lắp ghép các tam giác đều. |
|||
|
Hình chữ nhật, hình thoi, hình bình hành, hình thang cân |
Nhận biết – Mô tả được một số yếu tố cơ bản (cạnh, góc, đường chéo) của hình chữ nhật, hình thoi, hình bình hành, hình thang cân. |
||
|
Thông hiểu – Vẽ được hình chữ nhật, hình thoi, hình bình hành bằng các dụng cụ học tập. – Giải quyết được một số vấn đề thực tiễn (đơn giản, quen thuộc) gắn với việc tính chu vi và diện tích của các hình đặc biệt nói trên (ví dụ: tính chu vi hoặc diện tích của một số đối tượng có dạng đặc biệt nói trên,...). |
|||
|
Vận dụng – Giải quyết được một số vấn đề thực tiễn gắn với việc tính chu vi và diện tích của các hình đặc biệt nói trên. |
|||
|
2 |
Tính đối xứng của hình phẳng trong thế giới tự nhiên |
Hình có trục đối xứng |
Nhận biết: – Nhận biết được trục đối xứng của một hình phẳng. – Nhận biết được những hình phẳng trong tự nhiên có trục đối xứng (khi quan sát trên hình ảnh 2 chiều). |
|
Hình có tâm đối xứng |
Nhận biết: – Nhận biết được tâm đối xứng của một hình phẳng. – Nhận biết được những hình phẳng trong thế giới tự nhiên có tâm đối xứng (khi quan sát trên hình ảnh 2 chiều). |
||
|
Vai trò của đối xứng trong thế giới tự nhiên |
Nhận biết: – Nhận biết được tính đối xứng trong Toán học, tự nhiên, nghệ thuật, kiến trúc, công nghệ chế tạo,... – Nhận biết được vẻ đẹp của thế giới tự nhiên biểu hiện qua tính đối xứng (ví dụ: nhận biết vẻ đẹp của một số loài thực vật, động vật trong tự nhiên có tâm đối xứng hoặc có trục đối xứng). |
||
|
HÌNH HỌC PHẲNG |
|||
|
3 |
Các hình hình học cơ bản |
Điểm, đường thẳng, tia |
Nhận biết: – Nhận biết được những quan hệ cơ bản giữa điểm, đường thẳng: điểm thuộc đường thẳng, điểm không thuộc đường thẳng; tiên đề về đường thẳng đi qua hai điểm phân biệt. – Nhận biết được khái niệm hai đường thẳng cắt nhau, song song. – Nhận biết được khái niệm ba điểm thẳng hàng, ba điểm không thẳng hàng. – Nhận biết được khái niệm điểm nằm giữa hai điểm. – Nhận biết được khái niệm tia. |
|
Đoạn thẳng. Độ dài đoạn thẳng |
Nhận biết: – Nhận biết được khái niệm đoạn thẳng, trung điểm của đoạn thẳng, độ dài đoạn thẳng. |
||
|
Góc. Các góc đặc biệt. Số đo góc |
Nhận biết: – Nhận biết được khái niệm góc, điểm trong của góc (không đề cập đến góc lõm). – Nhận biết được các góc đặc biệt (góc vuông, góc nhọn, góc tù, góc bẹt). – Nhận biết được khái niệm số đo góc. |
||
|
MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC SUẤT |
|||
|
1 |
Thu thập và tổ chức dữ liệu |
Thu thập, phân loại, biểu diễn dữ liệu theo các tiêu chí cho trước |
Nhận biết: – Nhận biết được tính hợp lí của dữ liệu theo các tiêu chí đơn giản. |
|
Vận dụng: – Thực hiện được việc thu thập, phân loại dữ liệu theo các tiêu chí cho trước từ những nguồn: bảng biểu, kiến thức trong các môn học khác. |
|||
|
Mô tả và biểu diễn dữ liệu trên các bảng, biểu đồ |
Nhận biết: – Đọc được các dữ liệu ở dạng: bảng thống kê; biểu đồ tranh; biểu đồ dạng cột/cột kép (column chart). |
||
|
Thông hiểu: – Mô tả được các dữ liệu ở dạng: bảng thống kê; biểu đồ tranh; biểu đồ dạng cột/cột kép (column chart). |
|||
|
Vận dụng: – Lựa chọn và biểu diễn được dữ liệu vào bảng, biểu đồ thích hợp ở dạng: bảng thống kê; biểu đồ tranh; biểu đồ dạng cột/cột kép (column chart). |
|||
|
2 |
Phân tích và xử lí dữ liệu |
Hình thành và giải quyết vấn đề đơn giản xuất hiện từ các số liệu và biểu đồ thống kê đã có |
Nhận biết: – Nhận biết được mối liên quan giữa thống kê với những kiến thức trong các môn học trong Chương trình lớp 6 (ví dụ: Lịch sử và Địa lí lớp 6, Khoa học tự nhiên lớp 6,...) và trong thực tiễn (ví dụ: khí hậu, giá cả thị trường,...). |
|
Thông hiểu: – Nhận ra được vấn đề hoặc quy luật đơn giản dựa trên phân tích các số liệu thu được ở dạng: bảng thống kê; biểu đồ tranh; biểu đồ dạng cột/cột kép (column chart). |
|||
|
Vận dụng: – Giải quyết được những vấn đề đơn giản liên quan đến các số liệu thu được ở dạng: bảng thống kê; biểu đồ tranh; biểu đồ dạng cột/cột kép (column chart). |
|||
|
3 |
Một số yếu tố xác suất |
Làm quen với một số mô hình xác suất đơn giản. Làm quen với việc mô tả xác suất (thực nghiệm) của khả năng xảy ra nhiều lần của một sự kiện trong một số mô hình xác suất đơn giản |
Nhận biết: – Làm quen với mô hình xác suất trong một số trò chơi, thí nghiệm đơn giản (ví dụ: ở trò chơi tung đồng xu thì mô hình xác suất gồm hai khả năng ứng với mặt xuất hiện của đồng xu, ...).
|
|
Thông hiểu: – Làm quen với việc mô tả xác suất (thực nghiệm) của khả năng xảy ra nhiều lần của một sự kiện trong một số mô hình xác suất đơn giản. |
|||
|
Mô tả xác suất (thực nghiệm) của khả năng xảy ra nhiều lần của một sự kiện trong một số mô hình xác suất đơn giản |
Vận dụng: – Sử dụng được phân số để mô tả xác suất (thực nghiệm) của khả năng xảy ra nhiều lần thông qua kiểm đếm số lần lặp lại của khả năng đó trong một số mô hình xác suất đơn giản. |
||
....
>> Tải file để tham khảo trọn bộ tài liệu hướng dẫn xây dựng ma trận đề kiểm tra môn Toán THCS
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: