Hệ số góc của đường thẳng: Cách tính và bài tập Cách tính hệ số góc của đường thẳng

Giới thiệu Tải về Bình luận

Hệ số góc của đường thẳng là một trong những kiến thức cơ bản trong chương trình Toán lớp 9 hiện hành và thường xuất hiện trong các bài thi vào 10 môn Toán. Hệ số góc của đường thẳng liên quan đến cả đại số và hình học.

Cách tính hệ số góc của đường thẳng tổng hợp toàn bộ kiến thức về khái niệm, cách tính hệ số góc kèm theo một số bài tập có đáp án giải chi tiết và tự luyện. Qua đó giúp các bạn học sinh tham khảo, hệ thống lại kiến thức để giải nhanh các bài tập về tính hệ số góc của đường thẳng. Ngoài ra để nâng cao kiến thức môn Toán thật tốt các bạn xem thêm một số tài liệu như: chứng minh phương trình luôn có nghiệm với mọi m, chuyên đề Giải phương trình bậc 2 chứa tham số, bài tập hệ thức Vi-et và các ứng dụng.

Hệ số góc của đường thẳng: Cách tính và bài tập

I. Hệ số góc của đường thẳng là gì?
II. Cách tính hệ số góc của đường thẳng
III. Bài tập hệ số góc của đường thẳng y = ax + b
IV. Ứng dụng chuyên đề trong thực tế

I. Hệ số góc của đường thẳng là gì?

Định nghĩa 1: Hệ số góc của đường thẳng $y=a x+b(a \neq 0)$ $y=a x+b(a \neq 0)$ là hệ số của góc tạo thành $(\alpha)$ $(\alpha)$ khi đường thẳng cắt trục hoành $x^{\prime} O x$ $x^{\prime} O x$ tại một điểm và hợp với trục hoành $x^{\prime} O x$ $x^{\prime} O x$ tạo thành một góc. Vì a trong phương trình hàm số có liên quan đến góc này nên a được gọi là hệ số góc của đường thẳng y=a x+b.

Đường thẳng y=a x+b đi qua điểm $M\left(x_{0} ; y_{0}\right)$ $M\left(x_{0} ; y_{0}\right)$ và có hệ số góc a có phương trình là $y=a\left(x-x_{0}\right)+y_{0}$ $y=a\left(x-x_{0}\right)+y_{0}$

Định nghĩa 2:

Đường thẳng không song song với trục tung có hệ số góc (slope) miêu tả độ dốc của đường thẳng và được định nghĩa là tỷ lệ sự thay đổi theo y so với sự thay đổi theo x của hai điểm bất kỳ nằm trên đường thẳng.

Như vậy nếu như đường thẳng đi qua hai điểm (x₁, y₁) và (x₂, y₂) thì hệ số góc của đường thẳng đó sẽ được tính bằng công thức (x₁ khác x₂).

II. Cách tính hệ số góc của đường thẳng

1. Góc tạo bởi đường thằng y = ax + b (a ≠ 0) với trục Ox

Gọi A là giao điểm của đường thẳng y = ax + b với trục Ox và M là một điểm thuộc đường thẳng, nằm phía trên trục Ox. Khi đó $\widehat{MAx}$ $\widehat{MAx}$ là góc tạo bởi đường thẳng y = ax + b với trục Ox.

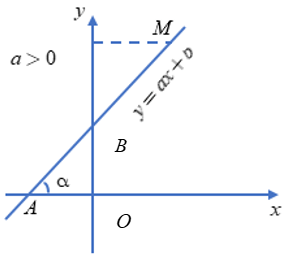
Trường hợp a > 0

+ Với a > 0, góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn và nếu a càng lớn thì góc đó càng lớn.

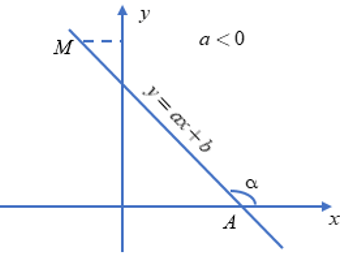
Trường hợp a < 0

+ Với a < 0 góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù và nếu a càng bé thì góc đó càng lớn.

2. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

+ Góc tạo bởi đường thẳng y = ax + b và trục Ox phụ thuộc vào hệ số a. Người ta gọi a là hệ số góc của đường thẳng y = ax + b.

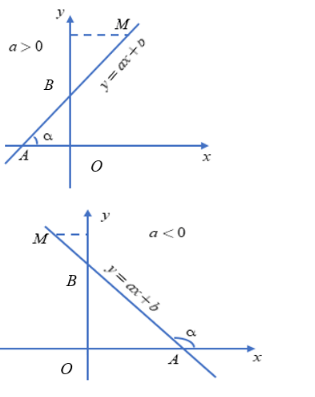
Chú ý:

Ta có điểm A nằm trên trục hoành nên y = 0 và x = $\frac{-b}{a}$ $\frac{-b}{a}$. Vậy tọa độ điểm A là A( $\frac{-b}{a}$ $\frac{-b}{a}$; 0) và độ dài đoạn OA = $\left| {\frac{{ - b}}{a}} \right|$ $\left| {\frac{{ - b}}{a}} \right|$.

Ta có điểm B nằm trên trục tung nên x = 0 và y = b. Vậy tọa độ điểm B là B(0; b) và độ dài đoạn OB = |b|.

+ Với a > 0, ta có: $\tan \widehat{MAx} = \frac{{OB}}{{OA}} = \frac{{\left| b \right|}}{{\left| {\frac{{ - b}}{a}} \right|}} = \left| a \right| = a$ $\tan \widehat{MAx} = \frac{{OB}}{{OA}} = \frac{{\left| b \right|}}{{\left| {\frac{{ - b}}{a}} \right|}} = \left| a \right| = a$

Từ đó dùng bảng lượng giác hoặc máy tính bỏ túi suy ra số đo của $\widehat{MAx}$ $\widehat{MAx}$

+ Khi a < 0 ta có:

$\tan \left( {{{180}^0} - \widehat {MAx}} \right) = \tan \widehat {OAB} = \frac{{OB}}{{OA}} = \frac{{\left| b \right|}}{{\left| {\frac{{ - b}}{a}} \right|}} = \left| a \right| = - a$ $\tan \left( {{{180}^0} - \widehat {MAx}} \right) = \tan \widehat {OAB} = \frac{{OB}}{{OA}} = \frac{{\left| b \right|}}{{\left| {\frac{{ - b}}{a}} \right|}} = \left| a \right| = - a$ (do a < 0)

Từ đó tìm số đo của góc (180° - $\widehat{MAx}$ $\widehat{MAx}$), sau đó suy ra $\widehat{MAx}$ $\widehat{MAx}$.

+ Các đường thẳng có cùng hệ số a (a là hệ số của x) thì tạo với trục Ox các góc bằng nhau.

+ Khi b = 0, ta có hàm số y = ax. Trong trường hợp này, ta có thể nói a là hệ số góc của đường thẳng y = ax

III. Bài tập hệ số góc của đường thẳng y = ax + b

A. Một số bài có đáp án

Câu 1: Cho hàm số y = x + 2. Tính góc tạo bởi đường thẳng y = x + 2 với trục Ox (làm tròn đến phút).

Hướng dẫn:

Tìm giao điểm A giữa đường thẳng y = x + 2 với trục Ox.

Tìm giao điểm B giữa đường thẳng y = x + 2 với trục Oy.

Gợi ý đáp án

Vẽ đồ thị hàm số y = x + 2

Đồ thị hàm số đã cho đi qua hai điểm A(0; 2); B(-2; 0).

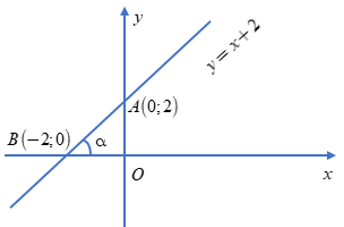
Gọi góc tạo bởi đường thẳng y = x + 2 với trục Ox là α, ta có $\widehat{ABO}$ $\widehat{ABO}$ = α Xét tam giác vuông OAB , ta có $\tan \alpha = \frac{{OA}}{{OB}} = \frac{2}{2} = 1$ $\tan \alpha = \frac{{OA}}{{OB}} = \frac{2}{2} = 1$ (1 chính là hệ số góc của đường thẳng y = x + 2)

Khi đó số đo góc α là α = 45⁰

Câu 2: Cho (d): y = ax + b. Tìm a, b biết (d) đi qua gốc tọa độ và song song với (d') trong đó (d') có hệ số góc bằng 1.

Hướng dẫn:

Hai đường thẳng song song với nhau thì hai đường thẳng có hệ số góc bằng nhau.

Gợi ý đáp án

Theo bài ta, (d) đi qua gốc tọa độ nên ta có b = 0

(d) song song với (d') và (d') có hệ số góc bằng 1 nên a = 1

Vậy a = 1, b = 0.

Câu 3

Tìm hàm số bậc nhất có đồ thị là đường thẳng đi qua điểm (1;-2) và có hệ số góc là 3

Gợi ý đáp án

Vì hàm số có hệ số góc là 3 => $y=3x+b$

hàm số bậc nhất có đồ thị là đường thẳng đi qua điểm (1;-2) , thay $x=1$, $y=-2$ => $b=-5$

Vậy ta có hàm số là $y=3x-5$

Câu 4

Tìm hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc là -2 và cắt trục hoành tại điểm có hoành độ bằng 3

Gợi ý đáp án

Vì hàm số bậc nhất có đồ thị là đường thẳng có hệ số góc là -2 => $y=-2x+b$

Đường thẳng cắt trục hoành tại điểm có hoành độ bằng 3 => Đường thẳng đi qua điểm (3;0)

Thay x=3; y=0 ta có: $0=-2.3+b$ => b= 6

Vậy ta có hàm số $y=-2x+6$

Câu 5

Hãy chỉ ra cặp đường thẳng song song với nhau và các cặp đường thẳng cắt nhau trong các đường thẳng sau

a) $y=-x+1$; $y=-2x+1$

c) $y=-2x+2$ $y=-x$

Gợi ý đáp án

Các cặp song song là: $y=-x+1$ và $y=-x$; $y=-2x+1$ và $y=-2x+2$

Các cặp cắt nhau là: $y=-x+1$ và $y=-2x+2$; $y=-x$ và $y=-2x+1$; $y=-x+1$ và $y=-2x+1$; $y=-x$ và $y=-2x+2$

Câu 6

Cho hàm số bậc nhất $y=mx-5$ và $y=(2m+1)x+3$. Tìm các giá trị của m để đồ thị của hai hàm số là:

a) Hai đường thẳng song song

b) Hai đường thẳng cắt nhau

Gợi ý đáp án

a) Hai đường thẳng song song khi $a=a'$ => $m=2m+1$ => $m=-1$

b) Hai đường thẳng cắt nhau khi $a\neq a$ $a\neq a'$ => $m\neq 2m+1$ $m\neq 2m+1$ => $m\neq -1$ $m\neq -1$

Câu 7

Tìm hàm số bậc nhất có đồ thị là đường thẳng song song với đường thẳng $y=-3x+1$ và đi qua điểm (2;6)

Gợi ý đáp án

Vì hàm số song song với đường thẳng $y=-3x+1$ => $a=-3$

Vì hàm số là đường thẳng đi qua điểm (2;6). Thay $x=2$, $y=6$ ta có: $6=-3.2+b$ => $b=12$

Vậy hàm số cần tìm là $y=-3x+12$

B. Một số bài tự luyện

Câu 1: Cho hàm số y = 2x + 2 có đồ thị là đường thẳng (d)

a) Hãy xác định hệ số góc của đường thẳng (d)

b) Vẽ đồ thị của hàm số

c) Đường thắng (d) có đi qua điểm A (-4;6) không? Vì sao?

Câu 2: Cho đường thẳng d: ax + (2a - 1)y + 3 = 0. Tìm a để đường thẳng d đi qua điểm M (1;-1). Khi đó hãy tìm hệ số góc của đường thẳng d.

Câu 3: Xác định hệ số góc k của đường thẳng y = kx + 3 - k trong mỗi trường hợp dưới đây:

a) Đường thẳng song song với đồ thị hàm số y = $\frac{2}{3}$ $\frac{2}{3}$x.

b) Đường thẳng cắt trục tung tại điểm có tung độ bằng 2.

c) Đường thẳng cắt trục hoành tại điểm có hoành độ bằng 3.

Câu 4;

Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng $y=x$ và $y=-x+2$

a) Vẽ hai đường thẳng đã cho trên cùng một mặt phẳng tọa độ

b) Tìm giao điểm A của hai đường thẳng đã cho

c) Gọi B là giao điểm của đường thẳng $y=-x+2$ và trục Ox. Chứng minh tam giác OAB vuông tại A, tức hai đường thẳng $y=x$ và $y=-x+2$ vuông góc với nhau

d) Có nhận xét gì về tích hai hệ số góc của hai đường thẳng đã cho

IV. Ứng dụng chuyên đề trong thực tế

Cũng như nhiều kiến thức toán học thú vị khác, nội dung này cũng được ứng dụng hết sức hiệu quả trong những công việc ở thực tế đời sống. Cụ thể, chủ đề này thường được ứng dụng trong Chọn chiến lược kinh doanh, nhằm xác định chiến lược mang lại mức lợi nhuận cao nhất cho công ty của mình; hay còn được ứng dụng trong Tốc độ hội tụ, giải quyết các vấn đề thực tế….

Chia sẻ bởi: