Toán 12 Bài 2: Toạ độ của vectơ trong không gian Giải Toán 12 Chân trời sáng tạo trang 52→57

Giải Toán lớp 12 tập 1 trang 56, 57 Chân trời sáng tạo là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 12 tham khảo.

Giải Toán 12 Chân trời sáng tạo bài 2 Toạ độ của vectơ trong không gian được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 56, 57. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán 12 tập 1 bài 2 Toạ độ của vectơ trong không gian, mời các bạn cùng theo dõi tại đây.

Giải bài tập Toán 12 trang 56, 57 Tập 1

Bài 1 trang 56 SGK Toán 12 tập 1

Trong không gian Oxyz, biết:

a) \(\overrightarrow{a}=5\overrightarrow{i}+7\overrightarrow{j}-3\overrightarrow{k},\ \overrightarrow{b}=2\overrightarrow{i}+4\overrightarrow{k\ }\). Tìm toạ độ các vectơ \(\overrightarrow{a},\overrightarrow{b\ }\)

b) \(\overrightarrow{OM}=4\overrightarrow{i}-\overrightarrow{j}+3\overrightarrow{k},\ \overrightarrow{ON}=8\overrightarrow{i}-5\overrightarrow{j\ }\). Tìm toạ độ các điểm M, N.

Hướng dẫn giải:

a) Ta có:

\(\overrightarrow{a}=5\overrightarrow{i}+7\overrightarrow{j}-3\overrightarrow{k}\) nên \(\overrightarrow{a}=\left(5;7;-3\right)\)

\(\overrightarrow{b}=2\overrightarrow{i}+4\overrightarrow{k\ }\) nên \(\overrightarrow{b}=\left(2;0;4\right)\)

b) Ta có:

\(\overrightarrow{OM}=4\overrightarrow{i}-\overrightarrow{j}+3\overrightarrow{k\ }\) nên M(4; - 1; 3)

\(\overrightarrow{ON}=8\overrightarrow{i}-5\overrightarrow{j\ \ }\) nên N(8; - 5; 0)

Bài 2 trang 56 SGK Toán 12 tập 1

Trong không gian Oxyz, biết:

a) \(\overrightarrow{a}=(-2;5;-7),\overrightarrow{b}=(4;0;1)\). Tính \(\overrightarrow{a},\overrightarrow{b}\), theo các vectơ \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k\ }\)

b) A(7; –2; 1), B(0; 5; 0). Tính \(\overrightarrow {OA} , \overrightarrow {OB}\) theo các vectơ \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k\ }\)

Hướng dẫn giải:

a) Ta có:

\(\overrightarrow{a}=-2\overrightarrow{i}+5\overrightarrow{j}-7\overrightarrow{k\ }\)

\(\overrightarrow{b}=4\overrightarrow{i}+\overrightarrow{k\ }\)

b) \(\overrightarrow{OA}=7\overrightarrow{i}-2\overrightarrow{j}+\overrightarrow{k\ }\)

\(\overrightarrow{OB}=5\overrightarrow{j}\)

Bài 3 trang 56 SGK Toán 12 tập 1

Cho tứ diện SABC có ABC là tam giác vuông tại B, BC = 3, BA = 2, SA vuông góc với mặt phẳng (ABC) và có độ dài bằng 2 (Hình 13).

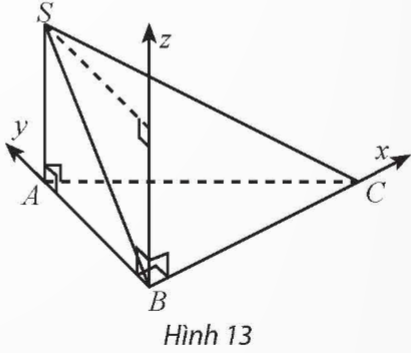
a) Xác định một hệ toạ độ dựa trên gợi ý của hình vẽ và chỉ ra các vectơ đơn vị trên các trục toạ độ.

b) Tìm toạ độ các điểm A, B, C, S.

Hướng dẫn giải:

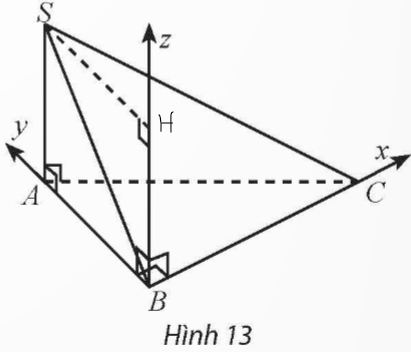
a) Chọn hệ trục tọa độ Oxyz với gốc O trùng với điểm B.

Các vectơ đơn vị trên ba trục Ox, Oy, Oz lần lượt là \(\overrightarrow{BC},\overrightarrow{BA},\overrightarrow{BH\ }\)

b) A(0; 2; 0); B(0; 0; 0); C(3; 0; 0); S(0; 2; 2)

Bài 4 trang 57 SGK Toán 12 tập 1

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2, SA vuông góc với đáy và SA bằng 1 (Hình 14). Thiết lập hệ toạ độ như hình vẽ, hãy vẽ các vectơ đơn vị trên các trục Ox, Oy, Oz và tìm toạ độ các điểm A, B, C, S.

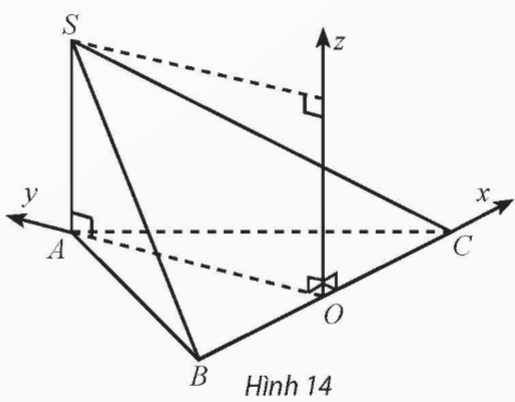
Hướng dẫn giải:

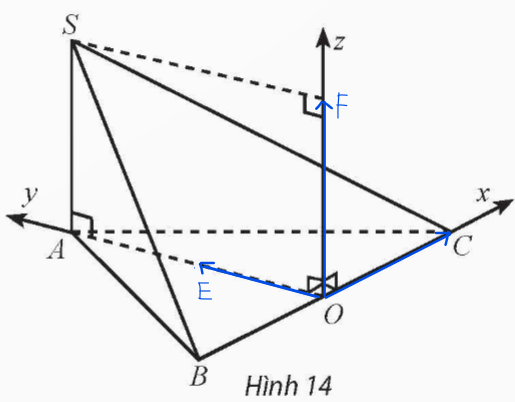
Vẽ điểm E thuộc Oy sao cho OE = 1 và F thuộc Oz sao cho OF = 1.

Các vectơ đơn vị trên các trục Ox, Oy, Oz lần lượt là \(\overrightarrow{OC},\overrightarrow{OE},\overrightarrow{OF}\)

Ta có: \(OA=\sqrt{AB^2-OB^2}=\sqrt{2^2-1^2}=\sqrt{3}\)

Vậy \(A\left(0;\sqrt{3};0\right),\ B\left(-1;0;0\right),\ C\left(1;\ 0;\ 0\right),\ S\left(0;\sqrt{3};1\right)\)

Bài 5 trang 57 SGK Toán 12 tập 1

Hướng dẫn giải:

Do ABCD là hình thoi nên AC vuông góc với BD

Suy ra OA = OC = 4 và OB = OD = \(\sqrt{5^2-4^2}\) = 3

Ta có: A(0; - 4; 0); B(3; 0; 0); C(0; 4; 0); S(0; 0; 4)

M là trung điểm của SC nên M có tọa độ là M(0; 2; 2)

Vậy \(\overrightarrow{AB}=\left(3;4;0\right);\ \overrightarrow{AC}=\left(0;8;0\right)\)

\(\overrightarrow{AS}=\left(0;4;4\right);\ \overrightarrow{AM}=\left(0;6;2\right)\)

Bài 6 trang 57 SGK Toán 12 tập 1

Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ toạ độ Oxyz như Hình 16 với độ dài đơn vị trên các trục toạ độ bằng 1 m. Tìm toạ độ của vectơ \(\overrightarrow {AB}\).

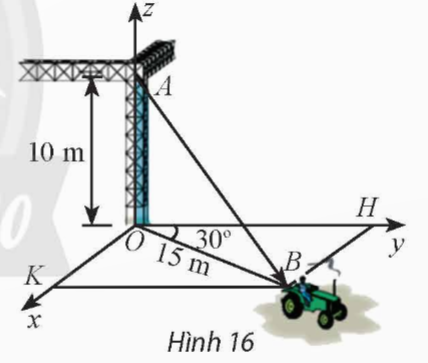
Hướng dẫn giải:

Xét tam giác ABH vuông tại H, ta có:

BH = OB. sin 30o = 15 . sin 30o = \(\frac{15}{2}\) m

BK = OH = OB. cos 30o

= 15 . cos 30o = \(\frac{15\sqrt{3}}{2}\)

Do đó \(A\left(0;\ 0;\ 10\right),\ B\left(\frac{15}{2};\frac{15\sqrt{3}}{2};0\right)\)

Vậy \(\overrightarrow{AB}\left(\frac{15}{2};\frac{15\sqrt{3}}{2};-10\right)\).

Bài 7 trang 57 SGK Toán 12 tập 1

Ở một sân bay, ví trí của máy bay được xác định bởi điểm M trong không gian Oxyz như Hình 17. Gọi H là hình chiếu vuông góc của M xuống mặt phẳng (Oxy). Cho biết OM = 50, \((\overrightarrow{i};\overrightarrow{OH})=64^{\circ},(\overrightarrow{OH};\overrightarrow{OM})=48^{\circ}\). Tìm toạ độ của điểm M.

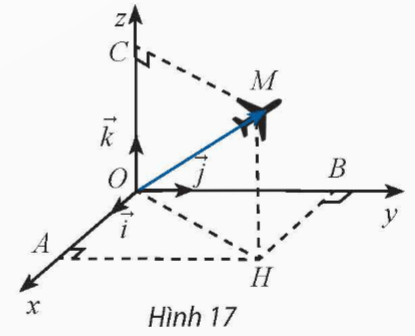
Hướng dẫn giải:

\((\overrightarrow{i};\overrightarrow{OH})=\widehat{AOH}=64^{\circ},(\overrightarrow{OH};\overrightarrow{OM})=\widehat{MOH}=48^{\circ}\)

Xét tam giác OHM vuông tại H, ta có:

MH = OM . sin MOH

= 50 . sin 48o ≈ 37,2 m

OH = OM . cos MOH

= 50 . cos 48o ≈ 33,5 m

Xét tam giác OAH vuông tại A, ta có:

OA = OH . cos AOH

= 33,5 . cos 64o ≈ 14,7 m

AH = OH . sin AOH

= 33,5 . sin 64o ≈ 30,1 m

Vậy M(14,7; 30,1; 37,2).