Download.vn Học tập Lớp 12 Thi THPT Quốc Gia Toán

Bộ đề ôn thi THPT Quốc gia môn Toán năm 2023 (40 đề + đáp án) Ôn thi THPT Quốc gia 2023 môn Toán

Giới thiệu Tải về Bình luận
  • 157

Bộ đề ôn thi THPT Quốc gia môn Toán năm 2023 gồm 40 đề ôn luyện có đáp án kèm theo ở cuối mỗi đề ôn. Đây là tài liệu học tập hữu ích cho quá trình ôn luyện trong kì thi THPT Quốc Gia sắp tới.

TOP 40 Đề ôn Toán THPT Quốc gia 2023 giúp các em có thể học tập và ôn luyện thật tốt các câu hỏi trọng tâm thường xuất hiện trong các bài thi. Qua đó nắm bắt đúng trọng tâm của chương trình Toán lớp 12. Bên cạnh đó các em xem thêm cấu trúc đề thi THPT Quốc gia môn Toán, đề thi minh họa THPT Quốc gia môn Toán.

TOP 40 Đề ôn thi THPT Quốc gia 2023 môn Toán

Xem Đề thi THPT Quốc gia 2022 môn Toán (chính thức)

Câu 1: Phần thực và phần ảo của số phức z=(1+2 i) i lần lượt là

A. 1 và -2 .
B. 2 và 1 .
c. 1 và 2 .
D. -2 và 1 .

Câu 2. Trong không gian O x y z, mặt phẳng (P): 3 x-2 z-1=0 có một vectơ pháp tuyến là

A. \vec{u}=(3 ;-2 ; 0).
B. \vec{u}=(3 ;-2 ;-1).
C. \vec{u}=(3 ; 0 ; 2).
D. \vec{u}=(-3 ; 0 ; 2).

Câu 3. Cho cấp số nhân \left(u_n\right) với u_1=-2 và q=-5. Viết bốn số hạng đầu tiên của cấp số nhân.

A. -2 ; 10 ; 50 ; 250.
B. -2 ; 10 ; 50 ;-250.
C. -2 ; 10 ;-50 ; 250.
D. -2 ;-10 ;-50 ;-250.

Câu 4

Cho số phức z có biểu diễn hình học là diếm M ở hình vē bền. Khẳng định nào sau đây là đúng?

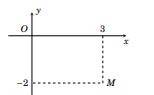
A. z=-3-2 i.
B. z=3+2 i.
C. z=-9+2 i.
D. z=3-2 i.

Câu 5. Cho số phức z thỏa mān z-i(4-2 i)=8 i-6. Phần thực của số phức z bằng

A. 8.
B. 12.
c. -4 .
D. -8 .

Câu 6. Tính thế tích của khối lập phương có cạnh 2 a.

A. 4 a^3.
B. a^3.
c. 2 a^3.
D. 8 a^3.

Câu 7 Trong mặt phẳng có 10 điểm phân biệt. Số vectơ khác vectơ không được tạo thành là

A. 90 .
B. 2^{10}.
C. 45 .
D. 10 .

Câu 8 Tinh \int_0^1 3^{2 x+1} \mathrm{~d} x bằng

A. \frac{12}{\ln 3}.
B. \frac{4}{\ln 3}
c. \frac{27}{\ln 9}.
D. \frac{9}{\ln 9}.

Câu 9

Đồ thị của hàm số nào có dạng như đường cong trong hình vē dưới đây?

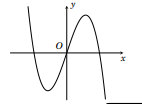
A. y=x^3-3 x.
B. y=3 x^4-2 x^2.
C. y=-x^3+3 x.
D. y=-x^4+3 x^2.

................

Chia sẻ bởi: 👨 Trịnh Thị Thanh
157
  • Lượt tải: 58.852
  • Lượt xem: 288.625
  • Dung lượng: 4,2 MB
Tìm thêm: Ôn thi THPT Quốc gia 2022 môn Toán Toán 12
Sắp xếp theo
Xóa Đăng nhập để Gửi

    Tài liệu tham khảo khác

    Chủ đề liên quan

    Mới nhất trong tuần