Tuyển tập 101 đề thi giữa kì 1 môn Toán 9 Đề kiểm tra giữa học kì 1 lớp 9 môn Toán

Tải về Bình luận

Đề kiểm tra giữa kì 1 Toán 9 tuyển chọn 101 đề thi giữa kì 1 tự luyện nhằm thử sức, kiểm tra kỹ năng và củng cố kiến thức với các phép toán. Thông qua đề thi giữa kì 1 Toán 9 quý thầy cô có thêm nhiều tài liệu tham khảo để ra đề thi cho các em học sinh của mình.

TOP 101 Đề thi Toán 9 giữa kì 1 được biên soạn rất đa dạng gồm cả cấu trúc đề 100% tự luận, 60% tự luận kết hợp 40% trắc nghiệm, 30% trắc nghiệm kết hợp 70% tự luận với mức độ câu hỏi khác nhau. Hi vọng qua tài liệu này sẽ là người bạn đồng hành giúp các em học sinh lớp 9 dễ dàng ôn tập, hệ thống kiến thức, luyện giải đề, rồi so sánh kết quả thuận tiện hơn. Vậy sau đây là trọn bộ 101 đề thi giữa kì 1 Toán 9 mời các bạn cùng theo dõi.

Đề thi Toán giữa kì 1 lớp 9 - Đề 1

Bài 1: (1,5 điểm) Tính:

$a) A=(\sqrt{99}-\sqrt{18}-\sqrt{11}) \cdot \sqrt{11}+3 \sqrt{22}$ $a) A=(\sqrt{99}-\sqrt{18}-\sqrt{11}) \cdot \sqrt{11}+3 \sqrt{22}$

$b) B=\sqrt{4+2 \sqrt{3}}+\sqrt{4-2 \sqrt{3}}$ $b) B=\sqrt{4+2 \sqrt{3}}+\sqrt{4-2 \sqrt{3}}$

$c) C=\frac{5}{\sqrt{7}+\sqrt{2}}-\frac{7-\sqrt{7}}{\sqrt{7}-1}+6 \cdot \sqrt{\frac{1}{2}}$ $c) C=\frac{5}{\sqrt{7}+\sqrt{2}}-\frac{7-\sqrt{7}}{\sqrt{7}-1}+6 \cdot \sqrt{\frac{1}{2}}$

Bài 2. (2,0 điểm). Giải các phương trình sau:

$a) \sqrt{2 x-1}=\sqrt{x+1}$ $a) \sqrt{2 x-1}=\sqrt{x+1}$

$b) \sqrt{4-x^{2}}-x+2=0$ $b) \sqrt{4-x^{2}}-x+2=0$

Bài 3: (2 điểm) Cho biểu thức $A=\frac{\sqrt{a}+1}{\sqrt{a}-3} và B=\frac{2 \sqrt{a}}{\sqrt{a}+3}-\frac{\sqrt{a}}{3-\sqrt{a}}-\frac{3 a+3}{a-9}, \quad(a \geq 0 ; a \neq 9)$ $A=\frac{\sqrt{a}+1}{\sqrt{a}-3} và B=\frac{2 \sqrt{a}}{\sqrt{a}+3}-\frac{\sqrt{a}}{3-\sqrt{a}}-\frac{3 a+3}{a-9}, \quad(a \geq 0 ; a \neq 9)$

a) Tính giá trị của A khi a=16

b) Rút gọn biểu thức $P=\frac{A}{B}.$ $P=\frac{A}{B}.$

c) So sánh P với 1

Bài 4: (3 điểm)

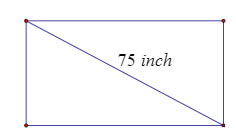
1. (1 điểm) Một chiếc tivi hình chữ nhật màn hình phẳng 75 inch ( đường chéo tivi dài 75 inch) có góc tạo bời chiều rộng và đường chéo là $53^{\circ} 08^{\prime}.$ $53^{\circ} 08^{\prime}.$ Hỏi chiếc tivi ấy có chiều dài, chiều rộng là bao nhiêu cm? Biết 1 inch =2,54 cm. (Kết quả làm tròn đến chữ sổ thập phân thứ nhật)

2. Cho tam giác EMF vuông tại M, đường cao MI. Vẽ $I P \perp M E$ $I P \perp M E$, $(P \in M E) và I Q \perp M F,(Q \in M F)$ $(P \in M E) và I Q \perp M F,(Q \in M F)$

a) Cho biết $M E=4 \mathrm{~cm}, \quad \sin M F E=\frac{3}{4}.$ $M E=4 \mathrm{~cm}, \quad \sin M F E=\frac{3}{4}.$ Tính độ dài các đoạn EF, EI, MI.

b) Chứng minh $M P \cdot P E+M Q \cdot Q F=M I^{2}$ $M P \cdot P E+M Q \cdot Q F=M I^{2}$

Bài 5; Tìm GTNN của biều thức: $A=\sqrt{x^{2}+6 x+9}+\sqrt{x^{2}-2 x+1}$ $A=\sqrt{x^{2}+6 x+9}+\sqrt{x^{2}-2 x+1}$

Đề thi giữa kì 1 Toán 9 - Đề 2

TRƯỜNG THCS………

ĐỀ KIỂM TRA GIỮA HỌC KỲ I
Năm học: 20...– 20...
Môn: Toán 9
Thời gian làm bài: 90 phút

Bài 1: (1 đ) : Tìm điều kiện của x để các căn thức sau có nghĩa.

$a) \quad \sqrt{x-2}$ $a) \quad \sqrt{x-2}$

$b) \sqrt{2-3 x}$ $b) \sqrt{2-3 x}$

Bài 2: Tính : (2 đ)

$A) \sqrt{4.36}$ $A) \sqrt{4.36}$

$b) \sqrt{\frac{25}{81} \cdot \frac{16}{49}}$ $b) \sqrt{\frac{25}{81} \cdot \frac{16}{49}}$

$c) \quad(\sqrt{8}-3 \sqrt{2}) \cdot \sqrt{2}$ $c) \quad(\sqrt{8}-3 \sqrt{2}) \cdot \sqrt{2}$

$d) \frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}$ $d) \frac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}$

Bài 3 : Rút gọn biểu thức : (1 đ)

$a) \sqrt{19+\sqrt{136}}-\sqrt{19-\sqrt{136}}$ $a) \sqrt{19+\sqrt{136}}-\sqrt{19-\sqrt{136}}$

$b) \sqrt[3]{27}+\sqrt[3]{-64}+2 \sqrt[3]{125}$ $b) \sqrt[3]{27}+\sqrt[3]{-64}+2 \sqrt[3]{125}$

Bài 4 : (1 đ) Tìm x, biết

$\sqrt{4 x+20}-2 \sqrt{x+5}+\sqrt{9 x+45}=6$ $\sqrt{4 x+20}-2 \sqrt{x+5}+\sqrt{9 x+45}=6$

Bài 5: Cho biểu thức

$=\left(\frac{1}{x+2 \sqrt{x}}-\frac{1}{\sqrt{x}+2}\right): \frac{1-\sqrt{x}}{x+4 \sqrt{x}+4} \quad$ $=\left(\frac{1}{x+2 \sqrt{x}}-\frac{1}{\sqrt{x}+2}\right): \frac{1-\sqrt{x}}{x+4 \sqrt{x}+4} \quad$ với $x>0 ;$

a) Rút gọn A

b) Tìm x để F = $\frac{5}{2}$ $\frac{5}{2}$

Bài 6 (3 đ): Cho tam giác ABC vuông tại A có đường cao AH chia cạnh huyền BC thành hai đoạn : BH = 4 cm và HC = 6 cm.

a) Tính độ dài các đoạn AH, AB, AC.

b) Gọi M là trung điểm của AC.

Tính số đo góc AMB (làm tròn đến độ).

c) Kẻ AK vuông góc với BM. Chứng minh : BKC ~ D

Đề kiểm tra giữa kì 1 Toán 9 - Đề 3

Bài 1 (2,0 điểm).

1. Thực hiện phép tính.

$a) \sqrt{81}-\sqrt{80} \cdot \sqrt{0,2}$ $a) \sqrt{81}-\sqrt{80} \cdot \sqrt{0,2}$

$b) \sqrt{(2-\sqrt{5})^{2}}-\frac{1}{2} \sqrt{20}$ $b) \sqrt{(2-\sqrt{5})^{2}}-\frac{1}{2} \sqrt{20}$

2. Tìm điều kiện của x để các biểu thức sau có nghĩa:

$a) \sqrt{-x+1}$ $a) \sqrt{-x+1}$

$b) \sqrt{\frac{1}{x^{2}-2 x+1}}$ $b) \sqrt{\frac{1}{x^{2}-2 x+1}}$

Bài 2 (2,0 điểm).

1. Phân tích đa thức thành nhân tử.

$a) a b+b \sqrt{a}+\sqrt{a}+1 \quad$ $a) a b+b \sqrt{a}+\sqrt{a}+1 \quad$với $(a \geq 0)$ $(a \geq 0)$

$4 a+1 \quad$ $4 a+1 \quad$với $(a<0)$

2. Giải phương trình: $\sqrt{9 x+9}+\sqrt{x+1}=20$ $\sqrt{9 x+9}+\sqrt{x+1}=20$

Bài 3 (2,0 điểm).

Cho biểu thức

$A=\left(\frac{1}{x+2 \sqrt{x}}-\frac{1}{\sqrt{x}+2}\right): \frac{1-\sqrt{x}}{x+4 \sqrt{x}+4} \quad$ $A=\left(\frac{1}{x+2 \sqrt{x}}-\frac{1}{\sqrt{x}+2}\right): \frac{1-\sqrt{x}}{x+4 \sqrt{x}+4} \quad$ với $x>0$ và $x \neq 1$ $x \neq 1$

a) Rút gọn biểu thức A.

b) Tìm x để A = $\frac{5}{3}$ $\frac{5}{3}$

Bài 4 (3,5 điểm).

Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm. Tính độ dài các đoạn thẳng AB, AC, AH.

Trên cạnh AC lấy điểm K (K $\neq$ $\neq$ A, K $\neq$ $\neq$ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC

Chứng minh rằng: $S_{B H D}=\frac{1}{4} S_{B K C} \cos ^{2} \widehat{A B D}$ $S_{B H D}=\frac{1}{4} S_{B K C} \cos ^{2} \widehat{A B D}$

Bài 5 (0,5 điểm).

Cho biểu thức $P=x^{3}+y^{3}-3(x+y)+1993$ $P=x^{3}+y^{3}-3(x+y)+1993$

Tính giá trị biểu thức P với: $x=\sqrt[3]{9+4 \sqrt{5}}+\sqrt[3]{9-4 \sqrt{5}}$ $x=\sqrt[3]{9+4 \sqrt{5}}+\sqrt[3]{9-4 \sqrt{5}}$ và $y=\sqrt[3]{3+2 \sqrt{2}}+\sqrt[3]{3-2 \sqrt{2}}$ $y=\sqrt[3]{3+2 \sqrt{2}}+\sqrt[3]{3-2 \sqrt{2}}$

Đề thi giữa kì 1 Toán 9 - Đề 4

Bài 1 (2,5 điểm) Cho biểu thức $P=\left(\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{1}{x-\sqrt{x}}\right):\left(\frac{1}{\sqrt{x}+1}+\frac{2}{x-1}\right)$ $P=\left(\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{1}{x-\sqrt{x}}\right):\left(\frac{1}{\sqrt{x}+1}+\frac{2}{x-1}\right)$

a) Rút gọn biểu thức $\mathrm{P}$ $\mathrm{P}$ với x>0 và $x \neq 1.$ $x \neq 1.$

b) Tìm giá trị của x để P<2.

c) Cho x>9. Tìm giá trị nhỏ nhất của $Q=P \cdot \frac{\sqrt{x}(x+7)}{(\sqrt{x}-3)(x-1)}$ $Q=P \cdot \frac{\sqrt{x}(x+7)}{(\sqrt{x}-3)(x-1)}$

Bài 2 (1,5 điểm) Giải các phương trình sau:

$a) 3+\sqrt{2 x-3}=x$ $a) 3+\sqrt{2 x-3}=x$

$b) \frac{2 \sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}+1}{\sqrt{x}-3}+\frac{3-11 \sqrt{x}}{9-x}=\frac{6}{\sqrt{x}-3}$ $b) \frac{2 \sqrt{x}}{\sqrt{x}+3}+\frac{\sqrt{x}+1}{\sqrt{x}-3}+\frac{3-11 \sqrt{x}}{9-x}=\frac{6}{\sqrt{x}-3}$

Bài 3 ( 2,0 điểm) Cho đường thẳng $(\mathrm{d})$ $(\mathrm{d})$ có phương trình $y=m x+3 m+2 ( \mathrm{m}$ $y=m x+3 m+2 ( \mathrm{m}$ là tham số) và đường thẳng: $\left(d_1\right): y=2 x+4$ $\left(d_1\right): y=2 x+4$

a) Tìm giá trị của m để $(\mathrm{d})$ $(\mathrm{d})$ cắt $\left(d_1\right)$ $\left(d_1\right)$ tại điểm có hoành độ x=1.

b) Với giá trị m tìm được hãy vẽ đường thẳng (d) và tính khoảng cách từ gốc tọa độ đến đường thẳng $(\mathrm{d}).$ $(\mathrm{d}).$

c) Tìm giá trị của m để khoảng cách từ điểm E(-3 ; 0) đến đường thẳng (d) lớn nhất

Bài 4 (3,5 điểm) Từ điểm M ở ngoài đường tròn (O) kẻ 2 tiếp tuyến $\mathrm{MA}, \mathrm{MB}(\mathrm{A}, \mathrm{B}$ $\mathrm{MA}, \mathrm{MB}(\mathrm{A}, \mathrm{B}$ là tiếp điểm). Kẻ đường kính AC.

a) Chứng minh rằng BC / / OM

b) Tiếp tuyến tại C của (O) cắt tia AB tại F. Chứng minh rằng: $A C^2=A B \cdot A F$ $A C^2=A B \cdot A F$

Đề thi giữa kì 1 Toán 9 - Đề 5

Bài 1. (điểm) Cho hai biểu thức: $A=\frac{2 \sqrt{x}-1}{2 \sqrt{x}+1}$ $A=\frac{2 \sqrt{x}-1}{2 \sqrt{x}+1}$ và $B=\frac{2 \sqrt{x}}{\sqrt{x}-1}-\frac{5}{\sqrt{x}+2}-\frac{6}{x+\sqrt{x}-2}$ $B=\frac{2 \sqrt{x}}{\sqrt{x}-1}-\frac{5}{\sqrt{x}+2}-\frac{6}{x+\sqrt{x}-2}$ với $x \geq 0, x \neq 1$ $x \geq 0, x \neq 1$

1. Tính giá trị của biểu thức A khi $x=\frac{9}{4}.$ $x=\frac{9}{4}.$

2. Rút gọn biểu thức B.

3. Tìm x để biểu thức $M=A \cdot B$ $M=A \cdot B$ có giá trị là một số nguyên.

Bài 2. (điểm) Cho hàm số y=(m-1) x-3 (1) (Với m là tham số, $m \neq 1$ $m \neq 1$ )

1. Tìm m để đồ thị hàm số (1) đi qua điểm A(2 ; 1). Với m vừa tìm được, vẽ đồ thị hàm số (1) trong mặt phẳng tọa độ O x y.

2. Tìm m để đồ thị hàm số (1) song song với đường thẳng $y=\left(m^2-3\right) x-m^2+1$ $y=\left(m^2-3\right) x-m^2+1$

3. Tìm m để đồ thị hàm số (1) cắt đường thẳng y=3x tại một điểm nằm trong góc phần tư thứ ba.+2

Đề thi giữa học kì 1 Toán 9 - Đề 6

Câu 1. (2 điểm) Tính giá trị biểu thức:

$1. A=(15 \sqrt{200}-4 \sqrt{450}+2 \sqrt{50}): \sqrt{10}-10 \sqrt{20}.$ $1. A=(15 \sqrt{200}-4 \sqrt{450}+2 \sqrt{50}): \sqrt{10}-10 \sqrt{20}.$

$2. B=\sqrt{(5-3 \sqrt{2})^2}+\sqrt{(\sqrt{11}-3 \sqrt{2})^2}+\frac{11}{\sqrt{11}}.$ $2. B=\sqrt{(5-3 \sqrt{2})^2}+\sqrt{(\sqrt{11}-3 \sqrt{2})^2}+\frac{11}{\sqrt{11}}.$

Câu 2. (1 điểm) Rút gọn các biểu thức sau: $A=\frac{u-v}{\sqrt{u}+\sqrt{v}}-\frac{\sqrt{u^3}+\sqrt{v^3}}{u-v}$ $A=\frac{u-v}{\sqrt{u}+\sqrt{v}}-\frac{\sqrt{u^3}+\sqrt{v^3}}{u-v}$ với $u \geq 0, v \geq 0, u \neq v.$ $u \geq 0, v \geq 0, u \neq v.$

Câu 3. (3 điểm) Tìm x, biết:

$1. (2 \sqrt{x}+3)(2 \sqrt{x}-1)-\sqrt{x}(-3+4 \sqrt{x}).$ $1. (2 \sqrt{x}+3)(2 \sqrt{x}-1)-\sqrt{x}(-3+4 \sqrt{x}).$

$2. \frac{1}{5} \sqrt{25 x+50}-5 \sqrt{x+2}+\sqrt{9 x+18}+9=0.$ $2. \frac{1}{5} \sqrt{25 x+50}-5 \sqrt{x+2}+\sqrt{9 x+18}+9=0.$

$3. \sqrt{4 x^2-4 x+4}=7 x-1.$ $3. \sqrt{4 x^2-4 x+4}=7 x-1.$

Câu 4. (3,5 điểm)

1. Cho hình thang ABCD biết $A=90^{\circ} ; D=90^{\circ}$ $A=90^{\circ} ; D=90^{\circ}$ và A B<D C. Hai đường chéo A C và B D vuông góc với nhau tại O

a) Cho $A B=9 \mathrm{~cm}$ $A B=9 \mathrm{~cm}$ và $A=12 \mathrm{~cm}$ $A=12 \mathrm{~cm}$. Hãy

- Tính tỉ số lượng giác của các góc nhọn và cạnh BD của tam giác ADB.

- Tính độ dài các đoạn thẳng AO, DO và AC.

- Kẻ BH vuông góc với DC tại H. Tính diện tích tam giác DOH.

b) Chứng minh $BH^2=AB\cdot CD.$ $BH^2=AB\cdot CD.$

2. Tính $Q=\sin^210^{\circ}+\sin^220^{\circ}+\sin^230^{\circ}+\ldots+\sin^270^{\circ}+\sin^280^{\circ}.$ $Q=\sin^210^{\circ}+\sin^220^{\circ}+\sin^230^{\circ}+\ldots+\sin^270^{\circ}+\sin^280^{\circ}.$

Câu 5. (0,5 điểm) Cho 2016<x<2017. Tìm giá trị nhỏ nhất của

$S=\frac{1}{(x-2016)^2}+\frac{1}{(2017-x)^2}+\frac{1}{(x-2016)(2017-x)} .$ $S=\frac{1}{(x-2016)^2}+\frac{1}{(2017-x)^2}+\frac{1}{(x-2016)(2017-x)} .$

..................

Mời các bạn tải File về để xem thêm nội dung chi tiết tài liệu

Chia sẻ bởi: