Tam giác vuông: Khái niệm, tính chất, cách chứng minh và bài tập Diện tích tam giác vuông

Tam giác vuông là tài liệu vô cùng hữu ích mà Download.vn muốn giới thiệu đến quý thầy cô cùng các em học sinh lớp 7 tham khảo.

Tam giác vuông là tam giác có một góc vuông (góc 90 ⁰). Vậy công thức tính diện tích tam giác vuông như thế nào? Dấu hiệu nhận biết tam giác vuông. Tính chất tam giác vuông là gì? Cách chứng minh tam giác vuông ra sao? Mời các bạn hãy cùng chúng tôi theo dõi bài viết dưới đây nhé. Ngoài ra các bạn xem thêm kiến thức về tam giác cân.

1. Tam giác vuông là gì?

Tam giác vuông là tam giác có một góc vuông ( góc 90⁰)

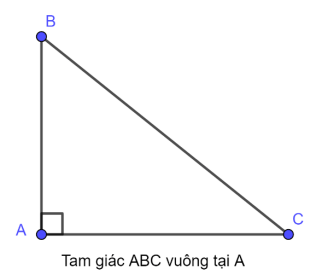
Tam giác ABC vuông tại A:

Cạnh BC đối diện với góc vuông gọi là cạnh huyền.

Hai cạnh AB và AC kề với góc vuông gọi là cạnh bên ( hay còn gọi là cạnh góc vuông)

2. Định lý Pytago

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

3. Dấu hiệu nhận biết tam giác vuông

• Tam giác có một góc vuông là tam giác vuông
• Tam giác có hai góc nhọn phụ nhau là tam giác vuông
• Tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia là tam giác vuông
• Tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy là tam giác vuông
• Tam giác nội tiếp đường tròn có một cạnh là đường kính của đường tròn là tam giác vuông

4. Diện tích tam giác vuông

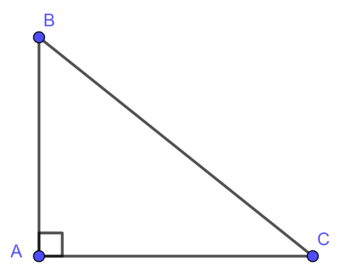
Trong tam giác vuông, nếu coi một cạnh góc vuông là đáy thì cạnh góc vuông còn lại là chiều cao. Diện tích tam giác bằng chiều dài đáy nhân với chiều cao tương ứng rồi chia 2.

Tam giác ABC vuông tại A

Diện tích tam giác ABC là:

\(S\ =\frac{AC.\ AB}{2}\)

Hoặc

\(S=\ \frac{a.b}{2}\)

Trong đó:

• S là diện tích tam giác
• a, b là độ dài 2 cạnh góc vuông

Giả sử có tam giác vuông ABC vuông tại A như hình sau:

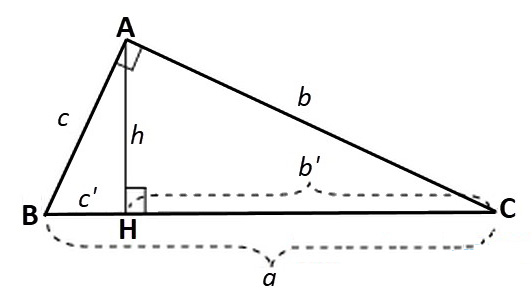
Công thức tính cạnh và đường cao trong tam giác vuông:

\(1.\ {a^2} = {b^2} + {c^2}\)

\(2.\ {b^2} = a.b' và {c^2} = a.c'\)

\(3.\ ah = bc\)

\(4.\ {h^2} = b'.c'\)

\(5.\ \frac{1}{{{h^2}}} = \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}\)

Trong đó: a, b, c lần lượt là các cạnh của tam giác vuông như hình trên;

b’ là đường chiếu của cạnh b trên cạnh huyền; c’ là đường chiếu của cạnh c trên cạnh huyền;

h là chiều cao của tam giác vuông được kẻ từ đỉnh góc vuông A xuống cạnh huyền BC.

Như vậy các bạn có thể dựa vào các công thức cạnh và đường cao trong tam giác vuông ở trên để giải quyết các bài toán.