Tổng hợp 250 câu hỏi trắc nghiệm vận dụng cao môn Toán (Có đáp án) Ôn thi THPT Quốc gia môn Toán

Tải về Bình luận

Tổng hợp 250 câu hỏi trắc nghiệm vận dụng cao môn Toán là tài liệu vô cùng hữu ích dành cho các bạn học sinh lớp 12 ôn tập thi THPT Quốc gia 2023.

Trắc nghiệm vận dụng cao môn Toán bao gồm 199 trang tuyển chọn 250 bài toán trắc nghiệm thuộc mức độ vận dụng bậc cao có đáp án và lời giải chi tiết, tài liệu được biên soạn bởi các thầy, cô trong nhóm Toán. Các bài toán được phân tích và giải tỉ mỉ để giúp các em học sinh dễ dạng tiếp thu được các bài toán ở mức độ khó. Vậy sau đây là trọn bộ tài liệu mời các bạn cùng đón đọc. Bên cạnh đó các bạn xem thêm 1287 bài tập trắc nghiệm nguyên hàm, tích phân và ứng dụng.

Tổng hợp 250 câu hỏi trắc nghiệm vận dụng cao môn Toán

Câu 1.1. Đường thẳng đi qua 2 điểm cực trị của đồ thị hàm số $y=\frac{x^2-2 x+3}{x-1}$ $y=\frac{x^2-2 x+3}{x-1}$ hợp với 2 trục tọa độ 1 tam giác có diện tích S bằng :

$A. \mathrm{S}=1,5$ $A. \mathrm{S}=1,5$

B. S=2

$C. \mathrm{CS}=3$ $C. \mathrm{CS}=3$

D. S=1

Câu 1.2. Khối cà̀u nội tiếp hình tứ diện đều có cạnh bằng a thì thể tích khối cà̀u là :

$A. \frac{a^3 \pi \sqrt{6}}{216}$ $A. \frac{a^3 \pi \sqrt{6}}{216}$

$B. \frac{a^3 \pi \sqrt{6}}{124}$ $B. \frac{a^3 \pi \sqrt{6}}{124}$

$C. \frac{a^3 \pi \sqrt{3}}{96}$ $C. \frac{a^3 \pi \sqrt{3}}{96}$

$D. \frac{a^3 \pi \sqrt{3}}{144}$ $D. \frac{a^3 \pi \sqrt{3}}{144}$

Câu 1.3. Tìm m để phương trình $e^{2 x}-m e^x+3-m=0$ $e^{2 x}-m e^x+3-m=0$ có nghiệm

$A. m \geq 2$ $A. m \geq 2$

B. m>2

C. m<3

D. m>0

Câu 1.4. Giá trị của tham số m để diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=3 x^2+2 m x+m^2+1$, trục hoành, trục tung và đường thẳng $\mathrm{x}=2$ $\mathrm{x}=2$ đạt giá trị nhỏ nhất là:

A. m=2

B. m=1

C. m=-1

D. m=-2

Câu 1.5. Phương trình nào sau đây không phải là phương trình hình chiếu vuông góc của đường thẳng $\mathrm{d}:\left\{\begin{array}{l}x=1+2 t \\ y=-2+3 t, t \in R \\ z=3+t\end{array}\right.$ $\mathrm{d}:\left\{\begin{array}{l}x=1+2 t \\ y=-2+3 t, t \in R \\ z=3+t\end{array}\right.$ trên mặt phẳng (Oxy) :

$A. \left\{\begin{array}{l}x=3+2 t^{\prime} \\ y=1+3 t^{\prime \prime}, t^{\prime} \in R \\ z=0\end{array}\right.$ $A. \left\{\begin{array}{l}x=3+2 t^{\prime} \\ y=1+3 t^{\prime \prime}, t^{\prime} \in R \\ z=0\end{array}\right.$

$B. \left\{\begin{array}{l}x=1+4 t^{\prime} \\ y=-2+6 t^{\prime}, t^{\prime} \in R \\ z=0\end{array}\right.$ $B. \left\{\begin{array}{l}x=1+4 t^{\prime} \\ y=-2+6 t^{\prime}, t^{\prime} \in R \\ z=0\end{array}\right.$

$C. \left\{\begin{array}{l}x=1+2 t^{\prime} \\ y=2+3 t^{\prime}, t^{\prime} \in R \\ z=0\end{array}\right.$ $C. \left\{\begin{array}{l}x=1+2 t^{\prime} \\ y=2+3 t^{\prime}, t^{\prime} \in R \\ z=0\end{array}\right.$

$d. \left\{\begin{array}{l}x=5-2 t^{\prime} \\ y=4-3 t^{\prime}, t^{\prime} \in R \\ z=0\end{array}\right.$ $d. \left\{\begin{array}{l}x=5-2 t^{\prime} \\ y=4-3 t^{\prime}, t^{\prime} \in R \\ z=0\end{array}\right.$

Câu 1.6. Gọi A, B, C lần lượt là các điểm biểu diễn của 3 số phức :

$1+2 \mathrm{i} ;(1-i)(1+2 i) ; \frac{2+6 i}{3-i}.$ $1+2 \mathrm{i} ;(1-i)(1+2 i) ; \frac{2+6 i}{3-i}.$ Diện tích của tam giác ABC bằng :

$A. \frac{1}{4}$ $A. \frac{1}{4}$

$B. \frac{1}{2}$ $B. \frac{1}{2}$

$C. \frac{\sqrt{5}}{5}$ $C. \frac{\sqrt{5}}{5}$

$D. \frac{\sqrt{5}}{2}$ $D. \frac{\sqrt{5}}{2}$

Câu 2.1. Cho hàm số $y=x^3-2 x^2+(1-m) x+m$ có đồ thị (C). Giá trị của m thì (C) cắt trục hoành tại 3 điểm phân biệt $x_1, x_2, x_3$ sao cho $x_1^2+x_2^2+x_3^2<4$ là

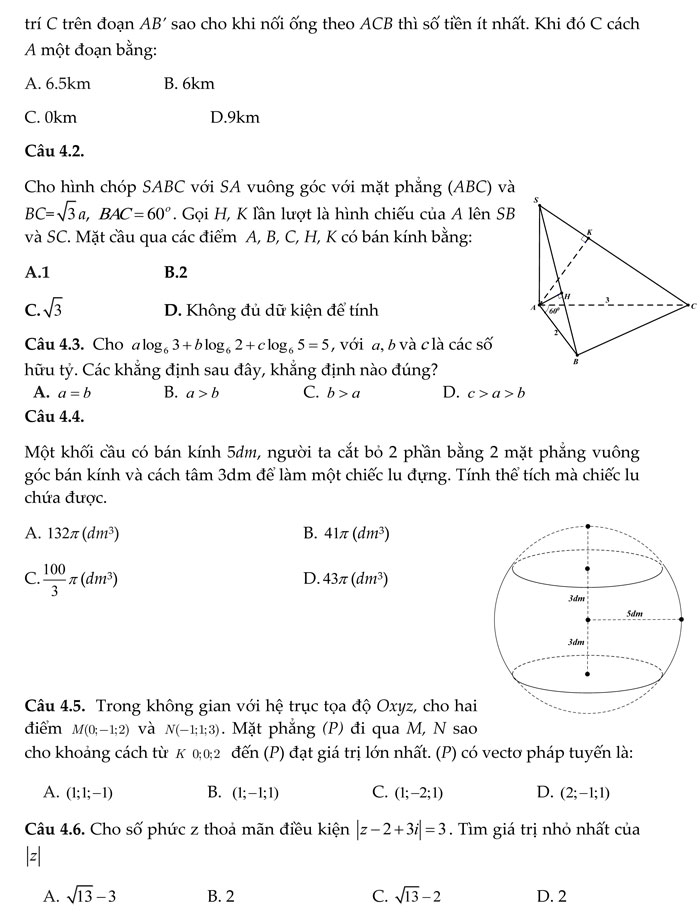
250 câu hỏi trắc nghiệm vận dụng cao môn Toán