Download.vn Học tập Lớp 9 Toán 9 Thi vào 10

Đề thi tuyển sinh lớp 10 THPT chuyên tỉnh Khánh Hòa năm 2012 - 2013 môn Toán Đề thi môn Toán

Tải về Bình luận
  • 1

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KHÁNH HÒA

ĐỀ THI CHÍNH THỨC

KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
NĂM HỌC 2012 - 2013

MÔN THI: TOÁN CHUYÊN
Ngày thi: 22/6/2012
Thời gian làm bài: 150 phút (không kể thời gian giao đề)

Bài 1. (2.00 điểm)

1) Rút gọn biểu thức 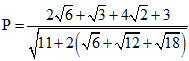Đề thi tuyển sinh lớp 10 THPT chuyên tỉnh Khánh Hòa năm 2012 - 2013 môn Toán.

2) Với n là số nguyên dương, cho các biểu thức Đề thi tuyển sinh lớp 10 THPT chuyên tỉnh Khánh Hòa năm 2012 - 2013 môn Toán và
Đề thi tuyển sinh lớp 10 THPT chuyên tỉnh Khánh Hòa năm 2012 - 2013 môn Toán

Tính tỉ số A/B.

Bài 2. (2.00 điểm)

1) Giải phương trình Đề thi tuyển sinh lớp 10 THPT chuyên tỉnh Khánh Hòa năm 2012 - 2013 môn Toán.

2) Giải hệ phương trình 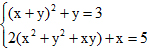Đề thi tuyển sinh lớp 10 THPT chuyên tỉnh Khánh Hòa năm 2012 - 2013 môn Toán.

Bài 3. (2.00 điểm)

1) Cho ba số a, b, c thỏa mãn và a3 > 36 và abc = 1. Chứng minh: a2 + 3(b2 + c2) > 3(ab + bc + ca).

2) Cho a thuộc Z và a ≥ 0. Tìm số phần tử của tập hợp 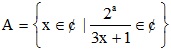Đề thi tuyển sinh lớp 10 THPT chuyên tỉnh Khánh Hòa năm 2012 - 2013 môn Toán(¢ là tập hợp các số nguyên).

Bài 4. (3.00 điểm)

Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O; R). Tiếp tuyến tại A của (O; R) cắt đường thẳng BC tại điểm M. Gọi H là chân đường cao hạ từ A xuống BC.

1) Chứng minh AB.AC = 2R.AH.

2) Chứng minh Đề thi tuyển sinh lớp 10 THPT chuyên tỉnh Khánh Hòa năm 2012 - 2013 môn Toán.

3) Trên cạnh BC lấy điểm N tùy ý (N khác B và C). Gọi E, F lần lượt là hình chiếu vuông góc của N lên AB, AC. Tìm vị trí của N để độ dài đoạn EF nhỏ nhất.

Bài 5. (1.00 điểm)

Cho tam giác ABC có đường cao AH, biết H thuộc cạnh BC và BH = BC/3. Trên tia đối của tia HA, lấy điểm K sao cho: Đề thi tuyển sinh lớp 10 THPT chuyên tỉnh Khánh Hòa năm 2012 - 2013 môn Toán. Chứng minh: AK.BC = AB.KC + AC.BK.

Download tài liệu để xem thêm chi tiết.

Chia sẻ bởi:
Liên kết tải về
Tìm thêm: Toán 9

Nhiều người đang xem

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨

Tài liệu tham khảo khác

Chủ đề liên quan

KHO TÀI LIỆU GIÁO DỤC & HỖ TRỢ CAO CẤP

Mở khóa quyền truy cập vào hàng ngàn tài liệu độc quyền và nhận hỗ trợ nhanh chóng từ đội ngũ của chúng tôi.

Hỗ trợ tư vấn

Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu

Hotline

024 322 333 96

Có thể bạn quan tâm

Xem thêm

Mới nhất trong tuần

Đóng
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ
Nhắn tin Zalo