Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn (không bao gồm tài liệu cao cấp) và trải nghiệm website không quảng cáo
Tìm hiểu thêm »170 bài toán luyện thi học sinh giỏi lớp 5 là tài liệu tham khảo và ôn tập hay dành cho quý thầy cô giáo và các em học sinh. Thông qua tài liệu này sẽ giúp các em học sinh ôn tập, củng cố kiến thức của môn Toán. Hi vọng rằng tài liệu này sẽ giúp các em nắm vững những kiến thức, các dạng bài tập của môn Toán để tự tin bước vào kỳ thi học sinh giỏi Toán lớp 5 đạt kết quả cao. Sau đây, mời các em cùng tham khảo tài liệu.
Bài 1: Số có 1995 chữ số 7 khi chia cho 15 thì phần thập phân của thương là bao nhiêu?
Giải: Gọi số có 1995 chữ số 7 là A. Ta có:
Một số chia hết cho 3 khi tổng các chữ số của số đó chia hết cho 3. Tổng các chữ số của A là 1995 x 7. Vì 1995 chia hết cho 3 nên 1995 x 7 chia hết cho 3. Do đó A = 777…77777 chia hết cho 3.
1995 chữ số 7
Một số hoặc chia hết cho 3 hoặc chia cho 3 cho số dư là 1 hoặc 2.
Chữ số tận cùng của A là 7 không chia hết cho 3, nhưng A chia hết cho 3 nên trong phép chia của A cho 3 thì số cuối cùng chia cho 3 phải là 27. Vậy chữ số tận cùng của thương trong phép chia A cho 3 là 9, mà 9 x 2 = 18, do đó số A/3 x 0,2 là số có phần thập phân là 8.
Vì vậy khi chia A = 777…77777 cho 15 sẽ được thương có phần thập phân là 8.
1995 chữ số 7
Nhận xét : Điều mấu chốt trong lời giải bài toán trên là việc biến đổi A/15 = A/3 x 0,2 Sau đó là chứng minh A chia hết cho 3 và tìm chữ số tận cùng của thương trong phép chia A cho 3. Ta có thể mở rộng bài toán trên tới bài toán sau :
Bài 2 (1*): Tìm phần thập phân của thương trong phép chia số A cho 15 biết rằng số A gồm n chữ số a và A chia hết cho 3?
Giải:
Nếu kí hiệu A = aaa…aaaa và giả thiết A chia hết cho 3 (tức là n x a chia hết cho 3), thì khi n chữ số a đó tương tự như cách giải bài toán 1 ta tìm được phần thập phân của thương khi chia A cho 15 như sau:
– Với a = 1 thì phần thập phân là 4 (A = 111…1111 , với n chia hết cho 3) n chữ số 1
– Với a = 2 thì phần thập phân là 8 (A = 222…2222 , với n chia hết cho 3) n chữ số 2
– Với a = 3 thì phần thập phân là 2 (A = 333…3333 , với n tùy ý) n chữ số 3
– Với a = 4 thì phần thập phân là 6 (A = 444…4444 , với n chia hết cho 3) n chữ số 4
– Với a = 5 thì phần thập phân là 0 (A = 555…5555 , với n chia hết cho 3) n chữ số 5
– Với a = 6 thì phần thập phân là 4 (A = 666…6666 , với n tùy ý) n chữ số 6
– Với a = 7 thì phần thập phân là 8 (A = 777…7777 , với n chia hết cho 3) n chữ số 7
– Với a = 8 thì phần thập phân là 2 (A = 888…8888 , với n chia hết cho 3) n chữ số 8
– Với a = 9 thì phần thập phân là 6 (A = 999…9999 , với n tùy ý) n chữ số 9
Trong các bài toán 1 và 2 (1*) ở trên thì số chia đều là 15. Bây giờ ta xét tiếp một ví dụ mà số chia không phải là 15.
Bài 3. Tìm phần thập phân của thương trong phép chia số 111…1111 cho 36? 2007 chữ số 1
Giải: Đặt A = 111…1111
2007 chữ số 1
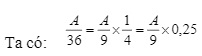
Vì 0,25 có hai chữ số ở phần thập phân nên ta sẽ tìm hai chữ số tận cùng của thương trong phép chia A cho 9.
Một số chia hết cho 9 khi tổng các chữ số của số đó chia hết cho 9. Tổng các chữ số của A là 2007 x 1 = 2007. Vì 2007 chia hết cho 9 nên A = 111….1111 chia hết cho 9.
2007 chữ số 1
Một số hoặc chia hết cho 9 hoặc chia cho 9 cho số dư là một trong các số 1, 2, 3, 4, 5, 6, 7, 8. Chữ số tận cùng của A là 1 không chia hết cho 9, nhưng A chia hết cho 9 nên trong phép chia của A cho 9, thì ở bước cuối (ta gọi là bước k) : số chia cho 9 phải là 81. Vậy chữ số tận cùng của thương trong phép chia A cho 9 là 9. Cũng trong phép chia của A cho 9, ở trước bước cuối (bước k – 1) : số chia cho 9 cho số dư là 8 sẽ là 71 và khi đó ở thương ta được số giáp số cuối cùng là 7.
Vậy hai chữ số tận cùng của thương trong phép chia A cho 9 là 79.
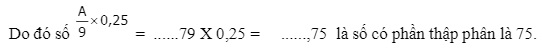
Nhận xét:
a) Vì số 0,25 có phần thập phân là số có hai chữ số, nên nếu ta chỉ tìm một chữ số tận cùng của thương trong phép chia A cho 9 và sau đó nhân chữ số cuối này với 0,25 thì kết quả sẽ không đúng.
b) Cũng có thể biến đổi 36 = 12 x 3 hoặc 36 = 6 x 6, … tuy nhiên việc tính toán sẽ phức tạp và trong nhiều trường hợp là không thực hiện được.
Vận dụng: Tìm phần thập phân trong thương của phép chia:
a) Số 111…1111 chia cho 12 ?
2001 chia là 1
b) Số 888…8888 chia cho 45 ?
2007 chia là 1
c) Số 333..3333 chia cho 24 ?
1000000 chia là 3
Bài 4: Cho mảnh bìa hình vuông ABCD. Hãy cắt từ mảnh bìa đó một hình vuông sao cho diện tích còn lại bằng diện tích của mảnh bìa đã cho.
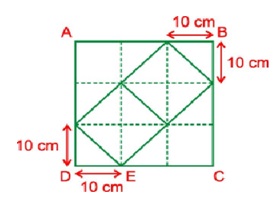
Bài giải:
Theo đầu bài thì hình vuông ABCD được ghép bởi 2 hình vuông nhỏ và 4 tam giác (trong đó có 2 tam giác to, 2 tam giác con). Ta thấy có thể ghép 4 tam giác con để được tam giác to đồng thời cũng ghép 4 tam giác con để được 1 hình vuông nhỏ. Vậy diện tích của hình vuông ABCD chính là diện tích của 2 + 2 x 4 + 2 x 4 = 18 (tam giác con). Do đó diện tích của hình vuông ABCD là: 18 x (10 x 10) / 2 = 900 (cm2)
Tài liệu vẫn còn, mời các bạn tải về để xem tiếp
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: