Tổng hợp kiến thức cơ bản môn Toán lớp 6 Tóm tắt kiến thức lớp 6 môn Toán

Tổng hợp kiến thức cơ bản môn Toán lớp 6 giúp các em học sinh nắm chắc toàn bộ kiến thức cơ bản trong chương trình môn Toán 6, để ôn tập thật tốt, dễ dàng đạt kết quả cao trong các bài kiểm tra, bài thi của mình.

Với kiến thức Toán lớp 6 cả phần Số học và Hình học, các em sẽ nắm vững những kiến thức trọng tâm nhất của môn Toán lớp 6 như: Số tự nhiên, Số nguyên, Phân số, Đoạn thẳng, Góc,.... Mời các em cùng theo dõi bài viết dưới đây của Download.vn:

Tổng hợp kiến thức cơ bản môn Toán lớp 6 sách mới

Trọn bộ kiến thức môn Toán sách mới, các em học sinh cùng tham khảo chi tiết sau đây:

• Toán lớp 6 sách Kết nối tri thức với cuộc sống
• Toán lớp 6 sách Chân trời sáng tạo
• Toán lớp 6 sách Cánh Diều

Tổng hợp kiến thức cơ bản môn Toán lớp 6 sách cũ

Tài liệu bao gồm toàn bộ 18 trang, tóm tắt toàn bộ kiến thức toán lớp 6 cả phần Số học và Hình học. Phần Số học gồm 3 chương:

• Chương I: Ôn tập và bổ túc về số tự nhiên
• Chương II: Số nguyên
• Chương III: Phân số

Còn phần Hình học gồm 2 chương:

• Chương I: Đoạn thẳng
• Chương II. Góc.

Qua đó, giúp các bạn học sinh lớp 6 ôn tập và củng cố kiến thức được tốt nhất. Sau đây là nội dung chi tiết, mời các bạn cùng tham khảo và tải tài liệu tại đây.

CHƯƠNG I: ÔN TẬP VÀ BỔ TÚC VỀ SỐ TỰ NHIÊN

1. Tập hợp. Phần tử của tập hợp:

- Tập hợp là một khái niệm cơ bản. Ta hiểu tập hợp thông qua các ví dụ.

- Tên tập hợp được đặt bằng chữ cái in hoa.

- Các phần tử của một tập hợp được viết trong hai dấu ngoặc nhọn { }, cách nhau bởi dấu ";" (nếu có phần tử là số) hoặc dấu ",". Mỗi phần tử được liệt kê một lần, thứ tự liệt kê tùy
ý.

- Kí hiệu: 1 \(\in\) A đọc là 1 thuộc A hoặc 1 là phần tử của A;
                5 \(\notin\) A đọc là 5 không thuộc A hoặc 5 không là phần tử của A;

- Để viết một tập hợp, thường có hai cách:

• Liệt kê các phần tử của tập hợp.
• Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp đó.

- Một tập hợp có thể có một phần tử, có nhiều phần tử, có vô số phần tử, cũng có thể không có phần tử nào (tức tập hợp rỗng, kí hiệu \(\varnothing\) .

- Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A gọi là tập hợp con của tập hợp B. Kí hiệu: A ⊂ B đọc là: A là tập hợp con của tập hợp B hoặc A được chứa trong B hoặc B chứa A.

- Mỗi tập hợp đều là tập hợp con của chính nó. Quy ước: tập hợp rỗng là tập hợp con của mọi tập hợp.

* Cách tìm số tập hợp con của một tập hợp: Nếu A có n phần tử thì số tập hợp con của tập hợp A là 2ⁿ.

- Giao của hai tập hợp (kí hiệu: ∩) là một tập hợp gồm các phần tử chung của hai tập hợp đó.

2. Tập hợp các số tự nhiên: Kí hiệu N

- Mỗi số tự nhiên được biểu diễn bởi một điểm trên tia số. Điểm biểu diễn số tự nhiên a trên tia số gọi là điểm a.

- Tập hợp các số tự nhiên khác 0 được kí hiệu là N*

- Thứ tự trong tập hợp số tự nhiên:

• Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia. Trên hai điểm trên tia số, điểm ở bên trái biểu diễn số nhỏ hơn.
• Nếu a < b và b < c thì a < c.
• Mỗi số tự nhiên có một số liền sau duy nhất, chẳng hạn số tự nhiên liền sau số 2 là số 3; số liền trước số 3 là số 2; số 2 và số 3 là hai số tự nhiên liên tiếp. Hai số tự nhiên liên tiếp thì hơn kém nhau một đơn vị.
• Số 0 là số tự nhiên nhỏ nhất. Không có số tự nhiên lớn nhất.
• Tập hợp các số tự nhiên có vô số phần tử.

3. Ghi số tự nhiên: Có nhiều cách ghi số khác nhau:

- Cách ghi số trong hệ thập phân: Để ghi các số tự nhiên ta dùng 10 chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Cứ 10 đơn vị ở một hàng thì làm thành một đơn vị ở hàng liền trước nó.

+ Kí hiệu: \(\overline{ab}\) chỉ số tự nhiên có hai chữ số, chữ số hàng chục là a, chữ số hàng đơn vị là b. Viết được \(\overline{ab}\) = a.10 + b

\(\overline{abc}\) chỉ số tự nhiên có ba chữ số, chữ số hàng trăm là a, chữ số hàng chục là b, chữ số hàng đơn vị là c. Viết được \(\overline{abc}\) = a.100 + b.10 + c

- Cách ghi số La Mã: có 7 chữ số

• Mỗi chữ số La Mã không viết liền nhau quá ba lần.
• Chữ số có giá trị nhỏ đứng trước chữ số có giá trị lớn làm giảm giá trị của chữ số có giá
  trị lớn.

- Cách ghi số trong hệ nhị phân: để ghi các số tự nhiên ta dùng 2 chữ số là : 0 và 1

- Các ví dụ tách một số thành một tổng:

Trong hệ thập phân: 6478 = 6. 10³ + 4. 10² + 7. 10¹ + 8. 10⁰

Trong hệ nhị phân: 1101 = 1. 2³ + 1. 2² + 0. 2¹ + 1. 2⁰

4. Các phép toán:

Tổng quát: Cho hai số tự nhiên a và b, trong đó b ≠ 0, ta luôn tìm được hai số tự nhiên q và r duy nhất sao cho:

a        =      b        .        q      +      r            trong đó 0 ≤ r < b
(số bị chia) = (số chia) . (thương) + (số dư)

• Nếu r = 0 thì ta có phép chia hết.
• Nếu r ≠ 0 thì ta có phép chia có dư.

* Tính chất của phép cộng và phép nhân số tự nhiên:

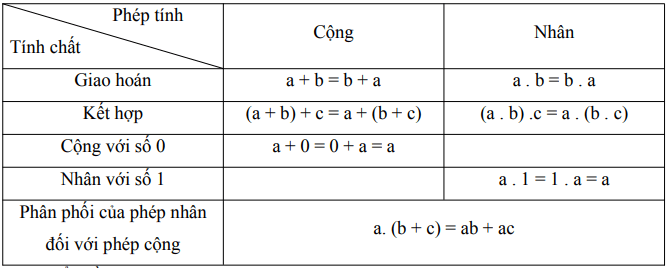
Phát biểu bằng lời:

Tính chất giao hoán:

• Khi đổi chỗ các số hạng trong một tổng thì tổng không thay đổi.
• Khi đổi chỗ các thừa số trong một tích thì tích không đổi.

Tính chất kết hợp:

• Muốn cộng một tổng hai số với một số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ hai và số thứ ba.
• Muốn nhân một tích hai số với một số thứ ba, ta có thể nhân số thứ nhất với tích của số thứ hai và số thứ ba.

Tính chất phân phối của phép nhân đối với phép cộng:

Muốn nhân một số với một tổng, ta có thể nhân số đó với từng số hạng của tổng, rồi cộng các kết quả lại.

e, Chú ý:

• Trong tính toán có thể thực hiện tương tự với tính chất a(b - c) = ab - ac
• Dạng tổng quát của số chẵn (số chia hết cho 2) là 2k (k \(\in\) N), dạng tổng quát của số lẻ (số chia cho 2 dư 1) là 2k + 1 (k \(\in\) N).

f, Phép nâng lên lũy thừa:

- ĐN: Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a.

\(\mathrm{a}^{\mathrm{n}}=\underbrace{\mathrm{a} \cdot \mathrm{a} \ldots \ldots \mathrm{a}}_{\mathrm{n} \text { thừa số }}(\mathrm{n} \neq 0)\) a gọi là cơ số, n gọi là số mũ.

a² gọi là a bình phương (hay bình phương của a);
a³ gọi là a lập phương (hay lập phương của a)

Quy ước: a¹ = a          ; a⁰ = 1 (a≠ 0)

- Nhân hai lũy thừa cùng cơ số: Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ.

a^m . aⁿ = a^m+n

- Chia hai lũy thừa cùng cơ số: Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ.

a^m : aⁿ = a^m-n (với a≠ 0; m ≥ n )

- Thêm: (a^m)ⁿ = a^m.n             ; (a.b)ⁿ = aⁿ . bⁿ

* Số chính phương: là số bằng bình phương của một số tự nhiên (VD: 0, 1, 4, 9, ...)

5. Thứ tự thực hiện các phép tính:

- Đối với biểu thức không có dấu ngoặc:

• Nếu chỉ có phép cộng, trừ hoặc chỉ có phép nhân, chia, ta thực hiện phép tính theo thứ tự từ trái sang phải.
• Nếu có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa, ta thực hiện theo thứ tự: Lũy thừa → Nhân và chia → Cộng và trừ.

- Đối với biểu thức có dấu ngoặc ta thực hiện theo thứ tự ( ) → [ ] → { }

6. Tính chất chia hết của một tổng:

- Tính chất 1: Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.

a \(\vdots\) m, b \(\vdots\) m, c \(\vdots\) m ⇒ (a + b + c) \(\vdots\) m

- Tính chất 2: Nếu chỉ có một số hạng của tổng không chia hết cho một số, còn các số hạng khác đều chia hết cho số đó thì tổng không chia hết cho số đó.

a  m, b \(\vdots\) m, c \(\vdots\) m ⇒ (a + b + c) m

7. Dấu hiệu chia hết cho 2, 3, 5, 9:

8. Ước và bội:

- Nếu có số tự nhiên a chia hết cho số tự nhiên b thì ta nói a là bội của b, còn b là ước của a.

- Ta có thể tìm các bội của một số bằng cách nhân số đó lần lượt với 0, 1, 2, 3,...

- Ta có thể tìm các ước của a bằng cách lần lượt chia a cho các số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a

- Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có 2 ước là 1 và chính nó. Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn 2 ước.

* Cách kiểm tra 1 số là số nguyên tố: Để kết luận số a là số nguyên tố (a>1), chỉ cần chứng tỏ rằng nó không chia hết cho mọi số nguyên tố mà bình phương không vượt quá a.

- Phân tích một số tự nhiên lớn hơn 1 ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố

* Cách tính số lượng các ước của một số m (m > 1): ta xét dạng phân tích của số m ra thừa số nguyên tố:

• Nếu m = a^x thì m có x + 1 ước
• Nếu m = a^x . b^y thì m có (x + 1)(y + 1) ước
• Nếu m = a^x . b^y . c^z thì m có (x + 1)(y + 1)(z + 1) ước.

- Ước chung của hai hay nhiều số là ước của tất cả các số đó.

- Bội chung của hai hay nhiều số là bội của tất cả các số đó.

- ƯCLN của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.

- Các số nguyên tố cùng nhau là các số có ƯCLN bằng 1

- Để tìm ước chung của các số đã cho, ta có thể tìm các ước của ƯCLN của các số đó.

- BCNN của hai hay nhiều số là số lớn nhất khác 0 trong tập hợp các bội chung của các số đó.

- Để tìm BC của các số đã cho, ta có thể tìm các bội của BCNN của các số đó.

- Cách tìm ƯCLN và BCNN:

* Bổ sung:

• Tích của hai số tự nhiên khác 0 bằng tích của ƯCLN và BCNN của chúng: a . b = ƯCLN(a,b). BCNN(a,b)
• Nếu tích a.b chia hết cho m, trong đó b và m là hai số nguyên tố cùng nhau thì a \(\vdots\)  m
• Một cách khác tìm ƯCLN của hai số a và b (với a > b): Chia số lớn cho số nhỏ.

CHƯƠNG II: SỐ NGUYÊN

1. Tập hợp các số nguyên:

- Trong đời sống hàng ngày người ta dùng các số mang dấu "-" và dấu "+" để chỉ các đại lượng có thể xét theo hai chiều khác nhau.

- Tập hợp: {...; -3; -2; -1; 0; 1; 2; 3; ...} gồm các số nguyên âm, số 0 và các số nguyên dương là tập hợp các số nguyên. Kí hiệu là Z.

- Các số đối nhau là: 1 và -1; 2 và -2; a và -a;...

- So sánh hai số nguyên a và b: a < b => điểm a nằm bên trái điểm b trên trục số.

+ Mọi số nguyên dương đều lớn hơn số 0.

+ Mọi số nguyên âm đều nhỏ hơn số 0.

+ Mọi số nguyên âm đều nhỏ hơn bất kì số nguyên dương nào.

2. Giá trị tuyệt đối của số nguyên a, kí hiệu |a| là khoảng cách từ điểm a đến điểm gốc 0 trên trục số.

...............................................

Tài liệu vẫn còn, mời bạn tải về xem tiếp