™
Download.vn Học tập Thi vào 10

Đề thi tuyển sinh lớp 10 THPT tỉnh Long An năm học 2013 - 2014 môn Toán (Có đáp án) Sở GD-ĐT Long An

Tải về Bình luận
  • 1

SỞ GIÁO DỤC VÀ ĐÀO TẠO
LONG AN

ĐỀ THI CHÍNH THỨC

KỲ THI TUYỂN SINH VÀO LỚP 10 THPT
NĂM HỌC 2013 - 2014

MÔN THI: TOÁN (CÔNG LẬP)
Ngày thi: 26/06/2013
Thời gian làm bài: 120 phút (không kể thời gian giao đề)

Câu 1: (2 điểm)

1. Rút gọn các biểu thức sau: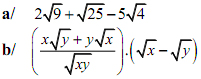
Đề thi tuyển sinh lớp 10 THPT tỉnh Long An năm học 2013 - 2014 môn Toán (Với x >0, y > 0)

2. Giải phương trình: Đề thi tuyển sinh lớp 10 THPT tỉnh Long An năm học 2013 - 2014 môn Toán

Câu 2: (2 điểm)

Cho các hàm số (P): y = 2x2 và (d): y = -x + 3

a/ Vẽ đồ thị của hai hàm số trên cùng mặt phẳng tọa độ Oxy.

b/ Tìm tọa độ giao điểm của hai đồ thị trên.

Câu 3: (2 điểm)

a/ Giải phương trình: 2x2 - 7x + 6 = 0

b/ Giải hệ phương trình: Đề thi tuyển sinh lớp 10 THPT tỉnh Long An năm học 2013 - 2014 môn Toán

c/ Cho phương trình ẩn x: x2 + 2mx + m2 - m + 1 = 0 (với m là tham số).

Tìm m để phương trình trên có nghiệm kép.Tính nghiệm kép đó với m vừa tìm được.

Câu 4: (4 điểm)

1. Cho tam giác ABC vuông tại A có AB = 3 cm, BC = 5 cm, AH là chiều cao của tam giác ABC. Tính độ dài AC và AH.

2. Cho tam giác nhọn ABC nội tiếp đường tròn (O;R). Ba đường cao AE, BF, CG cắt nhau tại H (với E thuộc BC, F thuộc AC, G
thuộc AB).

a/ Chứng minh các tứ giác AFHG và BGFC là các tứ giác nội tiếp.

b/ Gọi I và M lần lượt là tâm các đường tròn ngoại tiếp của các tứ giác AFHG và BGFC. Chứng minh MG là tiếp tuyến của đường tròn tâm I .

c/ Gọi D là giao điểm thứ hai của AE với đường tròn tâm O. Chứng minh: EA2 + EB2 + EC2 + ED2 = 4R2.

Download tài liệu để xem thêm chi tiết.

Chia sẻ bởi: 👨 Nguyễn Thu Ngân
Liên kết tải về
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨

Tài liệu tham khảo khác

Chủ đề liên quan

Có thể bạn quan tâm

Xem thêm

Mới nhất trong tuần

Đóng
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ
Chia sẻ
Chia sẻ FacebookChia sẻ Twitter
Đóng