Đề thi cao học trường Kinh tế Quốc Dân năm 2011 - Môn Toán kinh tế Đề thi cao học

Câu 1 (1 điểm): Cho mô hình cân bằng kinh tế:
Y = C + I₀ + G₀; C = C₀ + b(Y – T); T = T₀ + tY
Cho C₀ = 80; I₀ = 90; G₀ = 81; T₀ = 20; b = 0,9; t = 0,1.

a - Xác định mức cân bằng của Y.

b - Khi C0 tăng 1% thì mức cân bằng của Y tăng bao nhiêu %?

Câu 2 (2 điểm): Cho mẫu ngẫu nhiên W = (X1, X2, X3, X4, X5) từ tổng thể có phân phối chuẩn N(μ, σ²). Lập các thống kê:

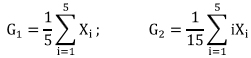
a - Nêu quy luật phân phối xác suất, tính kỳ vọng và phương sai của G1.

b - Nếu dùng hai thống kê trên để ước lượng cho μ thì thống kê nào tốt hơn? Tại sao?

Câu 3 (3 điểm): Một hộ gia đình có hàm lợi ích tiêu dùng với 2 loại hàng hoá là:
U(x₁, x₂) = 20x₁^0,45x₂^0,55, (x1 > 0, x2 > 0)
Trong đó x₁, x₂ tương ứng là số đơn vị của 2 loại hàng hoá, với giá p1 = 6, p2 = 11. Ngân sách tiêu dùng là B = 600.

a - Lập hàm Lagrange để tìm cực trị hàm lợi ích với ràng buộc ngân sách tiêu dùng.

b - Tìm gói hàng cực đại hàm lợi ích.

c - Khi ngân sách tiêu dùng tăng 1 đơn vị thì giá trị cực đại lợi ích tăng bao nhiêu đơn vị?

Câu 4 (1 điểm): Thu nhập/quý của công nhân xí nghiệp A là biến ngẫu nhiên phân phối chuẩn. Quan sát ngẫu nhiên thu nhập của 100 công nhân xí nghiệp A được số liệu sau:

Với mức ý nghĩa 5%, có thể cho rằng độ phân tán của thu nhập (tính bằng độ lệch chuẩn) nhỏ hơn 1,2 triệu hay không?

Câu 5 (2 điểm): Khảo sát trọng lượng X của một loại sản phẩm, quan sát một số sản phẩm được chọn ngẫu nhiên được số liệu sau:

Giả thiết trọng lượng của sản phẩm trên có phân phối chuẩn.

a - Ước lượng trọng lượng trung bình của loại sản phẩm trên với mức tin cậy 95%.

b - Nếu muốn độ dài khoảng tin cậu ở câu a không vượt quá 0,9 gam thì cần phải quan sát thêm ít nhất bao nhiêu sản phẩm?

c - Với mức ý nghĩa 5%, có thể cho rằng tỷ lệ sản phẩm có trọng lượng không quá 15 gam lớn hơn 15% hay không?

Câu 6 (1 điểm): Doanh nghiệp độc quyền có hàm nhu cầu Q = Q(p) với p > 0, Q’(p) < 0, trong đó Q là số sản phẩm và p là giá đơn vị sản phẩm. Chứng tỏ rằng nếu hệ số co giản của cầu theo giá: ε^Q_p > - 1 (tức là hàm cầu ít co giãn theo giá) thì doanh thu của doanh nghiệp sẽ tăng theo giá:

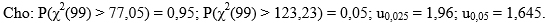
Download tài liệu để xem thêm chi tiết