Đề thi khảo sát chất lượng đầu năm môn Toán lớp 8 năm học 2016 - 2017 (Có đáp án) Đề kiểm tra chất lượng đầu năm môn Toán lớp 8

Download.vn xin gửi đến quý thầy cô giáo và các bạn học sinh đề thi khảo sát chất lượng đầu năm môn Toán lớp 8 năm học 2016 - 2017. Đây là đề kiểm tra chất lượng đầu năm lớp 8 nhằm đánh giá chất lượng học sinh. Đề thi khảo sát chất lượng đầu năm môn Toán lớp 8 có đáp án chi tiết kèm theo sẽ giúp các em học sinh ôn tập các dạng bài tập Toán chuẩn bị cho bài thi khảo sát chất lượng đầu năm.

Đề thi khảo sát chất lượng đầu năm môn Toán lớp 8

NĂM HỌC 2016 – 2017

Môn: Toán – Khối : 8

Thời gian làm bài: 90 phút (Không kể thời gian phát đề)

(Học sinh làm bài trên giấy thi. Cần ghi rõ họ tên, lớp, môn thi và mã đề vào tờ giấy làm bài.)

Câu1: (1 điểm)

a) Muốn nhân hai đơn thức ta làm như thế nào?

b) Áp dụng: Tính tích của 3x²yz và –5xy³

Câu 2: (1 điểm)

a) Nêu tính chất ba đường trung tuyến của tam giác.

b) Áp dụng: Cho ΔABC, AM là đường trung tuyến (MЄBC).

G là trọng tâm. Tính AG biết AM = 9cm.

Câu 3: (2,5 điểm)

a) Viết đa thức sau dưới dạng tích của hai đa thức: 4x² – 9y²

b) Rút gọn biểu thức: (x +3)² + (4 -x) (x +8)

c) Tính nhanh giá trị biểu thức: A = x² – 6x + 10 tại x = 103

Câu 4: (2,5 điểm)

Cho hai đa thức ∈

a. Sắp xếp các hạng tử của mỗi đa thức trên theo luỹ thừa giảm dần của biến.

b. Tính P(x) + Q(x) và P(x) – Q(x).

Câu 5: (3 điểm)

Cho ΔABC vuông tại A. Đường phân giác BD (DЄ AC). Kẻ DH vuông góc với BC (H ∈ BC). Gọi K là giao điểm của BA và HD.

Chứng minh:

a) AD=HD

b) BD⊥KC

c) ∠DKC= ∠DCK

—– HẾT —–

Đáp án đề thi khảo sát đầu năm môn Toán lớp 8

Câu 1.

a) Nêu đúng cách nhân hai đơn thức (0,5 điểm)

b) 3x²yz .( –5xy³)=-15x³y⁴z (0,5 điểm)

Câu 2.

a) Nêu đúng tính chất (0,5 điểm)

Câu 3.

a) Viết được dưới dạng tích: (2x – 3y)(2x + 3y) (1 điểm)

b) Tính được: (x +3)² = x² + 6x + 9 (0,5 điểm)

Tính được: (4 -x) (x + 8) = 4x + 3 – x² – 8x (0,25 điểm)

Thu gọn đến kết quả: 2x + 12 (0,25 điểm)

c) A = x²– 6x + 9 + 1 = (x -3)²+ 1

Thay số ta được giá trị A = 10001 (0,5 điểm)

Câu 4.

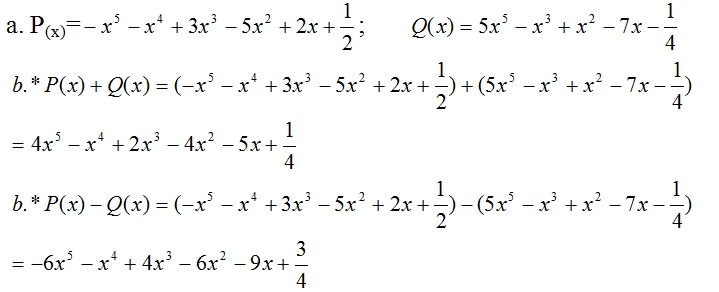
Câu 5.

Vẽ hình, giải thích, kết luận đúng (0,5 điểm)

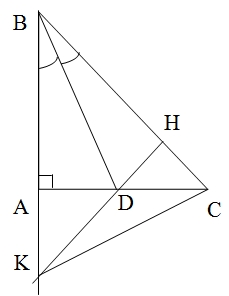
a) Chứng minh được

ΔABD= ΔHBD (cạnh huyền – góc nhọn).

=>AD=HD ( Cạnh tương ứng)

b) Xét ΔBKC có D là trực tâm => BD là đường cao ứng cạnh KC

=> BD vuông góc KC

c) ΔAKD= ΔHCD ( cạnh góc vuông- góc nhọn kề)

=>DK=DC =>ΔDKC cân tại D => DKC=DCK