Đề thi học sinh giỏi tỉnh Hà Tĩnh môn Toán lớp 9 năm học 2010 - 2011 Đề thi học sinh giỏi tỉnh

Bài 1. Cho phương trình:

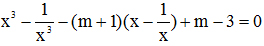
a) Giải phương trình khi m = 2.

b) Tìm m để phương trình có đúng hai nghiệm dương phân biệt.

Bài 2

a) Cho a, b, c là những số nguyên thỏa mãn điều kiện:

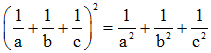
Chứng minh rằng a³ + b³ + c³ chia hết cho 3.

b) Giải phương trình: x³ + ax² + bx + 1 =0, biết rằng a, b là các số hữu tỉ và 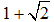là một nghiệm của phương trình.

Bài 3. Cho x, y là các số nguyên dương, thỏa mãn: x + y = 2011

Tìm giá trị lớn nhất và nhỏ nhất của biểu thức: P = x(x² + y) + y(y² + x)

Bài 4. Cho nửa đường tròn tâm O, đường kính AB = 2R, một dây cung MN = R di chuyển trên nửa đường tròn. Qua M kẻ đường thẳng song song với ON cắt đường thẳng AB tai E. Qua N kẻ đường thẳng song song với OM cắt đường thẵng AB tại F.

a) Chứng minh tam giác MNE và tam giác NFM đồng dạng .

b) Gọi K là giao điểm của EN và FM. Hãy xác định vị trí của dây MN để tam giác MKN có chu vi lớn nhất.

Bài 5. Cho a, b, c là những số dương thỏa mãn: abc = 1

Chứng minh: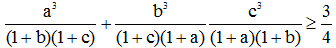

Download tài liệu để xem thêm chi tiết