Hỗ trợ tư vấn
Tư vấn - Giải đáp - Hỗ trợ đặt tài liệu
Mua gói Pro để tải file trên Download.vn (không bao gồm tài liệu cao cấp) và trải nghiệm website không quảng cáo
Tìm hiểu thêm »
SỞ GIÁO DỤC VÀ ĐÀO TẠO
|
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH
|
TỔNG QUAN ĐỀ THI
| STT | Tên bài | File chương trình |
| 1 | Bảng kết quả bóng đá | Bai1.* |
| 2 | Hình xoắn ốc | Bai2.* |
| 3 | Chọn đội tuyển Olympic | Bai3.* |
Dấu * được thay thế bởi PAS hoặc CPP của ngôn ngữ lập tr ình được sử dụng tương ứng là Pascal, Free Pascal hoặc C++.
Bài 1: (5 điểm) Bảng kết quả bóng đá
Bảng kết quả của 1 giải vô địch bóng đá được cho bởi ma trận vuông A(N,N): các phần tử ở đường chéo chính bằng 0, đội i thắng đội j thì A[i,j]=2, hoà thì A[i,j]=1, thua thì A[i,j]=0
a) Tìm các đội có số trận thắng lớn hơn số trận thua.
b) Tìm đội không thua trận nào.
c) Đội nào có nhiều điểm nhất.
Bài 2: (7 điểm) Hình xoắn ốc
Nhập số tự nhiên N, tạo bảng vuông NxN các số 1,2,3,....N2 theo hình xoắn ốc.
Ví dụ: N = 5
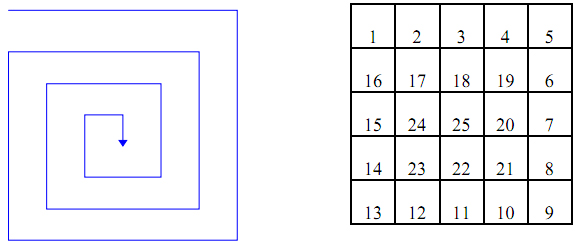
Bài 3: (8 điểm) Chọn đội tuyển Olympic
Kết quả thi đấu quốc gia của N vận động viên (đánh số từ 1 đến N) trên M môn (đánh số từ 1 đến M) được đánh giá bằng điểm (giá trị nguyên không âm). Với vận động viên, ta biết điểm đánh giá trên từng môn của vận động viên ấy. Các điểm này được ghi trong File văn bản có cấu trúc:
+ Dòng đầu ghi số vận động viên và số môn.
+ Các dòng tiếp theo, mỗi dòng ghi các điểm đánh giá trên tất cả M môn của một vận động viên theo thứ tự môn thi 1, 2 ,.., M. Các dòng này được ghi theo thứ tự vận động viên 1, 2, .., N.
+ Các số ghi trên một dòng cách nhau một dấu cách.
Cần chọn ra K vận động viên và K môn để lập một đội tuyển thi đấu Olympic quốc tế, trong đó mỗi vận động viên chỉ được thi đấu 1 môn (1<=K<=M,N), sao cho tổng số điểm của các vận động viên trên các môn đã chọn là lớn nhất.
Yêu cầu:
Đọc bảng điểm từ 1 File văn bản (Tên File vào Từ bàn phím), sau đó cứ mỗi lần nhận một giá trị K nguyên dương từ bàn phím, chương trình đưa lên màn hình kết quả tuyển chọn dưới dạnh K cặp (i,j) với nghĩa vận động viên i được chọn thi đấu môn j và tổng số điểm tương ứng với cách đã chọn. Chương trình kết thúc khi nhận được giá trị K=0.
Các giá trị giới hạn 1<=M,N<= 20
Download tài liệu để xem thêm chi tiết
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây: