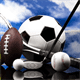Download.vn Học tập Lớp 10

Bài toán thực tế quy về hệ bất phương trình bậc nhất 2 ẩn Tài liệu ôn tập môn Toán lớp 10

Giới thiệu Tải về Bình luận
  • 2

Bài toán thực tế quy về hệ bất phương trình bậc nhất 2 ẩn gồm 22 trang hướng dẫn giải các dạng toán thực tế quy về hệ bất phương trình bậc nhất 2 ẩn. Mời các bạn tham khảo bài viết dưới đây.

Bài toán thực tế quy về hệ bất phương trình bậc nhất 2 ẩn

4 | P a g e N g u y ễ n B á H o à n g _ Đ T : 0 9 3 6 . 4 0 7 . 3 5 3
Bài toán Quy hoạch tuyến tính
A. Nội dung kiến thức.
1. Bất phương trình bậc nhất hai ẩn.
Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là:
(1)ax by c
, Ngoài dạng bất phương
trình (1) còn có các dạng
, , .ax by c ax by c ax by c
Trong đó
,,abc
là các số thực, a và
b không đồng thời bằng 0, x và y là các ẩn số.
Biểu diễn tập nghiệm của bất phương trình bậc nhất hai ẩn: Trong mặt phẳng toạ độ Oxy, tập hợp
các điểm có toạ độ thoả mãn bất phương trình (1) được gọi là miền nghiệm của nó.
Các bước biểu diễn miền nghiệm của bất phương trình
ax by c
(tương tự với bất phương trình
).ax by c
Bước 1: Trên mặt phẳng toạ độ Oxy vẽ đường thẳng
:.d ax by c
Bước 2: Lấy một diểm
00
( ; )M x y
không thuộc đường thẳng d.
Bước 3: Tính
00
ax by
và so sánh
00
ax by
với c.
Bước 4: Kết luận:
Nếu
thì nửa mặt phẳng bờ d chứa M là miền nghiệm của bất phương
trình
.ax by c
Nếu
00
ax by c
thì nửa mặt phẳng bờ d không chứa M là miền nghiệm của bất
phương trình
.ax by c
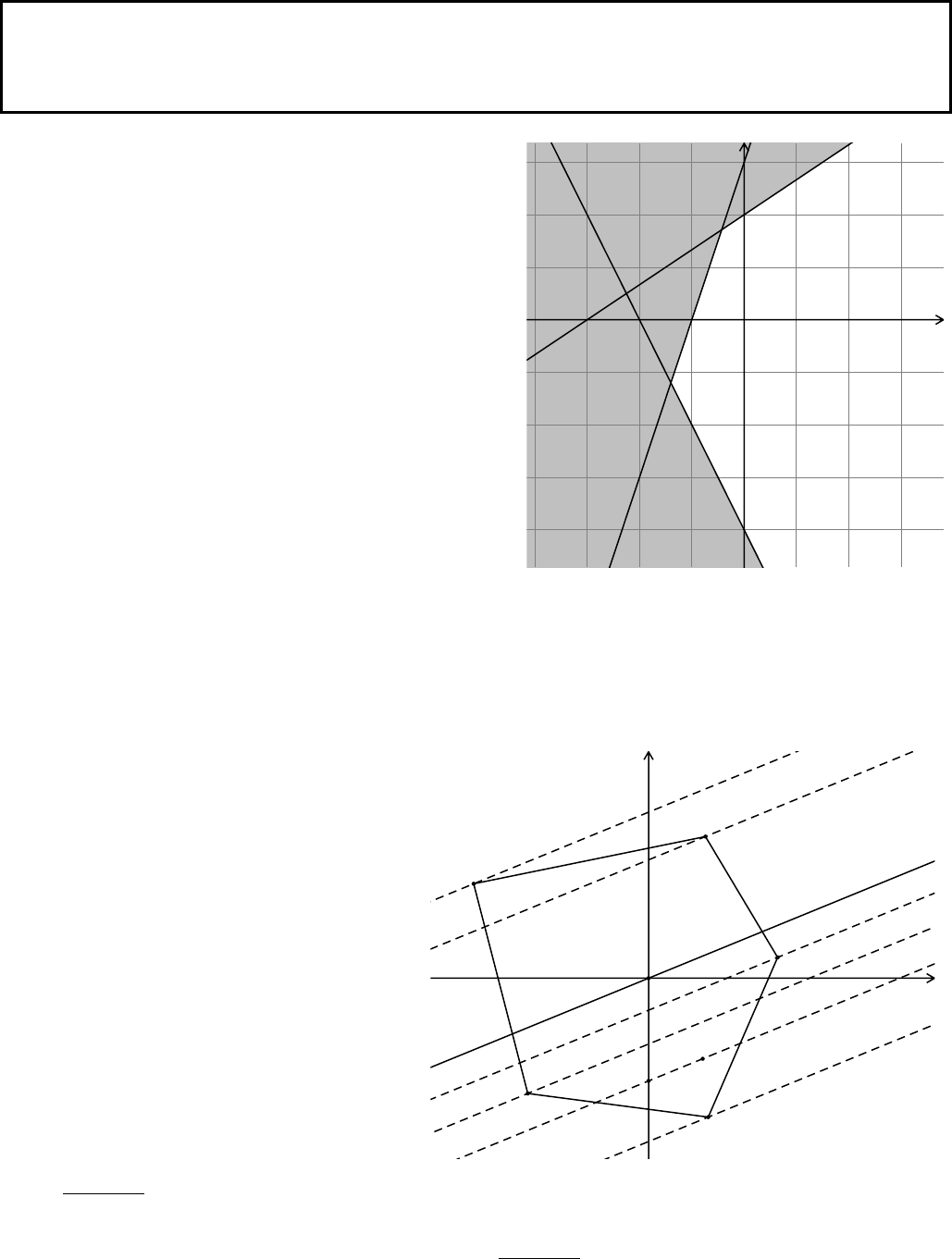
Ví dụ. Biểu diễn hình học tập nghiệm của bất phương trình bậc nhất hai ẩn
2 3.xy
Lời giải
Vẽ đường thẳng
:2 3.d x y
Lấy điểm M là gốc toạ độ O.
Ta thấy
Od
và
2.0 3 3
nên nửa mặt phẳng bờ d chứa gốc
toạ độ O là miền nghiệm của bất phương trình đã cho (miền không bị
tô đậm trong hình bên kể cả biên).
2. Hệ bất phương trình bậc nhất hai ẩn.
Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn x, y mà ta phải
tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương
trình đã cho.
Để biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn, ta thực hiện theo các
bước sau:
Bước 1: Vẽ tất cả các đường thẳng ứng với mỗi bất phương trình trong hệ bất phương trình
đã cho lên cùng một hệ trục toạ độ.
Bước 2: Xác định miền nghiệm của từng bất phương trình trong hệ phương trình đã cho
(bằng cách gạch chéo hoặc tô đậm phần không nằm trong miền nghiêm) trên hệ trục toạ độ
y
x
O
(Bài toán thực tế quy về hệ bất phương trình bậc nhất 2 ẩn)
5 | P a g e N g u y ễ n B á H o à n g _ Đ T : 0 9 3 6 . 4 0 7 . 3 5 3
ban đầu. Phần không bị tô đậm hoặc gạch chéo chính là miền nghiệm của hệ bất phương
trình đã cho.
Ví dụ. Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn
3 3 0
2 3 6 0 ( ).
2 4 0
xy
x y I
xy
Lời giải
Trước hết ta vẽ ba đường thẳng:
1
( ):3 3 0;d x y
2
( ): 2 3 6 0;d x y
3
( ):2 4 0.d x y
Thử trực tiếp thấy
(0;0)
là nghiệm của cả ba bất
phương trình trong hệ bất phương trình đã cho. Điều này
có nghĩa là gốc toạ độ thuộc cả ba miền nghiệm của cả
ba bất phương trình của hệ (I).
Sau khi bỏ các miền nghiệm không thích hợp,
miền không bị tô đậm trong hình bên (kể cả biên) là miền
nghiệm của hệ (I).
3. Bổ đề.
Cho biểu thức
( , )f x y ax by
, (a, b là các số thực không đồng thời bằng 0), trong đó
( ; )xy
là
toạ độ của các điểm thuộc miền đa giác
12
...
n
A A A
thì giá trị lớn nhất (nhỏ nhất) của
( , )f x y
(xét trên miền
đa giác đã cho) đạt được tại một trong các đỉnh của miền đa giác trên.
Chứng minh
Tác giả sẽ chứng minh trong trường
hợp
5n
và
0b
(các trường hợp còn lại xét
tương tự).
Giả sử
00
( ; )M x y
là một điểm đã cho
thuộc miền đa giác.
Qua điểm M và mỗi đỉnh của đa giác,
kẻ các đường thẳng song song với đường
thẳng
0.ax by
Trong các đường thẳng song song với
đường thẳng
0,ax by
đường thẳng
qua
M có phương trình
00
( ) ( ) 0a x x b y y
00
0.ax by ax by
Đường thẳng
cắt trục tung tại điểm
00
0; .
ax by
N
b



Vì
0b
nên
00
ax by
lớn nhất (nhỏ nhất) khi
00
ax by
b
lớn nhất (nhỏ nhất).
Quan sát hình vẽ bên ta thấy
( ; )f x y
lớn nhất khi
( ; )xy
là toạ độ của điểm
1
A
và bé nhất khi
( ; )xy
là toạ độ của điểm
4
.A
ax + by
= 0
A
5
A
4
A
3
A
2
A
1
N
M
y
x
O
(
d
3
)
(
d
2
)
(
d
1
)
y
x
O
6 | P a g e N g u y ễ n B á H o à n g _ Đ T : 0 9 3 6 . 4 0 7 . 3 5 3
Như vậy để tìm giá trị lớn nhất (nhỏ nhât) của biểu thức
( ; )f x y
trên miền nghiệm của một hệ bất
phương trình ta làm như sau:
Bước 1: Xác định miền nghiệm của hệ bất phương trình đã cho.
Bước 2: Tính các giá trị của hàm số
( ; )f x y
với
( ; )xy
là toạ độ các đỉnh của miền nghiệm.
Bước 3: So sánh các giá trị vừa tính được với nhau, giá trị nào lớn nhất (nhỏ nhất) là giá trị
lớn nhất (nhỏ nhât) của
( ; )f x y
trên miền nghiệm của hệ bất phương trình đã cho.
Ví dụ. Cho hệ bất phương trình
20
3 2.
0
xy
xy
x

Tìm giá trị lớn nhất của hàm số
( ; ) 2 3f x y x y
trên
miền nghiệm của hệ bất phương trình đã cho.
Lời giải
Chúng ta tìm được miền nghiệm của hệ bất phương
trình đã cho là phần không tô đậm trong hình vẽ bên (kể cả
biên).
Như vậy miền nghiệm là tam giác ABC (kể cả biên).
Toạ độ của điểm A là nhiệm của hệ phương trình:
20
42
;.
32
55
xy
A
xy




Toạ độ của điểm B là nghiệm của hệ phương trình:
Ta sẽ tính các giá trị của
( ; )f x y
với
( ; )xy
là toạ độ của các đỉnh
, , .A B O
4 2 4 2 2
; 2. 3. .
5 5 5 5 5
f
(0;0) 2.0 3.0 0.f
22
0; 2.0 3. 2.
33
f
Suy ra giá trị lớn nhất của
( ; )f x y
bằng 2 khi
2
( ; ) 0; .
3
xy




Vậy giá trị lớn nhất của hàm số
( , ) 2 3f x y x y
trên miền nghiệm của hệ bất phương trình đã
cho bằng 2 khi
2
( ; ) 0; .
3
xy




Lưy ý: Các kiến thức mà tác giả vừa nêu là các kiến thức cốt lõi để giải quyết các bài toán Quy
hoạch tuyến tính. Tuy nhiên bài toán Quy hoạc tuyến tính lại không cho ta cụ thể hệ bất phương trình và
hàm số
( , )f x y
như trong ví dụ trên mà chúng ta phải thiết lập thông qua các dữ kiện của bài toán.
B
A
y
x
O
xy 32
2

B 0;

.
x 0
3

Chia sẻ bởi: 👨 Trịnh Thị Thanh
Mời bạn đánh giá!
Liên kết tải về

Link Download chính thức:

Tìm thêm: Toán 10

Có thể bạn quan tâm

Xem thêm
Sắp xếp theo
👨

    Mới nhất trong tuần